稳 中求新 促进评价——浙江省2010年高中数学会考简析

●张金良 (浙江省教育厅教研室 浙江杭州 310012) ●梅红卫 (台州市第一中学 浙江台州 318000)●沈虎跃 (镇海中学 浙江宁波 315200)

稳 中求新 促进评价
——浙江省2010年高中数学会考简析

●张金良 (浙江省教育厅教研室 浙江杭州 310012) ●梅红卫 (台州市第一中学 浙江台州 318000)●沈虎跃 (镇海中学 浙江宁波 315200)

1 考试总体情况分析

在浙江省会考证书办会室的领导下，浙江省共有276 053人参加了2010年1月的高中数学会考，比2009年减少了17 447人，其中温州市有48 014人参加了会考，远多于其他各市．全省平均分为76．25，及格率为97．12%，标准差为11．42，难度为0．763，信度为0．77．A 等切分线为 85 ～100，占24．35%;B 等切分线为 77 ～84，占 30．84%;C等切分线为51～76，占41．92%;E等切分线为0～50，占2．88%．

平均分列全省前10名的县市区有:宁波镇海区、宁波鄞州区、绍兴上虞市、宁波北仑区、嘉兴海盐县、嘉兴秀州区、舟山普陀区、宁波大榭区、金华义乌市、绍兴市辖区，其中前10名的县市区中宁波占4个，绍兴占2个，嘉兴占2个，金华和舟山各占1个．

A等率列全省前10名的县市区有:宁波镇海区、舟山市辖区、嘉兴秀州区、绍兴市辖区、绍兴上虞市、宁波鄞州区、金华东阳区、舟山普陀区、宁波北仑区、嘉兴海盐县，其中宁波占3个，绍兴、嘉兴、舟山各占2个，金华占1个．

值得一提的是宁波市有24所学校的A等率超过了40%．

及格率最高的是宁波镇海区、宁波大榭区、舟山嵊泗县，均为100%;宁波北仑区的及格率为99．66%，位居第 4;嘉兴海盐县的及格率为99．62%，位居第5;及格率前10名的县市区的及格率都在99%以上，宁波占4个．另外，本次会考中共有16个县市区的及格率在99%以上．这16个县市区中，宁波占5个，嘉兴占3个，金华、绍兴、舟山各占2个，丽水、台州各1个．并且从大市看，整个嘉兴市的及格率最高，达98．91%．本次会考中共有85所学校的及格率低于90%．

会考平均分数60分以下的学校有37所，其中40分以下的有4所，40～50(不含50，下同)分的有7所，50～60分的有26所．

E等率达80%以上的学校有3所，70% ～80%的学校有3所，60% ～70%的学校有3所，50% ～60%的学校有3所，40% ～50%的学校有4所，30% ～40%的学校有6所．

从会考成绩的一些数据可以看出，全省的高中数学教学水平存在明显的差异，值得各部门重视．

2 试卷分析

2010年浙江省高中数学会考试题充分体现了《普通高中数学课程标准(实验)》(下称《课程标准》)和《浙江省普通高中新课程实验第一阶段数学学科教学指导意见》(下称《学科教学指导意见》)以及《浙江省会考标准》(下称《会考标准》)的要求，试题注重对新课标要求的空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力、应用和创新能力以及各内容领域的基础知识的考查．试卷立意新颖、结构合理、入口较浅、由易到难，有利于学生的考场发挥．试卷既突出了基础性，又重视数学能力的考查，注重数学思想方法的考查，对高中数学教学有很好的指导作用．整份试卷主要有以下特色:

(1)试卷命制突出有效性和技术性原则．试题内容效度高，注重试题的思维含量，鼓励学生创新，发展个性、发挥创造性，切实减轻学生负担．试卷结构简约、合理，题量、题型、题值、题序的设计与编制合理;试题的难度分布与区分度适宜，信度较高．

(2)试卷仍保持2009年的结构，分卷Ⅰ、卷Ⅱ两部分，卷Ⅰ为选择题，选择题仍为30题，满分为70分;卷Ⅱ为非选择题，其中填空题5题，满分为10分，解答题为3题，满分为20分，全卷满分为100分．选择题总体体现基础性的要求，第6，10，14，16，23，25 题在命题构思上有一定新意，第 25题要求具有较高的阅读理解能力，第26题要求学生具有综合解决数学问题的素质，第27～30题采用一卷文、理科分叉形式．对于分叉的试题，力求既关注文科与理科学生在学习内容上的差异，又体现水平考试的公平性．填空题的层次和梯度明显，第39题富有新意，解答题的背景分属3个不同模块，设计较合理，第41，42题题目简短，2个小题难度层次分明，分类讨论思想突出．在试题形式上力求图文并茂，为考查学生多种能力提供载体．试卷能根据会考标准要求命题，题型、题量、分值与会考标准一致，格式规范．

(3)试卷在知识点分布上，坚持全面与重点结合的原则，试题设计既立足于数学主干知识，又有相当的覆盖面．本份试题共42题，考查知识条目有54个，涉及必修1至必修5、选修系列ⅠA(其中侧文学生为必修1+选修系列1，侧理学生为必修1+选修系列2)各章节，并对重点章节内容进行重点考查．

(4)试卷在难度控制上遵循了《学科教学指导意见》中的基本要求和《会考标准》．整卷难度要求适当，符合学生的实际水平．在试题命制上注重既来源于课本，又重视创新．整卷在能力要求方面既注重对基础知识、基本技能掌握和基本思想方法的考查，又注重数学应用、探究试题的设计，以及注重数学理性思维能力的考查．42个试题的难度分布如表1所示．

表1 试题难度分布表

试卷在数学语言和文字规范上表述简洁、清晰，数学语言、符号使用规范严谨．

本份试卷充分体现了新的课程理念，试题注重新颖性．选择题采用一卷文、理科分叉形式，充分体现了新课程“数学基础性、思想性、应用性”的理念和自主探究的学习要求，立足培养学生的学习潜能，对此2010年命题组在上一年成功转型的基础上又作了新的探索，更加注重中学数学基本概念的本质含义和基本技能的培养．譬如:第6题深刻考查了不等式解的含义，第10题主要考查了等比数列概念，而不设置迷惑干扰支，第14题深刻考查了偶函数概念的理解，第23，25题要求学生关注数学应用，掌握基本的阅读理解能力，充分体现基础性、应用性，同时命题的设置充分体现了背景的公平性;第26，30，34，39题要求学生在理解掌握基本知识和方法的同时学会自主探究;第41题在利用导数研究函数单调性问题的形式上进行了新的尝试，问题简约，函数似曾相识，又是新的研究对象，研究方向明确，又要有一定的数学功底．同样，第42题以圆的切线为背景，通过中点弦、对称，用解析法研究直线与二次函数图像的关系，熟悉的情境和不同的呈现方式，让学生综合运用所学的知识去解决问题，能较真实地反映不同层次学生的学业水平．试题注重创新，压轴题既在会考命题范围内，又考虑优秀生应培养的严谨、深刻的数学思维，整卷区分度较好．

3 典型试题分析

2010年试题中有不少着眼于基本概念、知识和能力并重、构思新颖的问题，譬如第6，10，14，22，23，25，34，38，39，41，42 题都是能引起师生共鸣的题目．下面选择几例加以分析．

例1若函数f(x)=(x+1)(x－a)是偶函数，则实数a的值为 ( )

A．1 B．0 C．－1 D．±1

本题的平均分是1．74分，难度系数是0．87，区分度是0．46，正确选项是A．本题主要考查对偶函数的理解，既可通过偶函数的定义得到答案，又可从f(－1)=f(1)加上直接验算得到答案，很有创新性和区分度．

例2图1是某程序框图，若执行后输出的y值为0，则输入的x值不能是 ( )

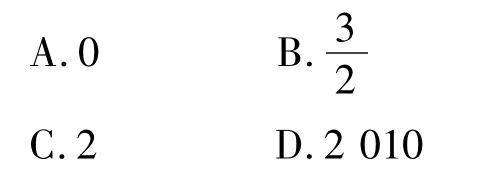
图1

本题的平均分是2．89分，难度系数是 0．96，区分度是 0．13，正确选项是B．主要考查程序框图的理解，可以通过逐步叠代计算，再通过归纳得到一般规律，从而获得答案．

例3若将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题，则该命题称为“可换命题”．下列4个命题:

①垂直于同一平面的2条直线平行;

②垂直于同一平面的2个平面平行;

③平行于同一直线的2条直线平行;

④平行于同一平面的2条直线平行．

其中是“可换命题”的是 ( )

A．①② B．①④ C．①③ D．③④

本题的平均分是2．32，难度系数是0．77，区分度是0．81，正确选项是C．本题主要考查对线面和面面关系的理解和掌握，同时考查命题变换和空间想象能力．通过对给出的几个命题的比较和判断而得到答案．

例4用餐时客人要求:将温度为10℃、质量为0．25kg的同规格的某种袋装饮料加热至30℃ ～40℃．服务员将 x袋该种饮料同时放入温度为80℃、质量为2．5kg的热水中，5分后立即取出．设经过5分后饮料与水的温度恰好相同，此时，m1kg该饮料提高的温度Δt1℃与m2kg水降低的温度Δt2℃满足关系式:m1× Δt1=0．8 ×m2× Δt2，则符合客人要求的x可以是 ( )

A．4 B．10 C．16 D．22

本题的平均分是1．81，难度系数是0．60，区分度是1，正确选项是C．本题主要考查学生的阅读理解和数学模型处理能力，培养应用意识，通过必要的计算和比较可以得到答案，有一定的实用性和区分度．

本题的平均分是0．87，难度系数是0．29，区分度是1，正确选项是B．本题是对线性规划问题的综合考查，主要目的是考查学生的数形结合、分类讨论等综合解题能力，在一定的计算支持下创造性地取得问题的解决，能全面反映学生的数学素养，也有相当高的区分度．

图2

例6函数f(x)=ax3+bx2+cx+d(a，b，c，d∈R)的图像如图2所示，则下列结论中正确的是 ( )

A．c＞0 B．a+b＞0

C．d ＜0 D．3a+b=0

本题的平均分是2．01，难度系数是0．67，正确选项是D．本题是从函数解析式、图像出发，综合考查学生信息处理、数形结合、分类讨论等综合解题能力，立足基本概念和方法，全面反映学生对函数、导函数的理解和掌握的水平，也有一定的难度和区分度．

例7若棱长为a的正方体的表面积等于一个球的表面积，棱长为b的正方体的体积等于该球的体积，则 a，b 的大小关系是＿＿ ．

本题的平均分是1．01，难度系数是0．51，区分度是1．主要考查正方体与球的表面积与体积计算．大部分错误的学生不能按照题目要求写出a与b正确的大小关系:a＜b，而是写成了=或a＞b等．主要原因是没有理解大小关系的要求，记错或用错表面积、体积公式和不等关系的处理欠缺．本题有一定的新意，使部分阅读理解能力较弱和思路不清晰的学生出错，这也有待我们重视．

例8若不存在整数x满足不等式(kx－k2－4)(x－4)＜0，则实数 k 的取值范围是 ＿＿．

(1)若a=1，试判断并证明函数f(x)的单调性;

(2)当a∈(1，6)时，求函数 f(x)的最大值的表达式M(a)．

本题的平均分是2．81，难度系数是0．47，区分度是0．83．本题多层次地考查了函数的单调性、最值等基本性质和利用导数判断函数的单调性，属综合题．题目简短，2个小题难度层次分明，分类讨论思想突出，有一定的难度，且有较好的区分度．主要错解有:

图3

例10设点 P(m，n)在圆x2+y2=2上，l是过点P的圆的切线，切线l与函数y=x2+x+k(k∈R)的图像交于点A，B，点O是坐标原点(如图3)．

(1)若 k= －2，点 P恰好是线段AB的中点，求点P的坐标．

(2)是否存在实数k，使得以AB为底边的等腰△OAB恰有3个?若存在，求出k的取值范围;若不存在，请说明理由．

4 对今后教学的建议

4．1 加强学习，明确要求，提高效率

在会考复习时，首先要认真学习《课程标准》、《学科教学指导意见》和《会考标准》，只有研究与领会考什么、考多难、怎样考这3个问题的具体规定和解说，才能实现有效复习;同时还要结合不同学生的实际情况，制定适合学生个体的学习目标和计划;有时让学生通过例卷练习熟悉会考试卷的具体形式，例如题型及其数量和分值比例(选择题 ∶填空题∶解答题=70∶10∶20)，每种题型的解题要求、常用方法、解题步骤，以提高学生的学习兴趣，从而主动学习．

4．2 重视双基，落实练习，提升能力

会考是一项终结性水平测试，试题的难度并不大，但其特点是重基础、知识点覆盖面大，需要学生全面、系统、有针对性地认真复习．在教学中，教师要认真把握《会考标准》和《教学指导意见》的要求，切实抓好基本概念及其性质、基本技能的教学，要多方向落实对基本概念、定理、公式等的理解和掌握，譬如前提条件、结论、推导、变式、反面思考、类比等，让学生在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能，同时要注重对学生运算能力的培养，并形成合理的知识网络结构．对文科生和基础较差的学生，要重视基本技能的训练，采用灵活多样的教学方法，有效地提高学生对基础知识的识记和应用，掌握基本技能．此外，还要有目的、有计划地选择专项练习，以巩固和提高复习效果．

4．3 关注通法，淡化技巧，重视思想

在会考复习中通过系统整理通性通法，例如配方法、换元法、待定系数法、分析法、反证法、归纳法等，渗透常见的数学思想方法，例如函数方程、等价化归、数形结合、分类讨论等．通过不断积累，使学生学会解题，并逐渐内化为自己的经验，形成解决问题的自觉意识，提高复习效果．

4．4 强调规范，关注过程，培养思维

规范解答的表达过程是对学生的基本要求．俗话常说，表达的思路要清晰、条理要清楚、过程要简明，培养学生的数学表述能力是培养逻辑思维能力的一个重要方面．学生在答题中，由于书写表达不规范或是表述能力的欠缺，也是造成失分的原因．表述是一种重要的数学交流能力，因此，在教学中要重视训练、培养学生良好的数学表述能力．同时也要加强考前指导，学习《会考标准》中有关答题的要求，尽量减少由于表述不清造成的失分．

4．5 重视辨析，消除错理，正本清源

不管是知识技能传授，还是方法的掌握和数学思想的渗透，学生往往容易出错，因此，在会考复习时对知识性错误、逻辑性错误、策略性错误、过程性错误等进行分类纠正，从正、反、图、例等方面入手消除错误，正本清源，这样一定能使学生更加灵活、准确地运用数学知识和数学思想方法去分析问题和解决问题．