计算机辅助工程以弧长为参数的连续插值曲线的生成
刘花丽,郝艳莉
(1.郑州文理专修学院,郑州 450001;2.河南职业技术学院,郑州 450046)
0.引言
1946年 Schoenberg提出样条函数的概念,为解决曲线之间的连续问题提供了可能。参数样条曲线曲面即用来描述几何形状的样条方法。1971年法国雷诺汽车公司的 Bezier提出一种由控制多边形设计曲线的 Bezier参数曲线方法。1972年,de Boor在总结前人经验的基础上给出了 B样条参数方法,该方法发展成为应用广泛的B样条曲线。因此可知参数的选择对曲线的生成是极其重要的。从曲线论出发,曲线的曲率是曲线的内在几何量,曲率的大小代表着曲线的弯曲程度;曲线的弧长变量是曲线的几何不变量,它有助于实现快速、准确的时空变换。因此在 GCAD中,诸如机械加工中刀具的移动,机器人沿某一轨道运动或沿曲线等弧长分布铆钉等实际工作中都提出了参数曲线的弧长参数化,即以曲线自身不变量的弧长为参数建立的方程。在文献[1]、[2]中,以近似弧长为参数,这些方法实际上仍是采用一般参数作为变量建立方程的,并没真正的实现弧长参数化。在文献[3]、[4]、[5]中真正实现了弧长参数化。其中 [3]仅做到了 G1连续。从其建立曲线方程可以看出他们是一组非线性方程组;对于求非线性方程组的解来说并不像线性方程组求解那样有一套成熟的理论来支持它,只能靠数值方法来解决它,并且针对个别问题只能做个别处理。计算机计算速度的提高为数值算法提供了有力的保障,为实现真正的弧长参数化提供了求解工具。
数值方法为计算方法提供了有力的保证,所以弧长参数在曲线插值中的应用越来越被看好。本文在文献[3]的基础上,将其推广到 G2连续,并给出了其数值解的求解方法。
1.平面曲线
将平面曲线看成曲线的挠率为零的空间曲线来进行研究,因此讨论以平面曲线为主。但是平面曲线有它自身的特殊性。利用平面曲线的特殊性质,由曲线的相对曲率和平面曲线的 Frenet公式 (见参考文献[6]、[7])得到以下定理。
平面曲线基本定理:设κ(s)为曲线 P(s)的曲率,α(s)为单位切向量,θ(s)为α(s)与 x轴正向夹角,则有:
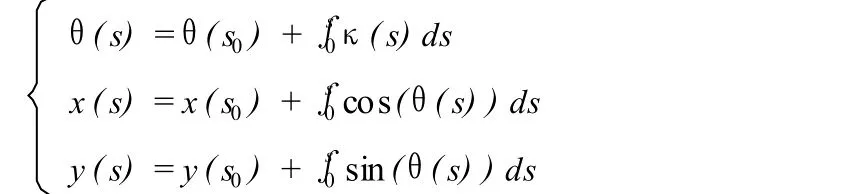
为了方便其见,将曲线的曲率记为κ,则κγ=±κ,其中“+”表示单位切向量β正好指向曲线弯曲的一侧,而“-”表示单位切向量β指向曲线弯曲的一侧。以下讨论中曲率的正负都与此处相同。
对曲线 P=P(s)在 [a,b]上的插值来说,只需对 [a,b]进行划分:a<s0<s1<…<sn<b。对∀s∈[si,si+1]有:
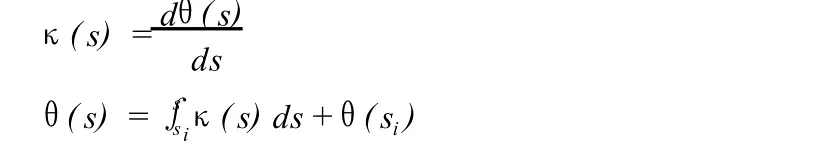
所以整条插值曲线可以写成:
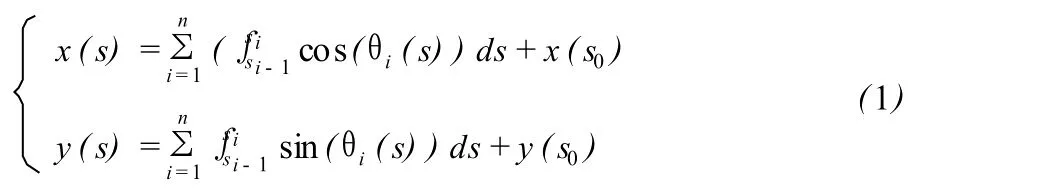
下面讨论利用 (1)式生成 G2连续的曲线方程。
2.G2连续曲线
文献[3]指出在平面点列间插值,利用已知点的坐标和切线角,根据平面曲线基本定理,反求两端点处的曲率,在线性曲率条件下生成的曲线只达到了 G1连续。下面通过适当的加入一些假设前提条件更进一步地利用平面曲线定理,得到的插值曲线达到 G2连续。
2.1 分段线性曲率插值曲线
在平面上任给定一组型值点{Pi}n0,型值点端点处的曲率为{κi}n0。通过这些型值点建立一条 G2连续的曲线。根据几何样条曲线的定义,在每两个型值点之间是一段 cornuqu螺线 (参考文献 [8]),并在整个样条上 G2连续。因此在每两个型值点之间做曲率关于弧长参数的线性插值。为此首先考虑在两个型值点间进行曲线插值,为了保持符号简洁,可以再次省略指标 i;而用 P1、P2代表任意相邻的两个型值点。设曲线在 P1点的切线角为θ1,曲率为κ1;在 P2点的切线角为θ2,曲率为κ2。为得到一条 G2的曲线,由参考文献[3]知,直接引用 (1)对于任意的初始角不一定能得到一条 G2连续曲线。所以在已知条件下,再引入新的变量,使得对于给定的θ1、θ2,可以得到一条满足条件的 G2连续曲线。假定过此曲线上 P1、P2之间有一自由点 Q,且 Q处的曲率为任意可变的,记点 Q处的曲率为κ。则把 P1、P2之间分成两段,对每一段作线性插值,则在 P1、P2之间分段进行曲率线性插值。设 P1Q间的弧长为 s1,P2Q间的弧长为 s2且 P1,P2在一条水平线上 (即设 P1,y=p2,y)。
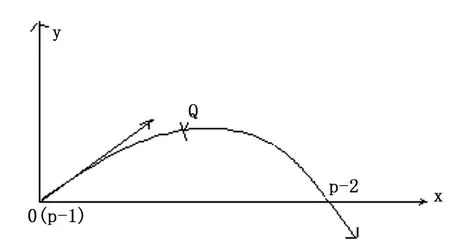
图 1 插值曲线 (单位化的图示)
第一段曲线 P1和 Q之间的曲率κ1(s)为线性变化:
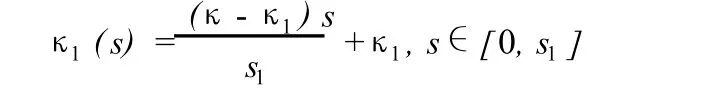
则其切线角为:
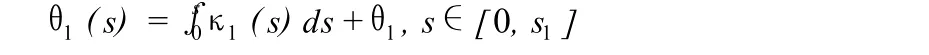
P1和Q之间的一段 Cornuqu螺线在局部坐标系中被表示为关于弧长 s的参数方程,当积分上限为 s1,就得到 Q出的坐标设为 (x1,y1),则

第二段曲线:与第一段曲线生成相似。
设 Q和 P2之间的曲率κ2(s)为线性变化:
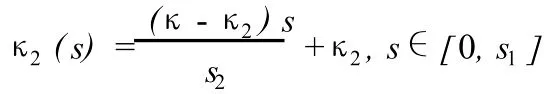
则其切线角为:
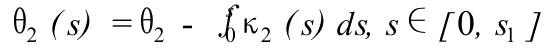
P2和Q之间的一段 Cornuqu螺线在局部坐标系中被表示为关于弧长 s的参数方程,当积分上限为 s2,就得到 Q出的坐标设为 (x2,y2),则
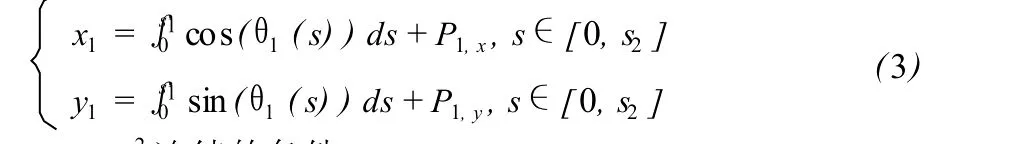
2.2 G2连续的条件
满足上述条件的解有很多,为了保证插值曲线 G2连续,需要在连接点处加入切线连续的条件。由弧长为参数的曲线切向量为单位切向量知,要讨论曲线在一点处的连续性,只需要讨论在此点处的切线方向平行;而切线方向平行有两种情况:一种是方向相同,一种是方向相反。如果切线方向相反时,构成在 Q处左右两端曲率互为相反数,所以不会满足 G2连续条件。因此只考虑方向相同的情形。切线方向相同即切线角相等,则在 Q处满足:

又因为 Q在一个坐标系下的坐标是唯一的,则由 (2)和(3)得

(4)、(5)就是曲线 G2连续的条件。由 (4)和 (5)得在 Q点处 G2连续满足以下方程:
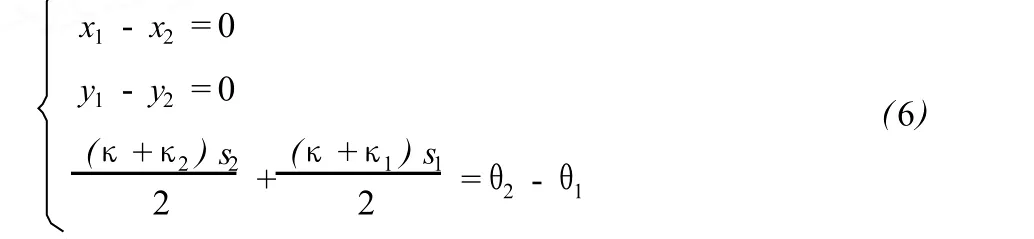
将 x1,x2,y1,y2代入上式即得:
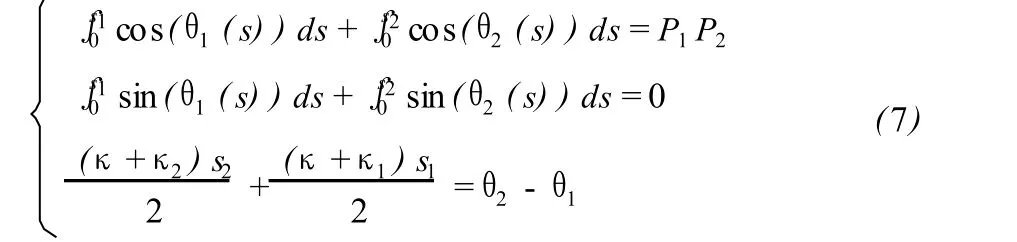
得到整条曲线的插值曲线方程:
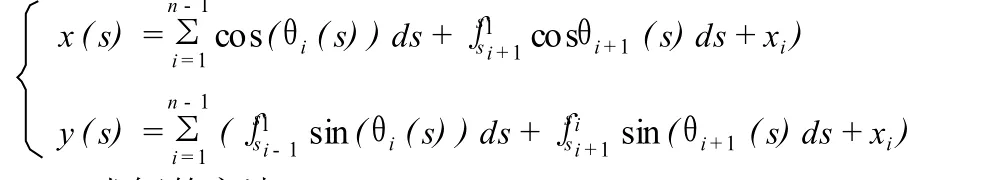
2.3 求解的方法
对于线性方程组的求解问题已经有它的一系列成熟的理论和方法,是非常方便的。但是关于 s1,s2,κ的方程组为非线性方程组;对于非线性方程来说没有成熟的理论来解决,只有借助于数值的方法来解决。所以解决这种非线性方程组,针对个别的问题作个别处理。对 (7)式要找出一种数值方法来求其方程组的解。
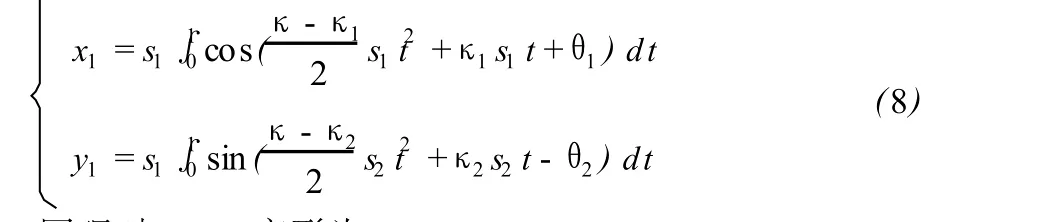
同理对 x2、y2变形为:
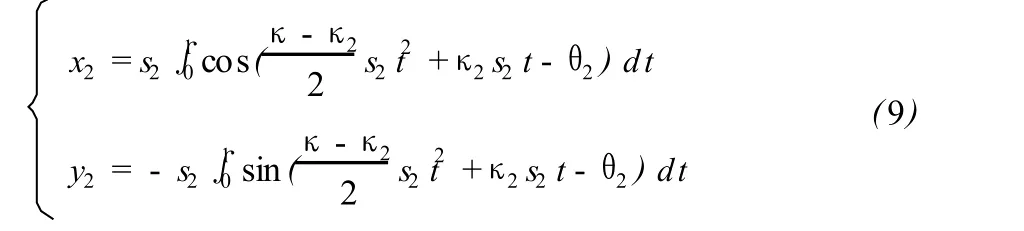
将 (8)和 (9)带入 (7)即得:

其中:
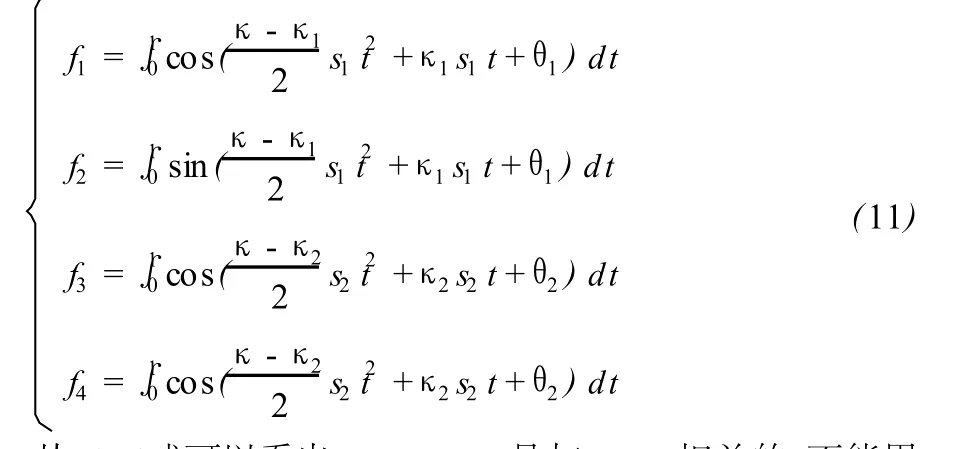
从 (11)式可以看出 f1,f2,f3,f4是与 s1,s2相关的,不能用非齐次的线性方程的理论来解决,只能借助于数值计算的方法来求解。不妨对 (7)式在给定任意初值的情况下,由计算机判断在迭代过程中 f1f4+f2f3是否为 0,求出方程组的解。
2.4 算法实现
由 (7)可得:

由 (7)中的第三个式子可得:
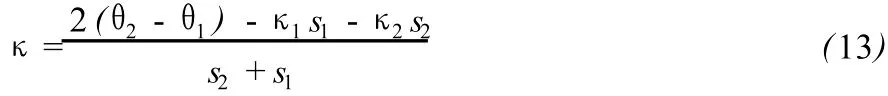
由 (12)和 (13)可以得以下的算法:
第一步:方程组变型为

得出
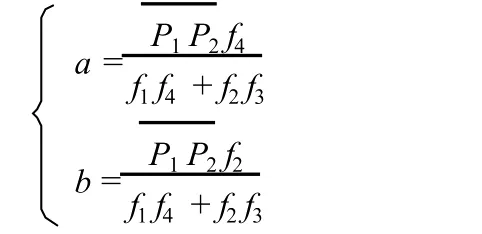
第二步:先给出 s1,s2的一个合适的初值;
第四步:把κ得值代入 (14),进行进行求解。若对任一个很小的给定正数δ,‖a-s1‖≥δ或‖b-s2‖≥δ,则 s1=a,s2=b;循环从第二步开始执行直到‖a-s1‖≥δ或‖as2‖≥δ时退出循环;若在迭代过程中出现了 f1f4+f2f3=0或 s1,s2互为相反数,说明此初始条件用此方法求解是无解的,退出循环。
第五步:求得的 a,b即为 s1,s2的值,并由 (8)求出;
第六步:将它们代入原始方程组进行画图,进行整体连接。
3.结论
本文从微分几何的观点入手,实现了弧长参数化,并把插值曲线从 G1连续推广到 G2连续;在分段线性曲率条件下得出插值样条生成过程和实现方法。在允许存在一定误差的范围内,利用数值方法求解,在单枝区间内求出的解总是适定的。从以上分析可以看出,在坐标系中讨论曲线的生成问题,不仅和两端的曲率有关,也和两端的切线方向有关。利用此方法做插值曲线的另一个好处是可以很方便地得出整条曲线的走势和曲线的弧长长度,曲线整体和局部的曲率变化;可以很方便的控制曲线的形状、走向,这是比其他插值方法的优越点。在工程上主要用于机床加工、工程测量和工程预算等方面。
[1]李东,李晓明.构造曲率法及其在曲线设计中的应用[J].计算机工程与建设,1996,17(1):47-53.
[2]Fang Kui,Cai Fang.C2Continuous Nearly Arc-length Parameterized Curve[J].Numerical mathematics,2003,12(2):143-149.
[3]蒋献峰,孙毅.平面曲线的曲率表示及其应用[J].计算机辅助设计与图形学学报,1999,11(5):464-466.
[4]吴家骥,杨东英.基于曲率数据的曲线拟合方法的研究[J].应用科学学报,2003,21(3):258-262.
[5]蒋献峰,孙毅.圆渐开线平面插值样条及应用 [J].计算机辅助与图形学学报,2001,12(8):708-711.
[6]陈维桓.微分几何初步 [M].北京:北京大学出版社,1990.
[7]梅向明,黄敬之.微分几何 [M].北京:高等教育出版社,2003.
[8]柳朝阳,周小平.计算机图形学 [M].西安:西安电子工业出版社,2005.

