宽幅矮塔斜拉桥最大悬臂阶段主梁受力分析

刘沐宇， 孙文会， 孙向东， 袁卫国

(1.武汉理工大学 道路桥梁与结构工程湖北省重点实验室， 湖北 武汉 430070；2.广东省公路勘察规划设计院， 广东 广州 510507)

矮塔斜拉桥起源于日本，是介于梁式桥和斜拉桥之间刚柔相济的新型桥型[1]。其斜拉索只分担部分荷载，还有相当部分的荷载由主梁的受弯、受剪来承受。这种桥型兼有斜拉桥和连续梁桥的特点，其主梁刚度较大，不仅受轴向压力，还要承担相当部分的弯矩和剪力[2]，空间应力的不均匀现象十分严重。随着矮塔斜拉桥跨径和主梁横向宽度的进一步增大，宽跨比和宽高比随之增大，剪力滞效应更加严重，施工过程中主梁截面剪力滞对结构的影响较成桥以后影响更大，施工过程中主梁截面的内力在某些工况下大于成桥状态的内力，使得施工内力成为控制截面设计的内力值[3]。一般的平面及空间杆系分析很难反映其实际的应力分布。所以有必要对宽幅主梁在最不利状态(即最大悬臂施工状态)下的空间受力状态进行空间仿真计算分析。

为了明确了解最大悬臂施工阶段的拉索区主梁的受力特性，本文以西江特大桥为研究背景，采用有限元理论，通过建立拉索锚固区梁段空间有限元模型，分析最大悬臂施工阶段的主梁空间受力状态。结果表明通过设置后浇段的施工方法在最大悬臂施工阶段主梁的受力状态合理，研究结果对同类型矮塔斜拉桥的设计和施工有一定的参考意义。

1 工程概况

江肇高速公路西江特大桥位于珠江三角洲西部地区，其主桥采用单索面四塔矮塔斜拉桥结构方案，跨径布置为128 m+3×210 m+128 m，桥塔高30.5 m。主梁采用变高度斜腹板单箱三室宽幅脊梁截面，主梁顶板宽38.3 m，在同类型桥梁中，其宽度位居世界首位。悬臂长8.15 m，两侧设5.15 m宽后浇带，箱梁后浇段滞后5个梁段(共20 m)浇筑。主塔根部梁高6.5 m，跨中梁高3.5 m，主梁的梁底曲线按1.8次抛物线变化。顶板板厚0.25 m，底板厚由跨中的0.3 m变厚至塔根部的1.0 m。主塔墩处塔梁墩固结，边墩设纵向活动的竖向支座。每个主塔各设16对拉索，梁上索间距4.0 m，塔上索距0.8 m，全桥共128根斜拉索。主梁立面及主梁横断面布置见图1和图2。

图1 西江特大桥立面布置/m

图2 主桥结构断面/cm

西江特大桥是世界上主梁最宽的矮塔斜拉桥，主梁宽度达到38.3 m，考虑到索力的纵向力按一定的角度方向向两侧传递[4]，在主梁中传递有滞后性和减轻宽幅主梁施工时剪力滞效应，该主梁两侧设5.15 m宽后浇带，箱梁后浇段滞后5个梁段(共20 m)浇筑。

2 空间有限元分析

2.1 最大悬臂状态主梁空间有限元模型

运用通用有限元软件ANSYS建立主梁最外侧12个索距(共48m) 节段有限元模型，对其在最不利状态(即最大悬臂状态)下的工况进行分析。主梁采用Solid95实体单元离散，主梁C60混凝土弹模E=36 GPa，泊松比0.167；预应力钢筋采用Link8单元模拟。为了准确模拟施工阶段的实际受力，主梁的后浇带通过模型的生死单元杀死(如图3所示)。预应力通过将钢绞线单元节点与离其最近的混凝土单元节点相耦合，并用降温措施模拟预应力的施加。

边界条件和荷载：模型近塔端方向截面固结，约束整个截面所有方向的位移和转角，另一端自由。在悬臂端的混凝土湿重和挂篮等荷载由空间杆系模型得到的内力加在远塔端截面上，计算中未考虑普通钢筋的影响。模型模拟了实际的斜拉索锚固区形状，将最大悬臂状态下索力作为均布面力加在钢垫板下区域，作用方向垂直于齿块锚固面并与拉索的方向一致。

对桥梁局部空间受力分析时，运用圣维南原理，采用空间杆系结构分析和三维实体结构分析相结合的方法[5]，即把用梁单元进行整体计算所得内力和位移作为局部切开处的外力和位移边界条件的方法，解决求解桥梁局部应力和变形状况问题。

图3 最大悬臂状态下主梁的空间有限元模型

表1 梁段截面的内力

2.2 计算结果与分析

2.2.1顶底板应力分布

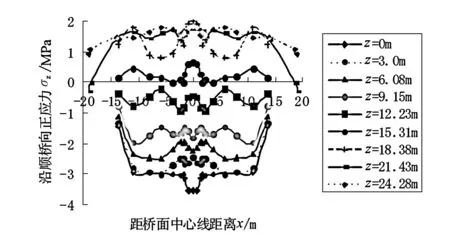
图4 主梁的上顶面纵桥向正应力分布

在最大悬臂施工阶段主梁的上顶板主要受拉，图4为主梁上顶面纵桥向正应力分布图。由图4可以看出，从悬臂端到近塔端，主梁的桥面正应力由受压逐渐变为受拉。虽然部分截面少部分区域的拉应力值偏大，但未超过混凝土抗拉强度设计值1.96 MPa。由于该分析是主梁在最不利状态下的最不利位置的内力，实际结构出现这种状态的机会很小。主梁翼缘板和中室上顶板正应力变化较大，其它区域的纵桥向正应力沿横桥向变化不大，但整体分布较均匀，且均在合理受力范围之内。沿顺桥向桥的纵桥向正应力变化不大，分布也较均匀。

由图5可以看出，主梁的下翼缘板受压，主梁沿桥的纵桥向正应力变化不大，整体分布较均匀。从悬臂端到近塔端，主梁的下底板纵向受压逐渐增大，主梁的纵向正应力沿桥的横向变化不大，整体分布较均匀，且在混凝土抗压强度设计值的合理范围内。计算结果表明通过在宽幅主梁施工过程中设置后浇段，后浇段滞后5个梁段浇注，主梁的顶底板正应力沿桥纵向和横向变化不大，剪力滞效应明显降低，顶底板受力均在合理范围之内。

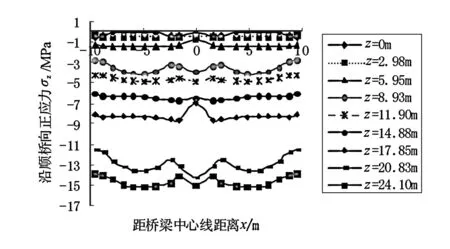
图5 主梁的下底面纵桥向正应力分布

2.2.2腹板应力分布

由图6和图7可以看出，边腹板的正应力最大压应力为12.2 MPa，最大拉应力为1.17 MPa，均在设计的容许范围之内，整体受力合理。边腹板和中腹板的纵向正应力沿桥的横向变化不大，整体分布较均匀。从悬臂端到近塔端，主梁的边腹板和中腹板远离上顶面端压应力逐渐增大，而靠近上顶面压应力逐渐减小，直至出现拉应力。腹板的纵桥向正应力随着远离上顶面基本成线性变化，中腹板上顶端区域由于靠近拉索作用锚固区，其正应力由于出现应力集中而改变了应力分布规律。远离上顶面端压应力逐渐增大是由于拉索不断地增多，索力不断增大而导致压应力增大；而靠近上顶面由于拉索的水平倾角不断增大而产生拉应力。

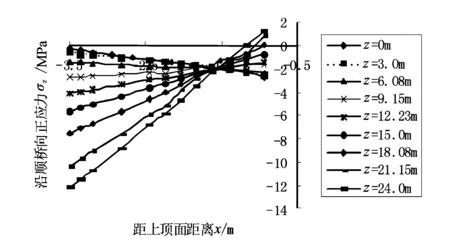
图6 主梁的边腹板纵桥向正应力分布

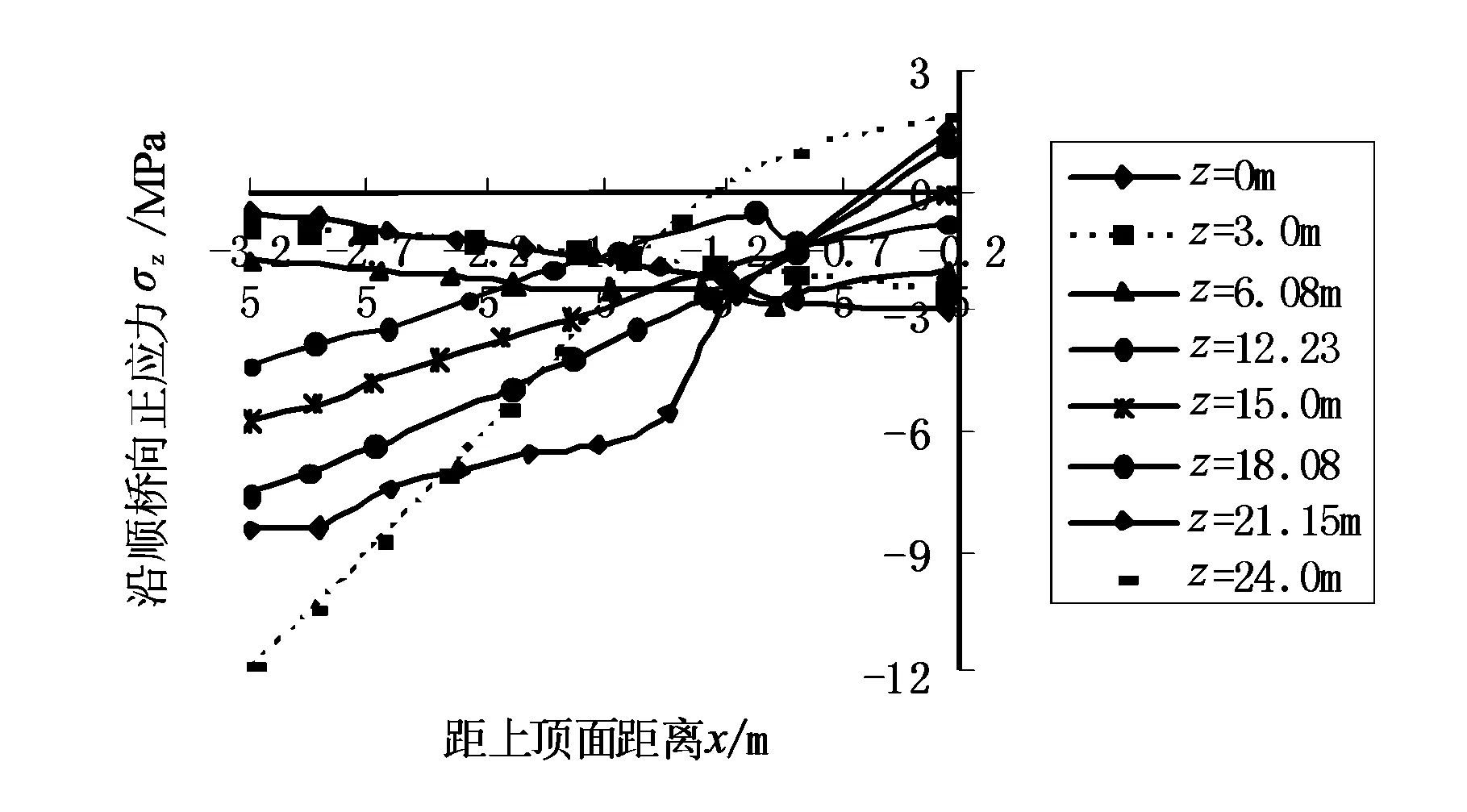
图7 主梁的中腹板纵桥向正应力分布

综上所述，由模型整体计算结果表明：该主梁在最大悬臂施工状态主梁的整体受力状态合理，应力分布比较均匀。应力较大值均出现在靠近悬臂端部、预应力锚点和拉索作用的锚固点，而离开该局部区域应力则很快减小并趋于均匀分布，它们是由应力集中现象引起的。在主梁的腹板和加劲肋的底缘也出现一定的拉应力，均小于1.5 MPa，它们由拉索拉力引起，但影响不大。在横隔板靠近锚固区区域由于拉索作用而存在纵向拉应力，实际结构通过适当的配筋加强，且锚头下有锚垫板等分散应力的措施，所以该梁段整体分布较均匀，在合理的受力范围之内。

3 结 论

通过建立索力作用的锚固区域梁段有限元模型，进行空间有限元分析，分析最大悬臂施工阶段的主梁空间受力特性，可以得到如下结论：

(1) 通过对12个索距(共48m)主梁节段在最不利状态(即最大悬臂状态)下的受力分析可知，除局部应力集中区域外，该拉索区梁段的应力均处于合理的范围。

(2)边腹板和中腹板的纵桥向正应力沿桥的横向变化不大，整体分布较均匀。从悬臂端到近塔端，腹板的纵桥向正应力随着远离上顶面而基本成线性变化。

(3)通过在宽幅主梁施工过程中设置后浇段，后浇段滞后5个梁段浇注，梁段的纵桥向正应力沿纵桥向变化不大，横桥向受力较均匀，整体分布较均匀，均在合理的受力范围之内。这样设计既能减轻宽幅主梁施工时的自重和剪力滞效应，又能使后浇段参与主梁的整体受力。因此，该桥的设计和施工方法合理。

[1]郑一峰, 黄 侨, 张连振. 部分斜拉桥结构体系分析[J].公路, 2005, (6): 1-5.

[2]蔺鹏臻, 黄卫东, 吴荔青. 部分斜拉桥箱梁横向应力分布[J]. 兰州铁道学院学报(自然科学版), 2002, 21(4): 46-49

[3]周 伟, 蒋益飞. 斜拉桥最大双悬臂施工阶段主梁剪力滞效应分析[J]. 公路, 2008, (6): 59-63

[4]美国各州公路和运输工作者协会(AASHTO).美国公路桥梁设计规范：荷载与抗力系数设计法 [M].辛济平等译.北京：人民交通出版社, 1998.

[5]郑振飞, 徐 艳, 陈宝春. 深圳北站大桥拱墩固结点局部应力分析[J]. 中国公路学报, 2000, 13(2): 69-72.

[6]JTG D62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范 [S].