火电厂预应力框架拟静力试验与推覆分析
彭自强, 葛 翔
(武汉理工大学 土木工程与建筑学院, 湖北 武汉 430070)
我国电力行业的快速发展,尤其是大容量机组的投入使用,对火电厂的土建设计和施工技术都提出了更严的要求。大机组主厂房结构不仅受力复杂、荷重大,而且平面和空间尺寸大、结构自重大。为满足使用要求,主厂房框架梁高普遍过大,导致“强梁弱柱”、底层柱轴压比超限、地震作用下柱端破坏突出、梁柱节点抗震性较差。目前我国采用的两阶段设防的设计方法,虽然能够从实践上满足抗震设计要求,但是却难以提供结构在地震作用下的整体反应,无法定量评估该类结构的抗震性能[1]。
拟静力试验是复杂结构抗震性能研究的重要手段。结合拟静力试验,采用静力弹塑性分析方法进行结构分析,既能模拟结构由弹性阶段到承载力丧失的整个过程,找出薄弱环节,又可以判断结构的抗震承载力及不同设防等级下的目标位移、层间位移角、各杆件受力状态。静力弹塑性分析方法在充分考虑结构的塑性特性的同时又比时程分析法简便。

图1 拟静力模型配筋
1 工程概况
本实验原型为火电厂煤仓间预应力框架,模型在框架平面内采用1∶8缩尺比例,平面外比例为1∶4。
试验模型混凝土等级为C45,普通纵向受力钢筋采用HRB335级钢筋,箍筋采用HPB235级钢筋,预应力筋采用1×7-15.20-1860级高强低松弛钢绞线,如图1所示。
以跨中弯矩等效为原则,将作用在结构上的荷载等效为多组集中荷载。由于结构的主要恒活载集中于一、二两层,变形以剪切变形为主,因此侧向荷载根据振型分解法求得等效水平作用力施加于结构上,如图2所示。
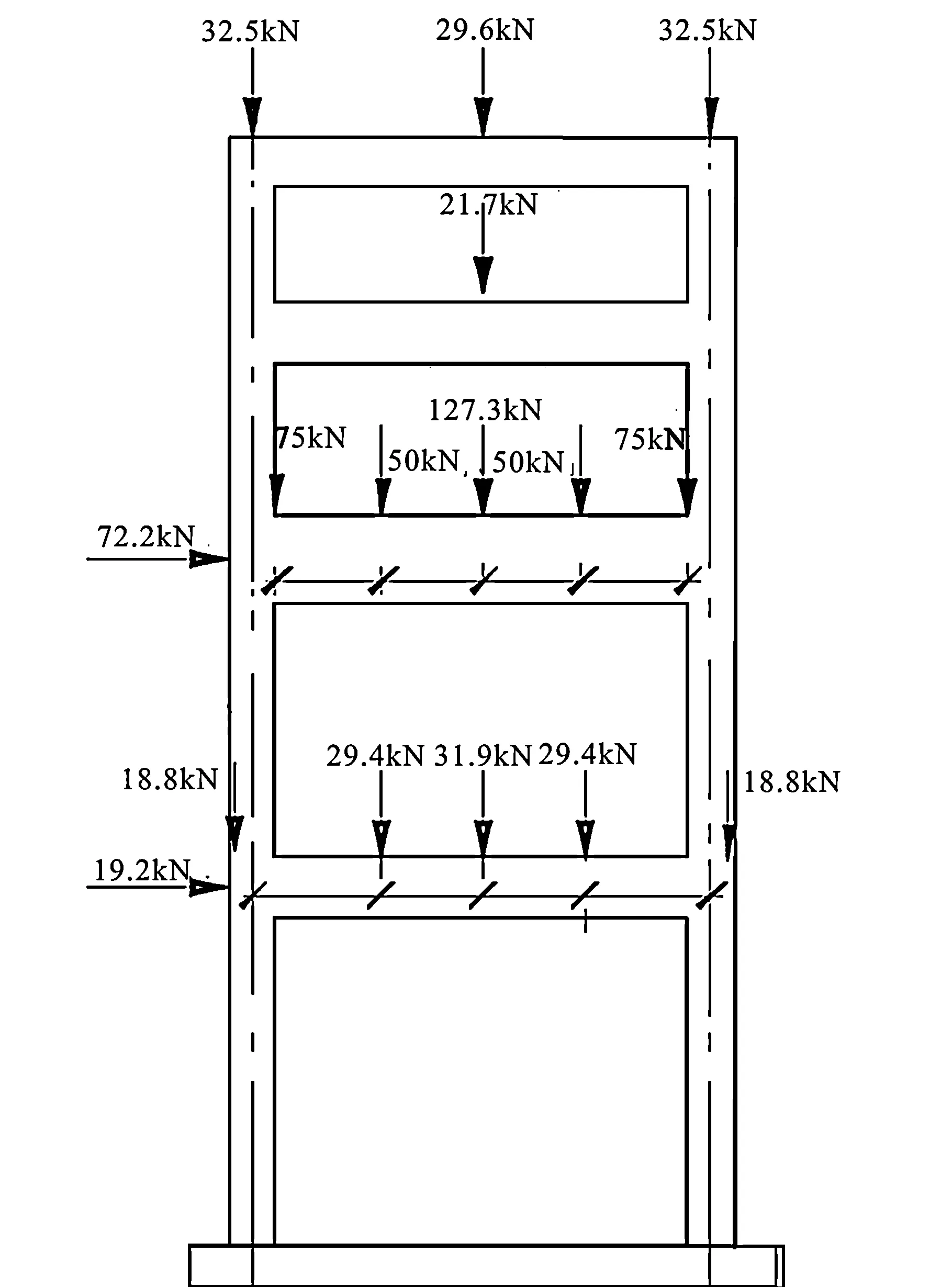
图2 试验荷载
2 分析模型
2.1 分析方法
静力弹塑性(Push-Over)分析方法是一种静力非线性计算方法,采用逐级单调施加模拟地震水平惯性力的侧向力,对结构进行静力单调加载下的弹塑性分析。这种方法不但能考虑结构的弹塑性特征,又将设计反应谱引入了计算过程和计算成果的解释[2~4]。
2.2 铰属性
SAP2000软件采用的静力弹塑性分析方法是美国ATC-40规范的能力谱法,铰属性定义如图3所示。其中B点代表屈服(出现塑性铰)、CP为预防倒塌点,C为倒塌点,各性能点所对应的横坐标为相应的弹塑性位移限值[5,6]。

图3 ATC-34铰属性定义
本文采用自定义弯矩曲率曲线来定义塑性铰的本构关系,如图4、图5所示。将弯矩(M)塑性铰赋予梁的两端,轴力和弯矩相关(P-M)铰赋予柱两端。均假定出现在距杆端0.05L和0.95L位置(L指扣除刚域后的杆长)。
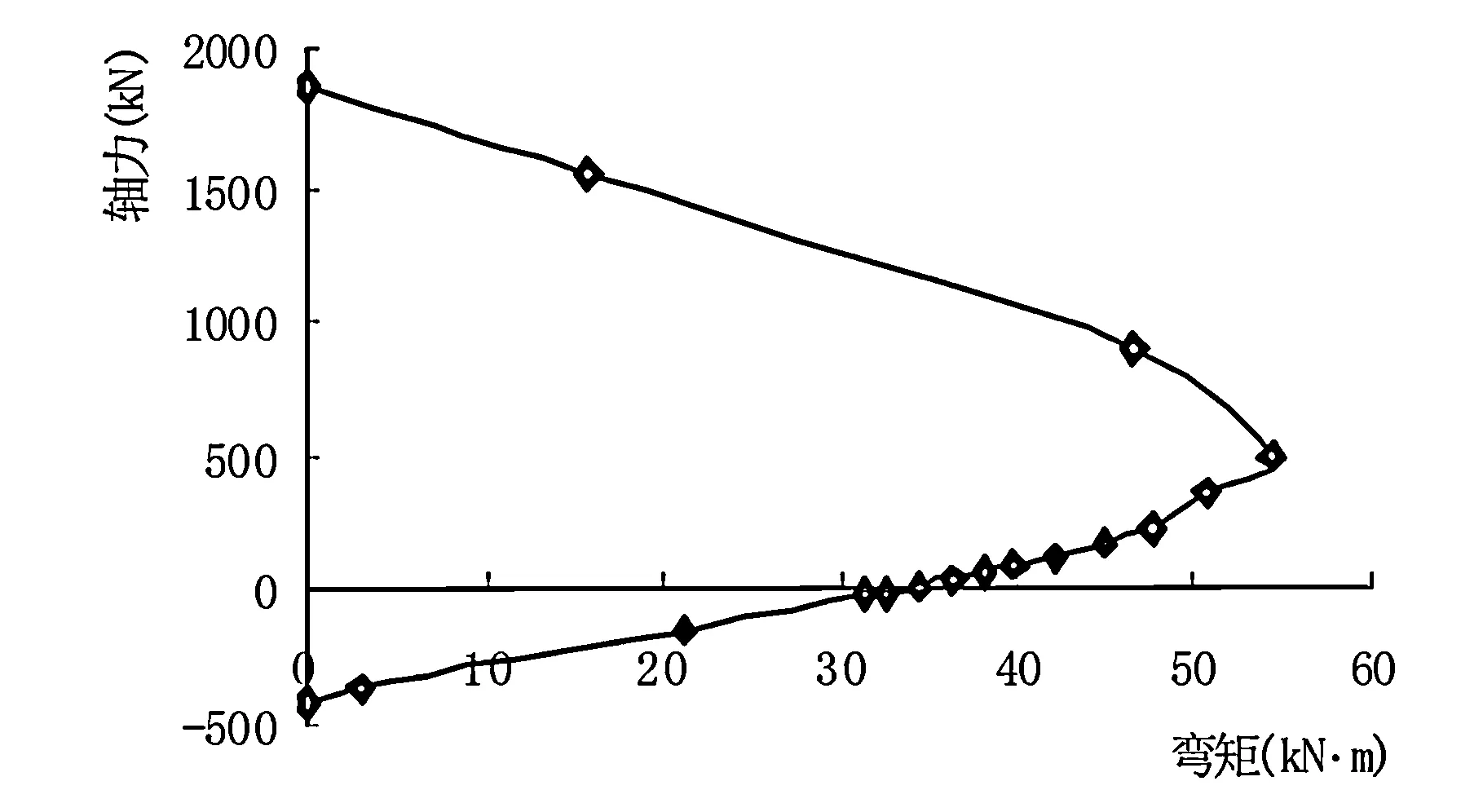
图4 柱P-M屈服面
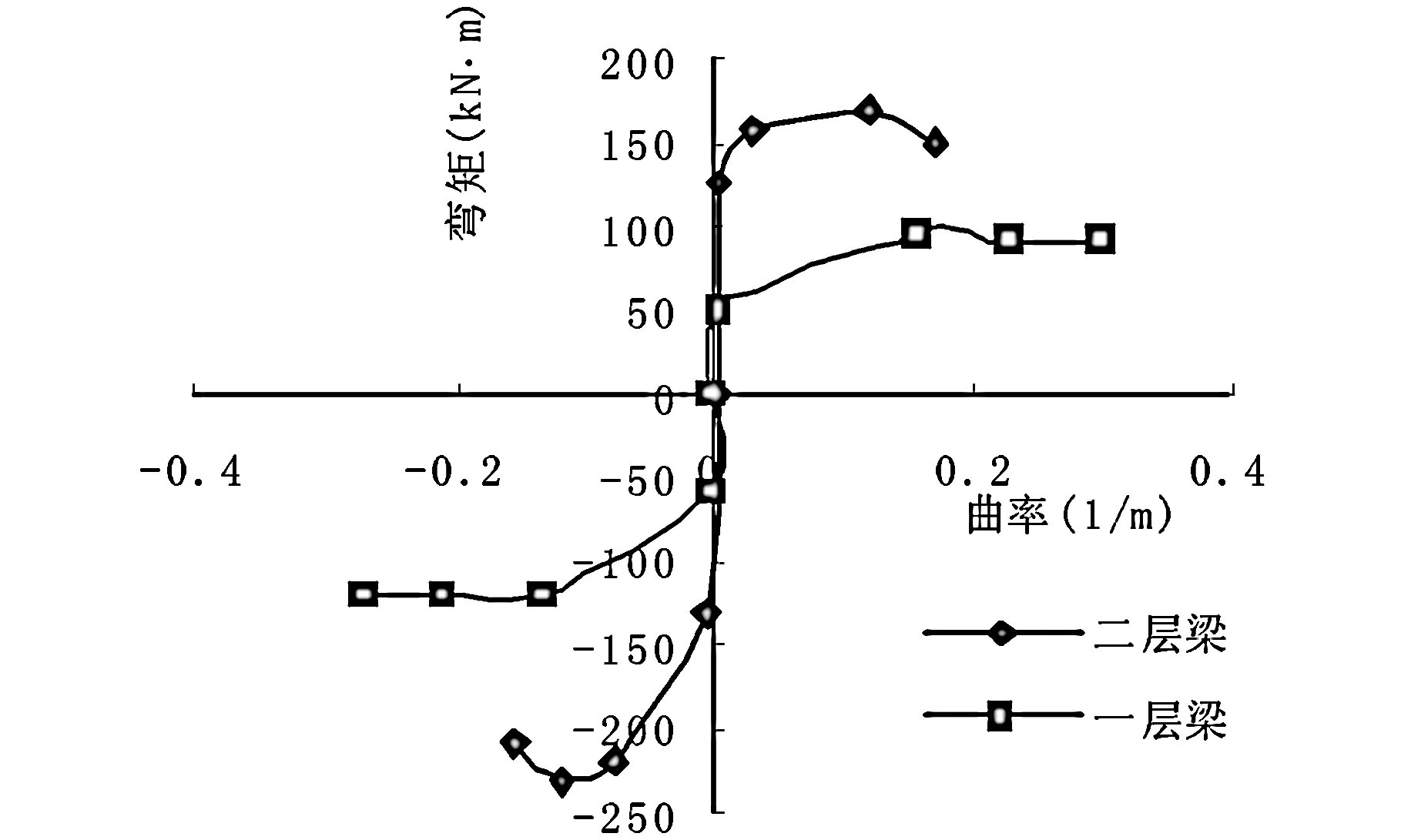
图5 梁弯矩-曲率曲线
2.3 侧向加载方式
本文中采用的是SAP2000程序提供的振型(model)荷载分布,其侧向力是用给定的振型和该振型下的圆频率的平方(ω2)及相应质量分布的乘积获得的,由于采用的是第一振型,故相当于倒三角分布[7]。
2.4 反应谱参数转换
由于程序中采用的是ATC-40中以CA、CV为地震系数的反应谱曲线,与我国《建筑抗震设计规范》(GB50011-2001)的地震反应谱表达方式及系数略有不同,需经等效转换[8]。采用的转换式为:
根据上式可得:
7度多遇地震:CA=0.038,CV=0.036;
7度罕遇地震:CA=0.236,CV=0.225。
3 结构抗震性能分析
基于倒三角分布侧向荷载作用下的结构基底剪力-位移曲线如图6所示。曲线的第一个转折点表明结构中首个塑性铰的出现,而下降点表明首个B性能点的出现,结构丧失承载能力。采用通用屈服弯矩法确定框架模型的延性系数约为4.54,符合规范中对于框架结构延性系数的要求。性能点状态时的结构各层侧移及层间位移(图7)表明,结构变形以剪切变形为主,符合框架结构的变形特点。

图6 基底剪力-位移曲线
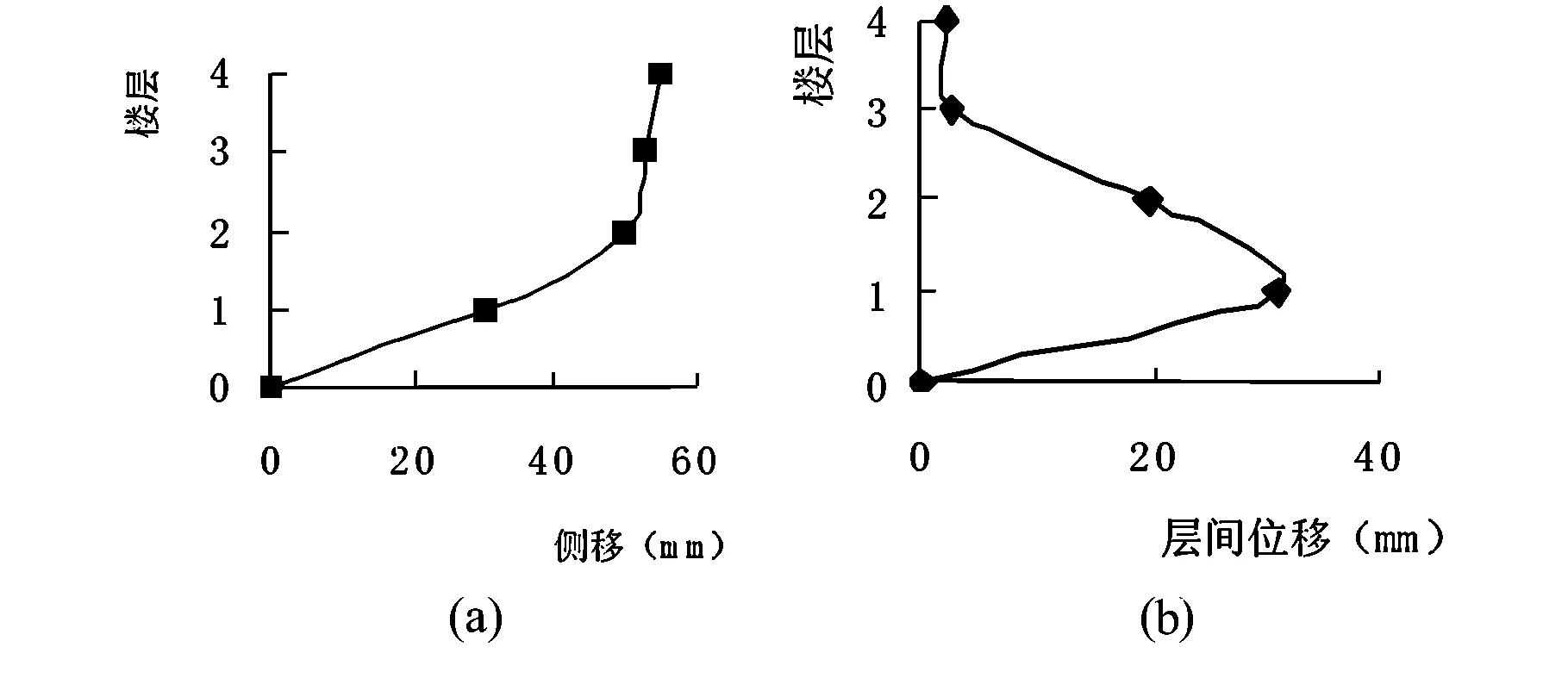
图7 性能点时的各层侧移与层间位移
由计算反应谱可知7度地震作用下的基底剪力与顶点位移,如表1所示。

表1 7度地震作用下性能点及层间位移角
7度多遇地震作用下,结构的顶点位移为1.49 mm,小于能力谱计算中的8.08 mm,表明结构处于弹性阶段,没有构件出铰。
7度罕遇地震作用下,结构的顶点位移为9.18 mm,略大于能力谱计算中的8.08 mm,但仍满足抗震规范中规定的框架结构弹性层间位移角限值为1/550的要求。
结构的能力谱曲线与其需求谱曲线均有交点,且性能点基本位于结构能力谱曲线上的第一阶段,表明结构没有出现塑性铰,整体处于弹性状态。对比7度地震作用下的结构反应,认为该结构能满足7度地震作用下的抗震要求,且符合两阶段设计的结构设计原则。
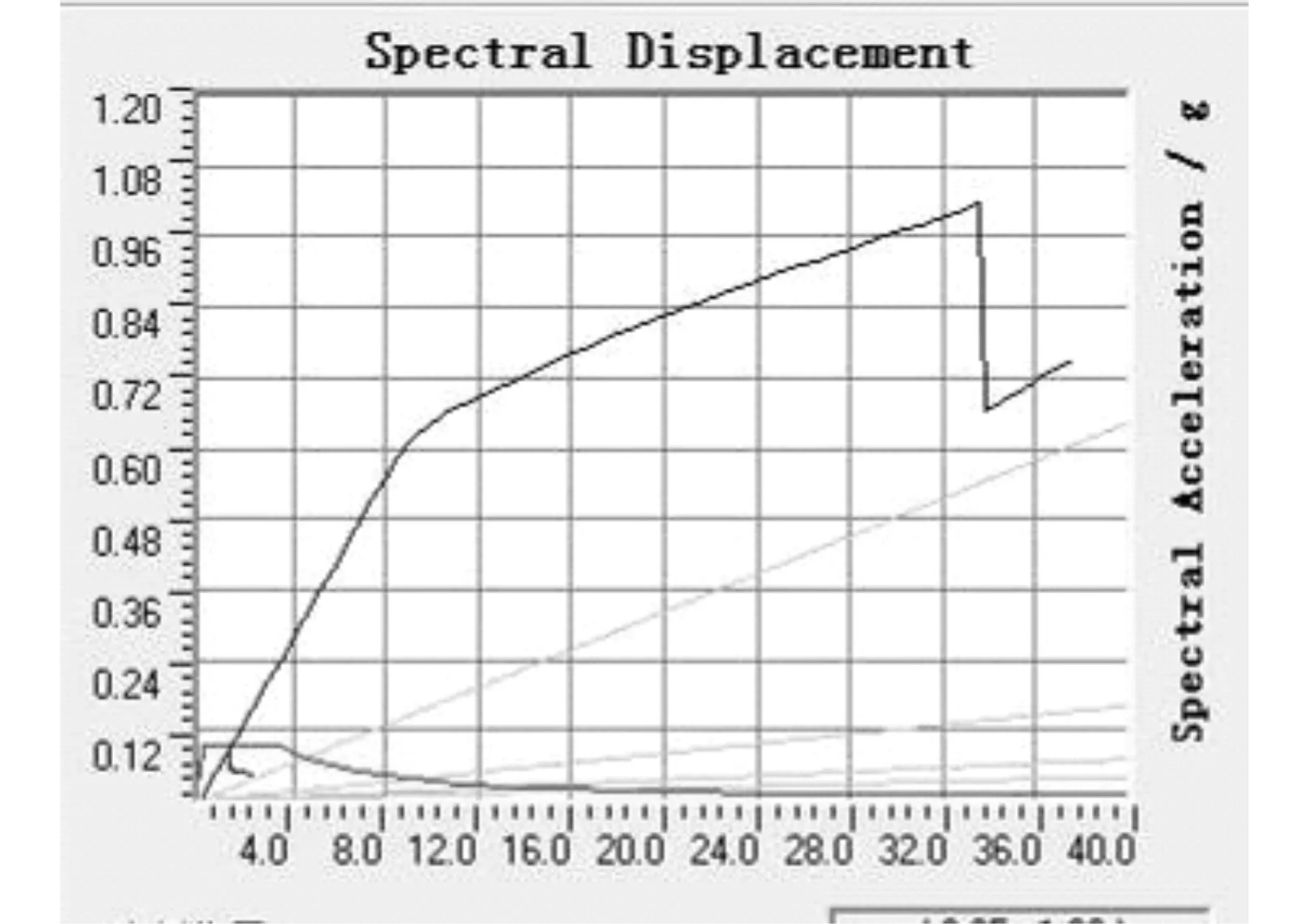
图8 7度多遇地震能力谱与需求谱
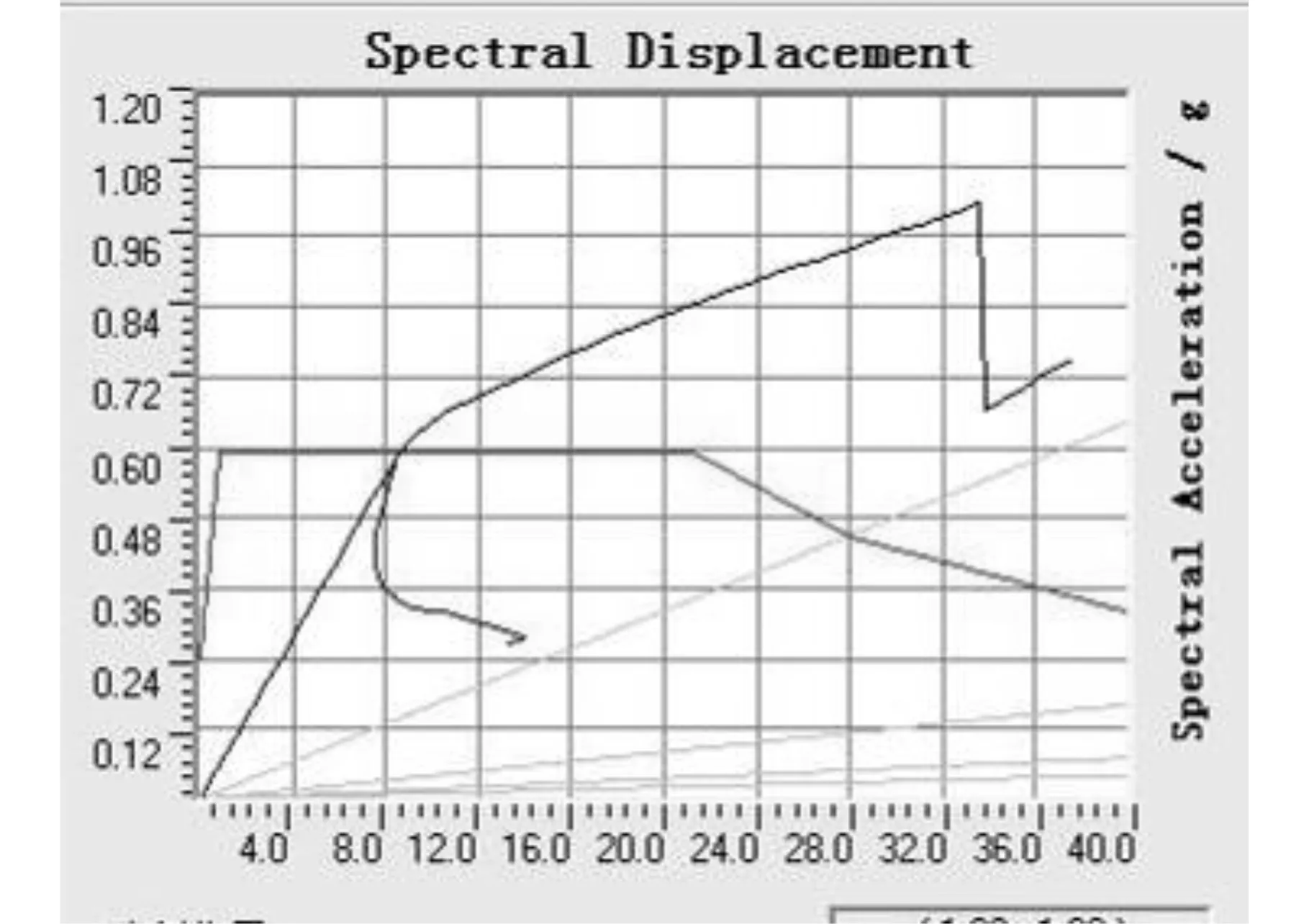
图9 7度罕遇地震能力谱与需求谱
4 静力弹塑性与试验结果对比
对比分析模型与拟静力试验模型的破坏形态表明,最初出铰位置均为柱端,表明结构的薄弱环节为柱底,最终破坏都是因为底层柱失效,符合框架结构在地震作用下的结构反映特点。最终破坏形态,试验模型表现为节点与柱底同时破坏,结构为梁柱混合机制,而SAP模型中为柱端铰丧失承载力,表现为柱铰机制。表明实际工程中,由于节点处受弯剪扭共同作用,受力更复杂,而基于杆系结构的SAP模型无法表现这一特点。
通过对比还发现,结构破坏主要集中在有较大荷载的第一、二两层,表明该结构受竖向荷载影响较大,结构的整体薄弱层为第一、二两层。三、四两层因为竖向荷载较小,地震作用不大,未发生破坏。
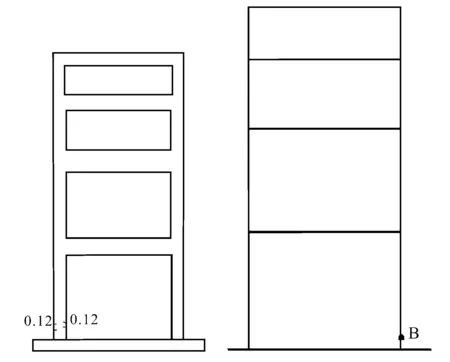
图10 初始出铰位置

图11 最终破坏形态
对比薄弱层的层间剪力-位移曲线表明:
1层P-Δ曲线在弹性阶段拟合较好,但实际模型由于受加工误差和试验中加载误差等各种情况影响,塑性分析阶段分析值的位移小于实测值。
2层P-Δ曲线拟合较好,但分析模型的层间位移仍略大于试验模型。

图12 1层P-Δ曲线
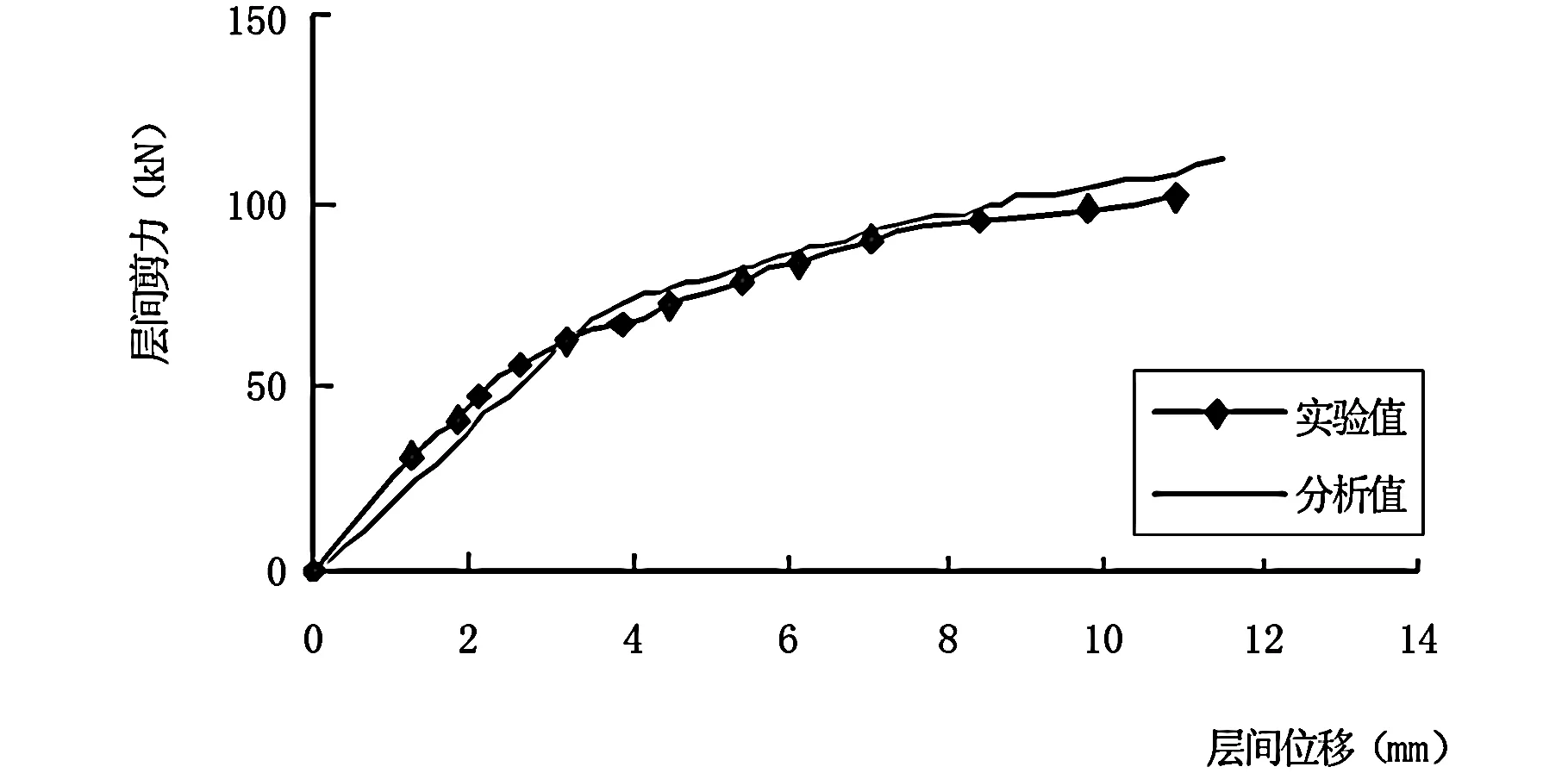
图13 2层P-Δ曲线
5 结 论
(1)拟静力试验与静力弹塑性分析在初始结构的出铰位置、结构破坏形式、结构薄弱环节上一致,表明静力弹塑性分析是一种较为准确的评估结构抗震性能的方法,应加以推广使用。
(2)该结构最先出铰位置在柱底,为梁柱混合出铰机制。底层柱为结构的薄弱环节,在设计上应引起注意,可采用全程箍筋加密或设置核心柱来提高结构的抗侧向荷载的能力。
(3)结构的能力谱曲线表明混凝土结构进入塑性阶段后其承载力变化较小而位移变化较大,应采用基于位移的抗震设计方法加以辅助分析,对于7度以上的高烈度地区的重点抗震设防建筑,如大型火电厂等,应限制混凝土结构的使用。
[1]GB 50011-2001,建筑抗震设计规范 [S].
[2]张 巍,孟少平,吕志涛.预应力混凝土抗震延性的静力弹塑性分析[J].工业建筑,2002,32(6):36-38.
[3]种 迅, 孟少平.钢筋混凝土框架结构全过程pushover分析[J].地震工程与工程振动,2005,25(1):38-42.
[4]俞瑞芳.钢筋混凝土框架结构Pushover-能力谱法分析研究[D].西安:西安理工大学,2002.
[5]田 颖,钱稼茹,刘凤阁.在用Rc框架结构基于位移的抗震性能评估[J].建筑结构,2001,31(7):53-56.
[6]张 巍,孟少平,吕志涛.预应力混凝土框架结构抗震延性的静力弹塑性分析[J].工业建筑,2000,(6):36-38.
[7]李 刚,程耿东.基于性能的结构抗震设计——理论、方法与应用[M]. 北京:科学出版社,2004.
[8]汪梦甫,周锡元.高层建筑结构抗震弹塑性分析方法及抗震性能评估的研究[J].土木工程学报,2003,36(11):44-49.

