“牛顿水桶”液面方程的几种巧解

孙伏优

(南京师范大学附属中学江宁分校 江苏 南京 211102)

牛顿在1689年构思了一个理想实验，即著名的“水桶实验”．在“水桶实验”中，一个注水的水桶起初保持静止．当它开始发生转动时，水桶中的水最初仍保持静止，但随后也会随着水桶一起转动，于是可以看到水渐渐地脱离其中心而沿桶壁上升形成凹状，直到最后和水桶的转速一致，水面相对静止．辩证力学的理论预言是：在地球的引力场内，旋转水桶中水面形状由平变凹，其形状是抛物线旋转曲面．笔者尝试从几种不同角度证明最后稳定时液面的形状是抛物线旋转曲面．

建模：牛顿水桶实验可视为切线力等于零的平衡运动，所以，牛顿水桶可以当做刚体．现任取曲面的一个截面，试证明其为抛物线．

图1

方法一：从曲线上取一点水P，受法向力N和重力mg，P点的切线与x轴夹角为θ，不难证明N与mg的夹角为(π-θ)，由于水滴P做匀速圆周运动，所以合力指向圆心提供水滴P做圆周运动的向心力，如图1所示.由平行四边形法则可得N与mg的合力F合．

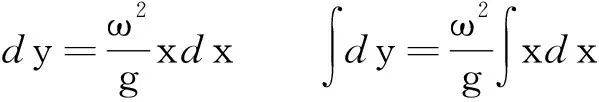
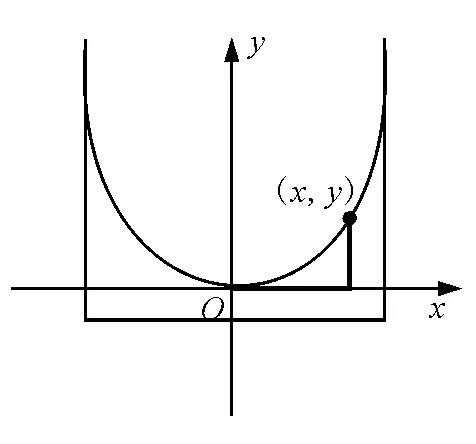
图2

方法二：从液面上任取一点(x,y)，构建如图2所示的水平小液柱x和竖直小液柱y，那么水平小液柱x做圆周运动的向心力来源于竖直小液柱y的压力．设液体密度为ρ，小液柱截面为ΔS，得

同理可得液面方程

说明：不难证明均匀棒绕其一端做圆周运动时，可将其等效为质量集中在中点的质点做圆周运动．

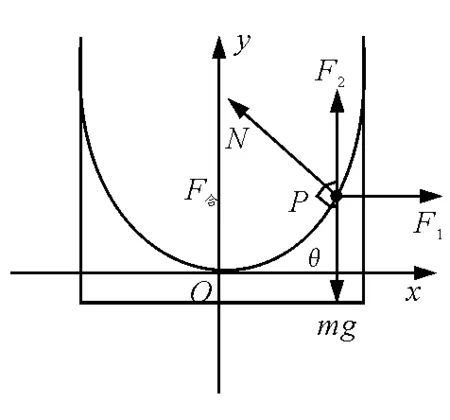
图3

方法三：从曲线上取一点水P，坐标为(x,y)，其受重力mg、法向力N、水平向外惯性力F1=mω2x、竖直向上惯性力F2=mg，如图3所示．则x方向合力为零，y方向合力沿y正方向大小为mg，那么水滴的运动可视为平抛运动．则

x=v0t

(1)

(2)

由(1)、(2)式得

在P处的速度方向为该点切线方向，而F1与重力mg的合力与N等大反向，则

同理可得液面方程