用整体法求解漂浮型问题*

邵建新 张子英 曹海宾 刘云虎 林春艳 唐光辉

(石河子大学师范学院 新疆 石河子 832003)

浮力是流体静力学中应用性较强的基础知识之一，也是在力、二力的合成、二力平衡、同一直线上力的合成及平衡、密度和液体内部压强等知识的综合学习内容，因而成为教学和考试的重点；由于其综合性，又使其成为教学的难点．浮力中有关“漂浮型”问题求解，则是难中之难，不少教师对此提出过一些求解方法，但我们觉得都过于繁难不便学生掌握．经过仔细研究，我们发现，常见的“漂浮型”问题，可用“整体法”统一求解．下面我们以常见问题求解为例说明之．

1 一些典型问题的分析

问题1：如图1(a),装有铁块的烧杯漂浮在小水池水面上，若将烧杯中的铁块取出并投入小水池中，如图1(b).问小水池水面的高度如何变化？

图1

解析: 若将铁块和烧杯分别进行研究，求解繁难.一方面，铁块投入小水池中后，占据一定体积，使水面上升；另一方面，由于烧杯中铁块的取出，烧杯的排水量减少，使水面下降 ．要综合分析两种因素谁占上风，实属不易．但如果铁块投入小水池前后，始终把烧杯和铁块当作一个整体作为研究对象，则问题会明了得多．设烧杯和铁块的重量分别G杯、G铁，铁块投入小水池前后，烧杯和铁块这个整体排开水的体积分别为V前、V后，要知道水面是否变化，只要比较V前、V后的大小即可．

下面分析铁块投入小水池前后研究对象的受力情况及其运动状态．

铁块投入小水池前，研究对象的受力情况为，竖直向下的重力G杯、G铁，竖直向上的浮力ρ水gV前；研究对象的运动状态为静止(平衡态)．故知研究对象受到的竖直向下的力等于竖直向上的力，即

G杯+G铁=ρ水gV前

(1)

铁块投入小水池后，研究对象的受力情况为，竖直向下的重力G杯、G铁，竖直向上的浮力ρ水gV后及池底对铁块的支持力N；研究对象的运动状态为静止(平衡态)．故知研究对象受到的竖直向下的力等于竖直向上的力，即

G杯+G铁=ρ水gV后+N

(2)

因N≠0

(3)

由(1)、(2)、(3)式可知

ρ水gV后<ρ水gV前

即

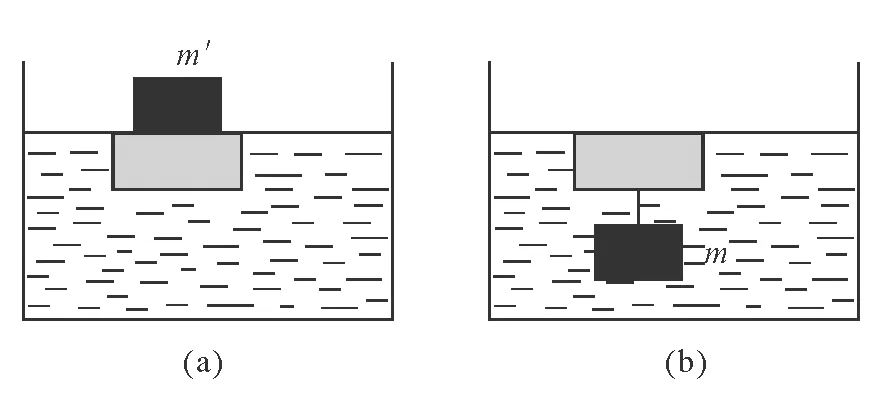
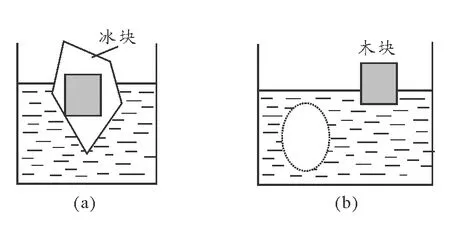
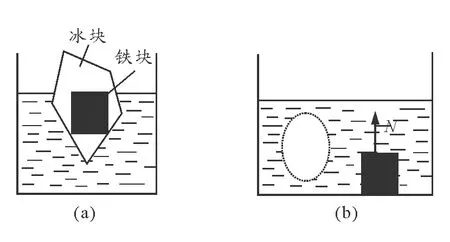
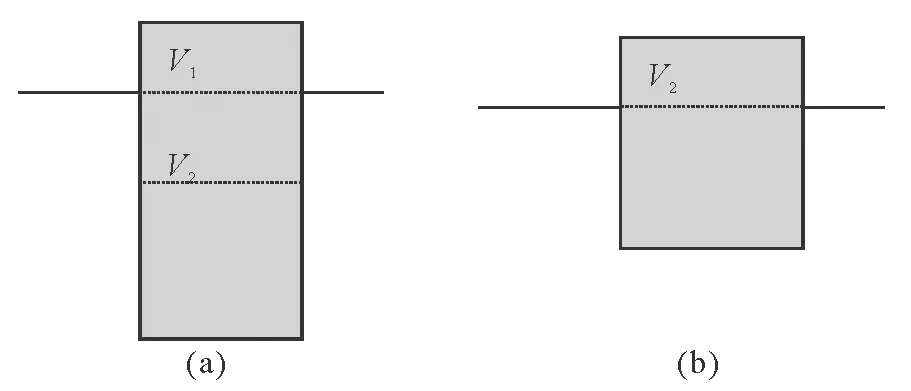
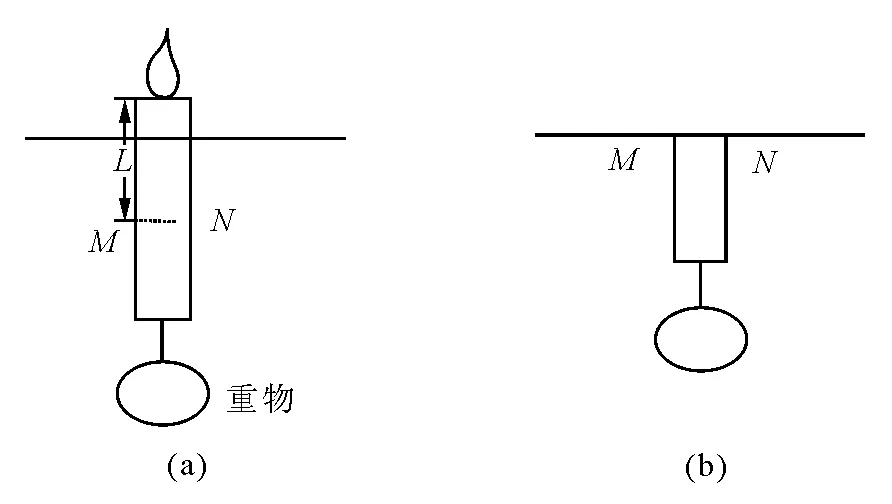
V后

即池中水面下降.

由以上解析可以看出,求解这个问题的关键在于将烧杯和铁块作为一个整体,分析两者分离前后整体的受力情况,然后根据这个整体分离前后均处于平衡态得到两个平衡方程,最后再根据所给其他条件使问题得到解决．

问题2：漂浮在小水池中的小船下，悬吊着重物P．若把悬吊重物的绳子剪断，重物P将沉入水底，这时水面将________；若把重物从水中拉上来，放到船舱内，这时的水面与重物吊在船下时的水面相比将________(填“上升”、“下降”、“不变”)．

图2

解析: 三种情况如图2(a)、(b)、(c)所示．选船和重物P这个整体作为研究对象．设图(a)、(b)、(c)三种情况下船和重物P排开水的体积分别为Va、Vb、Vc，船的重量为G1，重物的重量为G2.

对图2(a)状态有

G1+G2=ρ水gVa

(4)

对图2(b)状态有

G1+G2=ρ水gVb+N

(5)

N≠0

(6)

对图2(c)状态有

G1+G2=ρ水gVc

(7)

由(4)、(5)、(6)式可得

ρ水gVb<ρ水gVa

所以

Vb

即池中水面下降.

由(4)、(7)式可得

ρ水gVa=ρ水gVc

故

Vc=Va

即池中水面不变．

问题3：如图3(a)所示，把质量为m′的铁块放在木块上面，刚好把木块淹没在水中.如果把质量为m的铁块系在木块下面，也刚好把木块淹没在水中，如图3(b)所示.求m′与m的比值．

图3

解析: 将木块和铁块看成整体作为研究对象．设木块的体积为V．

对图3(a)有

m′g+ρ木gV=ρ水gV

(8)

对图3(b)有

mg+ρ木gV=ρ水gV+ρ水gVm

(9)

式中Vm为铁块m的体积.

(10)

由(8)、(9)、(10)式可得

问题4：如图4(a)所示,盛有水的容器中,水面上浮着一块冰．当冰完全融化后，容器中的水面是否变化？怎样变化？

解析: 这也是一道很流行的题目．通常的解法是先选冰为研究对象，根据它是漂浮状态及阿基米德原理求出冰块排开水的体积V2,再求出冰块完全融化后所占的体积V2＇，如图4(b).由此比较可得出

V2＇=V2，即水面位置不变，但推理过程较复杂．若用整体法求解，设冰块在水中的体积为V2,露出水面的体积为V1，冰块及冰块融化为水后的重量分别为G冰、G水．选整个冰块为研究对象.对图4(a)有

图4

G冰=ρ水gV2

(11)

选冰块融化成的水为研究对象.对图4(b)有

G水=ρ水gV2＇

(12)

注意到冰块融化为水后,重量不变，故有

G冰=G水

(13)

由(11)、(12)、(13)式 可得

V2＇=V2

即水面位置不变.

问题5：在问题4中，若冰块中有一木块，如图5(a)所示.当冰块完全融化为水后，容器中的水面是否变化？怎样变化？

解析：将冰块和木块看成一整体作为研究对象．设冰块融化前整体排开水的体积为Va,冰块完全融化为水后整体排开水的体积为Vb，(包括冰块完全融化为水后的体积和木块排开水的体积之和),如图5(b)所示.

图5

对图5(a)有

G冰+G木=ρ水gVa

(14)

对图5(b)有

G水+G木=ρ水gVb

(15)

注意到冰块融化为水后,重量不变，故有

G冰=G水

(16)

由(14)、(15)、(16)式可得

Vb=Va

即水面位置不变.

问题6：在问题4中，若冰块中有一铁块，如图6(a)所示.当冰块完全融化为水后，容器中的水面是否变化？怎样变化？

解析: 将冰块和铁块看成一整体作为研究对象．设冰块融化前整体排开水的体积为Va；冰块完全融化为水后整体排开水的体积为Vb(包括冰块完全融化为水后的体积和铁块排开水的体积之和),如图6(b)所示.

图6

对图6(a)有

G冰+G铁=ρ水gVa

(17)

对图6(b)有

G水+G铁=ρ水gVb+N

(18)

注意到冰块融化为水后,重量不变，有

G冰=G水

(19)

又容器底部对铁块的支持力不为零，即

N≠0

(20)

由(17)、(18)、(19)、(20) 式可得

Vb

可知水面位置下降．

请思考，问题5和问题6的结论与木块或铁块在冰块中的位置有无关系？

以上例题涉及到的均是整体的重力不发生变化的情形.若整体的重力发生变化，仍可用整体法求解．

问题7：一木块浮在水面上，露出水面的体积是V1；把它露出水面的部分截去，原水下部分又有体积V2露出水面．求这块木块的密度．

图7

解析: 选木块整体作为研究对象．依题意作出 图7(a)、图7(b) ，因在两状态时木块均处于平衡态，故有

Fa浮=Ga物

(21)

Fb浮=Gb物

(22)

两式相减，得

Fa浮-Fb浮=Ga物-Gb物

(23)

上式的物理意义是，从图(a)态到图(b)态的变化过程中，木块所受浮力的减少等于其重量的减少．由此可得

ρ水gV2=ρ木gV1

即

问题8：有一粗细均匀的蜡烛下端挂一重物后，放入水中漂浮在液面上，有1 cm露出水面．将蜡烛点燃，让它一直烧至淹灭.求燃烧掉的那部分蜡烛的长度为多少？(ρ蜡=0．9×103kg/m3)

解析: 设 燃烧掉的那部分蜡烛的长度为L，在L处画一截面MN，选蜡烛及下端挂的重物为一整体作为研究对象．依题意作出 图8(a)、图8(b) ，因在两状态时研究对象均处于平衡态，故有

Fa浮=Ga物

(24)

Fb浮=Gb物

(25)

两式相减，得

Fa浮-Fb浮=Ga物-Gb物

(26)

上式的物理意义是，从图(a)态到图(b)态的变化过程中，研究对象所受浮力的减少等于其重量的减少．由此可得

ρ水g(L-1)S=ρ蜡gLS

式中S为蜡烛的横截面积.算得

L=10 cm

图8

2 方法总结

由以上数例可以看出，用整体法求解的基本思想是,选择一个合适的整体作为研究对象.在具体分析整体受力时,可以不考虑整体内部物体间的相互作用，只需考虑外界物体对整体的作用力；然后利用整体在状态变化前后均处于平衡态可得到相关方程；最后结合所给其他条件可使问题得到解决．