归类例析圆形边界磁场中的圆弧运动

徐正恒

(衡阳县第一中学 湖南 衡阳 421200)

带电粒子在圆形边界磁场中运动是历年来高考的一个重点和热点，题型多，装置复杂，解答方法也很多，突出考查学生分析综合能力和应用数学知识处理物理问题的能力．下面就该问题进行归类分析，探究这一问题快捷、有效的解答方法．

1 内圆形边界

1．1 正对圆心从圆形边界外射入磁场

带电粒子在磁场中运动速度v越大→轨道半径R越大→圆心角α及偏向角β越小，所以粒子在磁场中运动的时间t越小．

求带电粒子在磁场中运动的时间t的方法是连接两圆圆心O2O(图1)，求出圆心角α.设磁场圆半径为r，轨迹圆半径为R，则

所以

又

所以

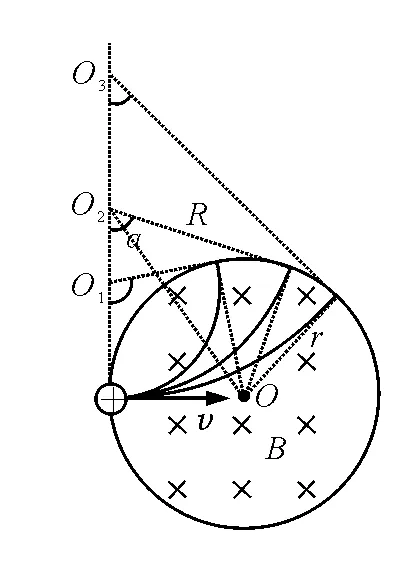
图1

【例1】如图2所示，在半径为R的圆形区域内，有磁感应强度为B、方向垂直纸面向里的匀强磁场；a、b、c三点均匀分布在圆周上，三对电压为U、间距为d的平行金属板通过三点与圆相切，并有小孔通向磁场．一个质量为m、电荷量为+q的粒子，从S点由静止开始运动，经过一段时间恰好又回到S点，试问：

(1)电压U与磁感应强度B应满足什么关系？

(2)粒子从S出发到第一次返回S需多长时间？

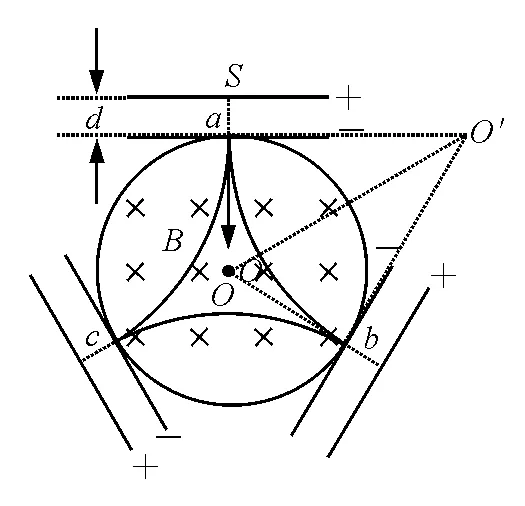
图2

所以

粒子在电场中运动时间为

所以运动总时间为

1.2 从圆形边界外任一点射入磁场

【例2】如图3所示，半径R=10 cm的圆形匀强磁场区域边界跟y轴相切于坐标系原点O，磁感应强度B=0.332 T，方向垂直于纸面向里，在O处有一放射源，可沿纸面向各个方向射出速率均为v=3.2×106m/s的α粒子，已知α粒子的质量m=6.64×10-27kg，电荷量q=3.2×10-19C．

(1)画出α粒子通过磁场空间做圆周运动的圆心点轨迹，并说明作图的依据；

(2)求出α粒子通过磁场空间的最大偏转角；

(3)再以过O点并垂直于纸面的直线为轴旋转磁场区域，能使穿过磁场区且偏转角最大的α粒子射到正方向的y轴上，则圆形磁场区的直径OA至少应转过多大角度？

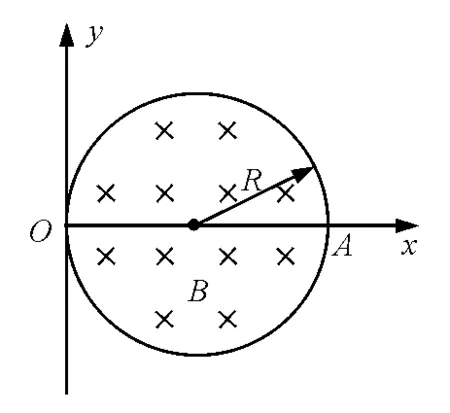
图3

图4

(2)α粒子在磁场中做圆弧运动中的轨迹半径为r大小一定，欲穿过磁场时偏转角最大，须圆弧轨道所夹的弦最大，即OO′A共线，如图5所示．

图5

⑶欲使穿过磁场且偏转角最大的α粒子能射到y轴正方向上，必须使从A点射出的 粒子和x轴正方向的夹角大于90°，根据几何关系可知圆形磁场至少转过60°．

1.3 对圆心射入并与圆形边界多次碰撞反弹

【例3】在半径为r的圆筒中，有沿筒的轴线方向的匀强磁场，磁感应强度为B．一个质量为m，带电荷量为+q的粒子以速度v从筒壁A处沿半径方向垂直于磁场射入筒中，如图6(a)所示，若它在筒中只受洛伦兹力作用且与筒壁发生弹性碰撞，欲使粒子与筒壁连续相碰撞绕筒壁一周仍从A处射出，则B必须满足什么条件？

图6

解析：设粒子从A处射入经与筒壁n次碰撞后，又从A处射出(含返回A处将射出时与A的碰撞)，由图6(b)知粒子在磁场中轨道半径R与圆筒半径r的关系是

R=r·tanα

而图6(b)表示的是n=2时的情况．当n>2时，同样分析可得到关于B的相同的表达式，所以

2 圆环形边界

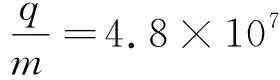
(1)若氦核沿磁场区域的半径方向、平行于截面从A点射入磁场，画出氦核在磁场中运动而不穿出外边界的最大圆轨道示意图，并求出其轨道半径和最大速度．

(2)若氦核平行于截面从A点沿各个方向射入磁场都不能穿出磁场外边界，求氦核的最大速度．

(3)若氦核平行于截面从A点沿各个方向射入磁场，不能穿出磁场外边界的氦核的最大速度为多少？

图7 图8

解析：(1)根据几何知识可得，所求轨迹是圆周的一部分，且当与外圆相切时最大，如图8中曲线Ⅰ所示．

由图中几何关系可得

又由

得

(2)根据题意分析.当氦核以vm的速度沿与内圆相切的方向射入磁场且轨道与同一侧外圆相切时，则以vm速度沿各方向射入磁场区的氦核都不能穿出磁场外边界，如图8中曲线Ⅱ所示．由图中几何关系知

再由洛伦兹力提供向心力得

故

氦核不穿出磁场外边界应满足的条件是

代入数据可求出

(3)根据题意分析.当氦核以vm的速度沿与内圆相切的方向射入磁场且轨道与另一侧外圆相切时，是不能穿出磁场外边界的氦核的最大速度，如图8中曲线Ⅲ所示．由图中几何关系知

再由洛伦兹力提供向心力得

故

氦核不穿出磁场外边界的最大速度应满足的条件是

代入数据可求出

3 圆弧组合型边界

【例5】在xOy平面内有许多电子(质量为m，电荷量为e)，从坐标原点O不断地以相同的速率v0沿不同方向射入第一象限，如图9所示．现加一个垂直于xOy平面向里、磁感应强度为B的匀强磁场，要求这些电子穿过磁场区域后都能平行于x轴向x轴正方向运动．求符合该条件磁场的最小面积．

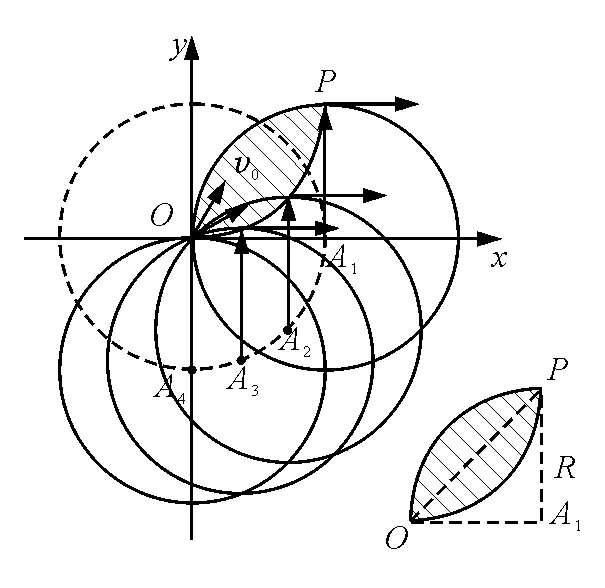
图9

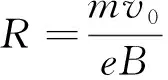
以上通过例题归类分析了带电粒子在各种圆形边界磁场中的部分圆弧运动，从中可以看出定圆心、画轨迹、求半径是解答的关键,巧妙地运用运动特点和几何关系准确地分析临界状态、灵活地运用物理规律是简捷解答的重要方法，按照这样步骤和方法，再难的问题也就能迎刃而解了．