X射线衍射峰基本要素及其在相分析中的应用
张 勇,沈慧娟
(通化师范学院 物理系,吉林 通化 134002)
自从1896年德国著名物理学家伦琴首次拍摄到射线照片以来,射线成像技术得到了迅速的发展,并且在临床医学、生物学、材料科学、信息科学等应用领域得到了非常广泛的应用.从简单物质系统到复杂的生物大分子,射线已经为我们提供了很多关于物质静态结构的信息.在各种测量方法中,射线衍射方法具有不损伤样品、无污染、快捷、测量精度高、能得到有关晶体结构的大量信息等优点.
目前,由于晶体在计算机、航空航天、能源、生物工程等工业领域的广泛应用,人们对晶体的研究日益深入.X射线衍射分析已经成为研究晶体最方便、最重要的手段.
Wang和Zhou[1,2]根据衍射峰的几何特征提出X射线衍射峰是由衍射峰位置(P)、衍射峰形态(Sc)、半高宽(HW)、最大衍射强度(Imax)及对称性(As)五个基本要素(参数)确定(图1).积分宽度和积分强度为两个额外的参数,可由基本参数导出.本文对已建立如图1所示几何关系的各衍射峰参数的物理学意义进行了讨论.
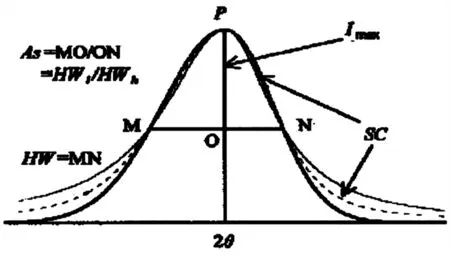
图1 X射线衍射峰的五构成要素
(细实线为Cauchy曲线,粗实线为Gauss曲线,介于其间的细虚线代表曲线的形态变化区)
1 X射线衍射峰五个基本参数及其物理学意义
1.1 衍射峰位置(P)
根据Bragg方程,衍射峰的位置(衍射角θ)是衍射面网间距的函数.因而,衍射峰位置的变化反映所对应的衍射面网间距的变化.关于衍射峰位置的确定有如下几种方法:①直接法,直接由最大(最高)计数点所对应的衍射角度确定;②平滑最大值法,即数据平滑后由具有一阶导数为零且二阶导数小于零的点对应的衍射角度确定;③拟合法,利用函数曲线拟合测量曲线,用最好拟合程度的函数曲线确定衍射峰位置.因此,衍射峰的位置实际上反映面网间距的大小.
1.2 衍射峰半高宽(HW)
Scherrer[3]提出的衍射峰半高宽与Bragg衍射角及对应衍射面网总厚度(通常可作为粒度大小)的关系式Dc=0.89λ/(HWcosθ)(Dc为粒度的大小,λ为X射线波长,HW为衍射峰半高宽,θ为衍射角),总体上反映了衍射峰变宽与厚度变薄(小)的规律.对于某个衍射峰,尤其是能够反映晶体某方向厚度的衍射峰,如层状硅酸盐(00l)衍射峰,应用Scherrer关系式就可方便地计算出样品颗粒的平均厚度,或者平均体积、平均面积厚度.Scherrer关系式中常数K的选取是有一定原则的,并不总是0.89或0.90或1.00.常数K的选取取决于晶体的形态和晶面指数hkl,换句话说,常数K实际上是晶体形态和面网指数的函数.Wilson[4]计算了球体、四面体、八面体、立方体和具有三边不同长度的直角平行六面体不同晶面hkl面网的常数K取值,使我们有了较多的选择,可以较高精度地计算许多晶体的三维长度(或厚度).当然,其它晶体的粒度计算亦可用K=1来近似完成.衍射峰半高宽可近似反映样品粒度大小,某些特定衍射峰半高宽可作为某些结晶度的基础.
1.3 衍射峰形态(Sc)
衍射峰的形态是一个并不太引起人们注意的参数.它所反映的物理学意义鲜为人知.我们定义衍射峰的形态参数对于对称衍射峰是一个描述除了衍射峰位置、衍射峰高度和衍射峰宽度变化以外的其它变化的参数.这些变化主要表现在衍射峰顶部的宽缓尖锐程度上的差异,而造成这种差异的原因就是反映衍射峰形态的物理学意义.从上世纪60年代至今,不少学者从理论和实验上验证了以下假设的成立,即衍射峰形态的Cauchy分布是唯一由晶畴大小引起的,而衍射峰形态的Gauss分布则由晶体内部的晶格错位或应变产生的.由此可见,衍射峰形态特点反映了晶畴大小与应变大小对衍射贡献程度上的不同.衍射峰形态特点的描述可由衍射峰形态系数(shape coefficient)表示.因而,衍射峰形态特点是粒度与应变对衍射作用贡献大小的度量.即衍射峰形态是粒度与应变衍射效应的函数.
1.4 最大衍射强度(Imax)
最大衍射强度是指衍射峰的最大高度,正常情况下与衍射峰Bragg衍射角位置所对应的峰具有的强度一致.从几何关系上衍射峰的总强度(II,即衍射峰面积或衍射峰积分强度)与半高宽和衍射峰形态系数具有如下关系[1,2]:
II=HWImax/Sc
(1)
且衍射峰总强度与仪器因素、光学因素及结晶学参数有如下的关系:
II=I0kWfAT(1/V2)(1/ρ)|F|2(1+cos22θ)(1/sin2θ)ψ(1/μ*)
(2)
HWImax/Sc=I0kWfAT(1/V2)(1/ρ)|F|2
(1+cos22θ)(1/sin2θ)ψ(1/μ*)
(3)
Imax=I0kWfAT(1/V2)(1/ρ)|F|2(1+cos22θ)
(1/sin2θ)ψ(1/μ*)Sc/HW
(4)
式中I0为入射X射线强度,Wf为样品中所研究物相的重量百分数,A为重叠因子,T为温度因子,V为单位晶胞体积,θ为所研究物相密度,|F|为Bragg衍射方向上原子散射振幅的模数,也称结构因子,(1+cos22θ)为极化因子,(1/sin2θ)为单个晶体Lorentz因子,ψ为样品环状分布因子,μ*为样品平均质量吸收系数.k为物理学常数,等于许多物理学常量的乘积,如电子的质量和电荷量、光速、入射X射线波长,并受探测器的效率、单色器或β射线滤波器具有的透射特征和狭缝系统等的影响.由于(4)式中,Sc/HW=1/IW,1/IW为积分宽度的倒数.由此可见,最大衍射强度是消除了宽化效应的衍射峰总强度.它是极为重要的晶体结构信息、物相衍射特征(对X射线的吸收作用)、衍射仪系统几何特征、衍射环境特征和衍射角度特征的总和.
1.5 衍射峰的对称性(或不对称性)(As)
聚合物的X射线衍射(峰)在低角度区(2θ<15°)通常易产生不对称现象.按照几何特点不对称衍射峰可分为左右直线[3]、左右宽度、左右形态、左右宽度和形态、上下和综合不对称等6种[4].关于造成衍射峰不对称现象的原因目前有多种解释:如仪器的偏差;样品的透明度或吸收因子的作用[3];样品的几何特征[2];原子散射因子[3]及其它物相衍射存在的影响[3].通常,前4种原因都可产生左右不对称现象.其中测角仪精度在相对衍射峰宽度较大时或衍射峰形态系数(SS/HW)[4]较大时可产生上下不对称衍射峰(图2).
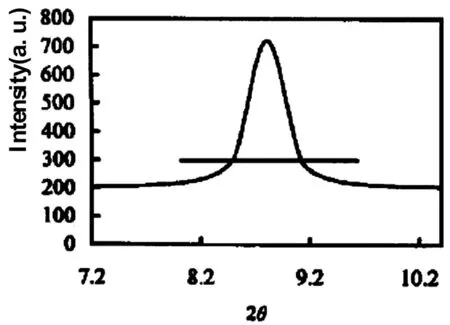
图2 衍射峰的上下不对称
(水平线之上为Gauss分布,之下为Cauchy分布,构成上下形态不对称)
描述衍射峰的不对称可按照其类型分别使用不同的指数(As)进行.如对于左右宽度不对称:
ASHW=HWh/HW1
其中HWh和HW1分别为衍射峰高角度一侧半高宽和低角度一侧半高宽(见图1中As).左右形态不对称:AsSc=Sch/Scl.其中Sch和Scl分别为衍射峰高角度一侧形态系数和低角度一侧形态系数.
左右宽度和形态不对称:
AsHW-Sc=HWhSch/HW1Sc1
Asupper-lower-HW=HWupper/HWlower
上下不对称:
Asupper-lower-Sc=Scupper/Sclower
其中下标upper和lower分别表示衍射峰(某高度)较上部分和较下部分.当衍射仪狭缝系统固定不变,而测角仪由低向高扫描时,由于照射面积的不同,因而在不同的衍射角度会产生不同的衍射强度,且低角度照射面积大,高角度照射面积小,因此同一衍射峰在低角度一侧衍射强度强而在高角度一侧衍射强度弱,这样就构成了衍射峰的不对称.又由于在低角度区这种变化强而在中高角度区这种变化弱,所以,衍射峰的不对称现象只出现在低角度区,在中高角度区通常观测不到不对称现象.
1.6 衍射总强度和积分宽度(II与IW)
根据五个要素的基本几何关系,衍射总强度即衍射峰的面积等于最大衍射强度与半高宽之积除衍射峰形态系数[1],故:II=HW×Imax×Sc-1
积分宽度等于衍射峰面积除最大衍射强度,即衍射峰等面积矩形宽度(图3),故:
IW=II/Imax=HW×Sc-1
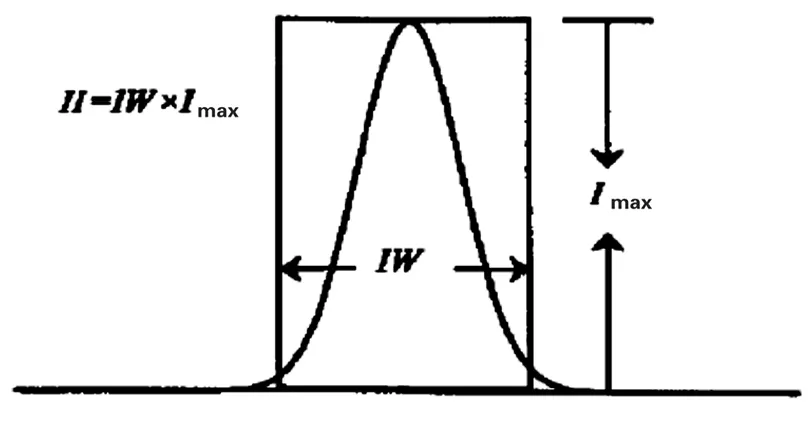
图3 积分强度(II)和积分宽度(IW)的图示
2 应用
2.1 衍射峰形态变化与粒度大小测量
根据Scherrer方程,由积分宽度可测定粘土矿物的层堆积厚度,即粘土矿物的粒度大小.样品HW-297中伊利石的(001)衍射峰积分宽度为0.801°,Δ2θ,CuKα,由此可计算出伊利石的粒度为10nm(图4).
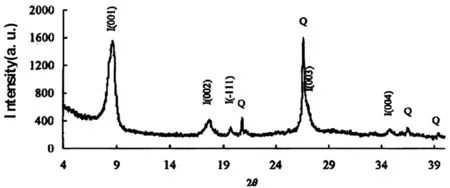
图4 样品HW-297[10nm级伊利石(I)与石英(Q)共存]的衍射图
2.2 衍射峰形态变化与应变大小测量
由KI-Wv定量图解[4]不仅可确定层状硅酸盐粒度大小而且还可方便得出粘土矿物c轴方向上(即垂直片理方向)应变量大小.如根据绿泥石0.7nm衍射峰半高宽和特定强度比,得出样品HW-229中绿泥石c轴方向应变量为0.0069nm或1%(图5,其粒度为44nm).
2.3 衍射强度变化与物相百分含量分析
根据Alexander关系式,某物相的某衍射峰的衍射强度与物相在样品中的百分含量成正比,故衍射峰的积分强度直接反映了物相在化合物中的百分含量.积分强度即衍射峰面积与最大衍射强度、半高宽成正比,而具有Cauchy分布的衍射峰在面积上是具有Gauss分布的衍射峰面积的1.48倍.这主要是Cauchy曲线的下部比Gauss曲线宽造成的(图1).
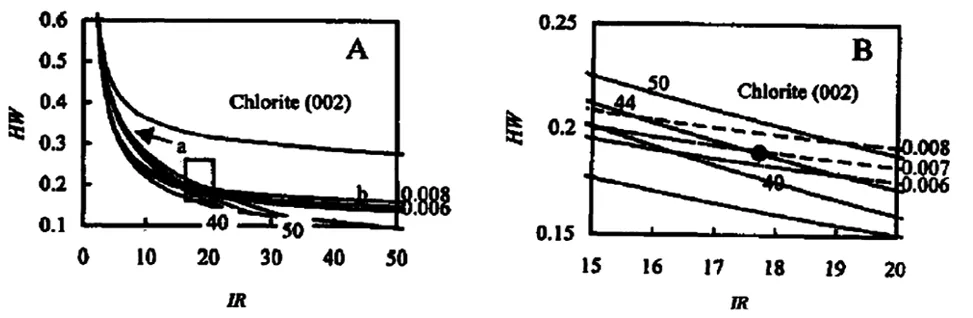
图5 样品HW-229绿泥石c轴方向的粒度大小和应变大小(nm)的HW-IR图解
A.一般HW-IR图解(a为等粒度曲线束,b为等应变曲线束) B.表示A中框出部分的放大
3 结语
单个X射线衍射峰是由相互独立的、各自具有一定物理学意义的五个基本要素组成.衍射峰位置是Bragg衍射角的图形表示,衍射峰的宽度是Scherrer粒度大小的反映,衍射峰的形态是粒度大小和晶格位错的综合反映,衍射峰的强度是物相对X射线吸收强弱和在混合物中含量多少的反映,不对称性是样品、仪器几何条件和衍射角度、面网散射综合作用的结果.X射线单个衍射峰五个要素可广泛应用在固体材料的开发与应用研究及其它科学研究中.
参考文献:
[1]Wang H and Zhou J.Data Smoothing and Distortion of X2ray Diffraction Peak(I:Theory)[J].Journal of Applied Crystallography,2000,33.
[2]Wang H and Zhou J.Data Smoothing and Distortion of X2ray Diffraction Peak (II:Application)[J].Journal of Applied Crystallography ,2000.
[3]Scherrer P.Bestimmung der Gr sse und der inneren Struktur von Kolloidteilchen mittels R ntgenstrahlen[J].G ttinger Nachr.Math.Phys,1918,2.
[4]Wilson A J C.X2ray Optics [M].London:Methuen &Co.Ltd,1963.

