指数需求下需求与成本同时扰动的供应链协调探究

郑虹婷,陈 军

(江西师范大学鹰潭学院 教育系,江西 鹰潭 335000)

1 引言

扰动管理(Disruption Management)这个术语是由Jens Clausen、Jesper Hansen、Jesper Larsen和Allan Larsen[1]在2001年的OR/MS Today上提出的,提出后,该术语被相关研究人员广泛地接受.也引起了很多学者的关注和讨论[2-5].目前,关于扰动管理在供应链中的应用研究大多数集中于对供应链中单个因素的扰动进行管理[6、7],针对两种或两种以上的因素同时发生扰动的分析很少.但在管理实践中存在着大量多个扰动同时发生 ,或一个扰动没有结束另一个扰动就发生等更复杂的情形.作者在需求为价格的指数函数Q=De-kp条件下，需求和成本同时发生扰动时，建立了供应链模型，推导出了以下定理[8].

定理1 假设价格需求关系为Q=De-kp、市场需求从D变为D+ΔD(记作D1)、单位生产成本从c变为c+Δc(记作c1)的条件下,零售价格和生产订购数量取p*和Q*时供应链利润达到最大f*.其中最优订购量为

最优零售价格为:

供应链最大利润为：

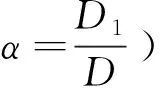
下文将在此基础之上，讨论该供应链在Stackelberg博弈理论下的协调问题.

2 需求和生产成本扰动时的供应链协调

假设供应商的利润为fs，零售商作为Stackelberg博弈的跟随者，将获得供应链利润的剩余部分fr，设供应商设定的批发价格为W，对于生产数量Q，市场需求和生产成本同时发生扰动后,供应链的总利润函数为：

(1)

供应商的利润函数为：

零售商利润函数为:

由于折扣策略经常被用于协调供应链，本文主要讨论：扰动发生后，采用不同的批发策略，使得供应商、零售商利益协调.本文中所使用的供应链协调的定义如下:

定义1[9]一个供应链称为在一个协约机制下是协调的是指通过这个协约使得供应链的最优解是供应链的组成企业决策的Nash 均衡点,即如果供应商和零售商通过追求自身收益最大化过程中也同时使得供应链的收益最大化,并且双方都不能在不损失对方的利益下获得更多利益.

数量折扣协约能实现供应链协调的一个充分条件是:

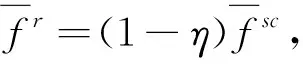
(ⅰ)当△D≥D(ekλ1+k△c-1)时供应链的协调情况

fs=ηD1e-[1+k(λ1+c1)]/k+

λ1De-(1+kc)，其中0<η<1.

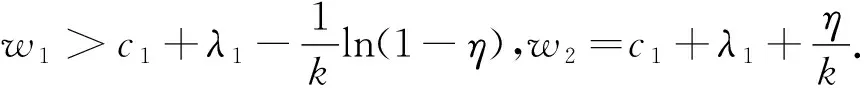
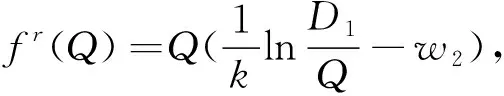
引理2 当△D≥D(ekλ1+k△c-1)且fs<λ1De-(1+kc)时，对于任意q0供应链不能够在数量折扣策略AQDP(w1,w2,q0)下达到协调.

证明 (反证)假设供应链在某个AQDP(w1,w2,q0)下得到协调．那么此时零售商应该订购Q=Q*=D1e-(1+k(λ1+c1))数量的产品才能使供应链的利润最大化，此时零售商利润为

(2)

此时供应商的利润为

(3)

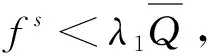
(4)

(ⅱ)当0≤△D≤D(ekλ1+k△c-1)时供应链协调情况

在这种情况下，供应链的最大值为

(5)

其中0<η<1.

同时供应商利润还可表示为：

(6)

从(5)、(6)可得w2=c+(1-η)△c+η(1+lnα)/k

定理4 若0≤△D≤D(ekλ1+k△c-1)且η如(5)式定义，下列命题成立

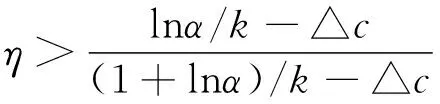
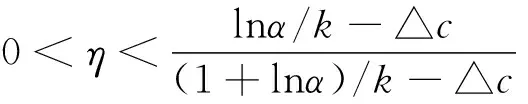
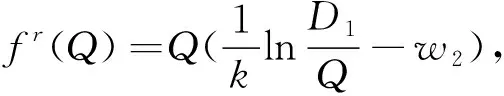
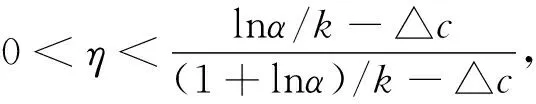
(ⅲ)当D(e-k(λ2-△c)-1)<△D<0时供应链协调情况(只考虑：△D>D(ek△c-1-1))

定理5 若D(e-k(λ2-△c)-1)<△D<0且△D>D(ek△c-1-1)，供应商利润达到fs=ηf*=ηDe-(1+kc)[(1+lnα)/k-△c]且0<η<1，则下面结论成立.

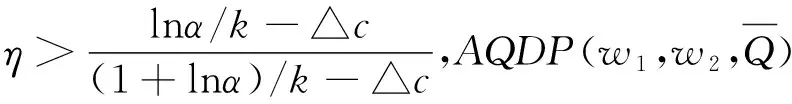
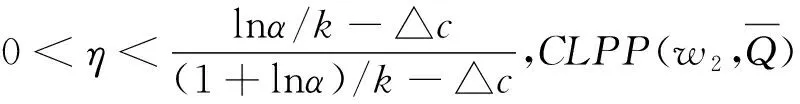
此时w2=c+(1-η)△c+η(1+lnα/k).

证明过程同第2种情况，在此省略.

(ⅳ)当△D≤D(e-k(λ2-△c)-1)时供应链协调情况(只考虑△D>D(kλ2e-k(λ2-△c)-1))设零售商利润为fr=D1e-(1+k(c1-λ2))/k-μλ2De-(1+kc))则供应商利润fs=(μ-1)λ2De-(1+kc).

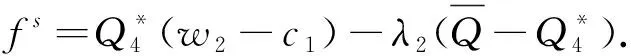
以上研究了一个协调的单周期供应链对于突发事件的最优应对策略.对于集权供应链，我们给出了它对突发事件的最优应对；对于分权供应链，我们对原有的协调协约进行了调整，使得分权供应链也能实现集权供应链对突发事件的最优应对.

参考文献：

[1]Clausen J,Hansen J,Larson J,et al.Disruption management[J].OR/MS Today,2001,28(5):40-43.

[2]Debra Elkins,Rober Handfield,Jennifer Blackhurst.Ways to guard against disruption[J].Supply Chain Management Review,2005(11/12):46-53.

[3]Lisa M Hauser.Risk-adjusted supply chain management [J].Supply Chain Management Review,2003(11/12):64-71.

[4]Uta Juttner,Helen Peck,Martin Christopher.Supply chain risk management Outlining and agenda for future research[J].nternational Journal of Logistics: Research and Applications,2003(6):197-210.

[5]Paul R Kleindorfer,Germaine H Sad.Managing disruption risks in supply chains[J].Production and Operations Management,2005,14(1):53-68.

[6]于辉,等.协调供应链如何应对突发事件[J].系统工程理论与实践,2005(7):9-16.

[7]胡劲松,等.三级供应链应对突发事件的价格折扣契约研究[J].中国管理科学,2007(6):103-107.

[8]郑虹婷.指数需求下需求与成本同时扰动的供应链模型研究[J].河南商业高等专科学校学报,2008(5):24-26.

[9]Xu M, Qi X, Yu G, et al.The demand disruption management problem for a supply chain System with nonlinear demand functions[J].Journal of Systems Science and Systems Engineering,2003,12(1):82-97.

[10]Jeuland A L,Shugan S M.Managing channal profits[J].Marketing Science,1983,2(3):239-272.