沥青路面多裂纹温度应力的数值模拟

李文成， 李郑斌， 张青军， 陈 军， 苗 雨

(1.河南省交通建设工程有限公司， 河南 郑州 450000；2.华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

沥青路面结构在形成和使用过程中，长期受到自然环境和交通荷载的作用，极易产生各种损伤。由于低温应力和重复行车荷载引起的疲劳裂缝是半刚性基层沥青路面的一个主要损伤形式，裂缝的出现严重影响了沥青路面结构的功能和使用寿命。

吴赣昌[1]等对半刚性基层中已产生贯穿裂纹时的温度应力场进行了研究，得到了裂纹应力强度因子的理论解。郑建龙等[2]对含反射裂纹沥青路面温度场的变化规律、沥青混合料的热粘弹性及路面结构中温度应力的计算进行了系统的研究。Kim J及Bozkurt D分别用三维模型阐述了反射裂纹的温度特性[3，4]；Lu等考虑沥青粘弹性因素进行了研究[5]。苗雨等[6]考虑了沥青混合料的粘弹性，利用有限元软件对含反射裂缝的沥青路面结构的温度场和温度应力进行了模拟分析。

目前大部分研究基本是对只含有反射裂缝或只含有表面裂缝的沥青路面进行分析计算，但实际上，沥青路面结构通常处在多裂纹共存的情况下。因此，本文考虑了沥青混合料的粘弹性，基于线弹性断裂力学理论，以应力强度因子为表征参量，利用ANSYS有限元软件探讨了沥青路面同时含有基层裂缝和表面裂缝时在温度荷载作用下的情况。

1 基本理论

1.1 沥青混合料的粘弹性模型

像塑料、橡胶等材料常同时具有弹性和粘性两种不同机理的形变，综合地体现粘性流体和弹性固体两者的特性，材料的这种性质称为粘弹性[7]。大量的实验研究表明，沥青混合料是一种简单热流变材料，遵从“时温等效”原理，具有明显的粘弹性特性。

Maxwell模型由弹性元件和粘性元件串联而成，如图1所示。广义Maxwell模型由多个Maxwell模型并联而成，如图2所示为四参数广义Maxwell模型。研究表明，广义Maxwell模型能较好地描述沥青混合料的松弛性能，其在参考温度t0下的应力松弛模量为：

(1)

式中，Ei、τi分别为第i个Maxwell模型弹簧的弹性模量和松弛时间，可通过试验确定。

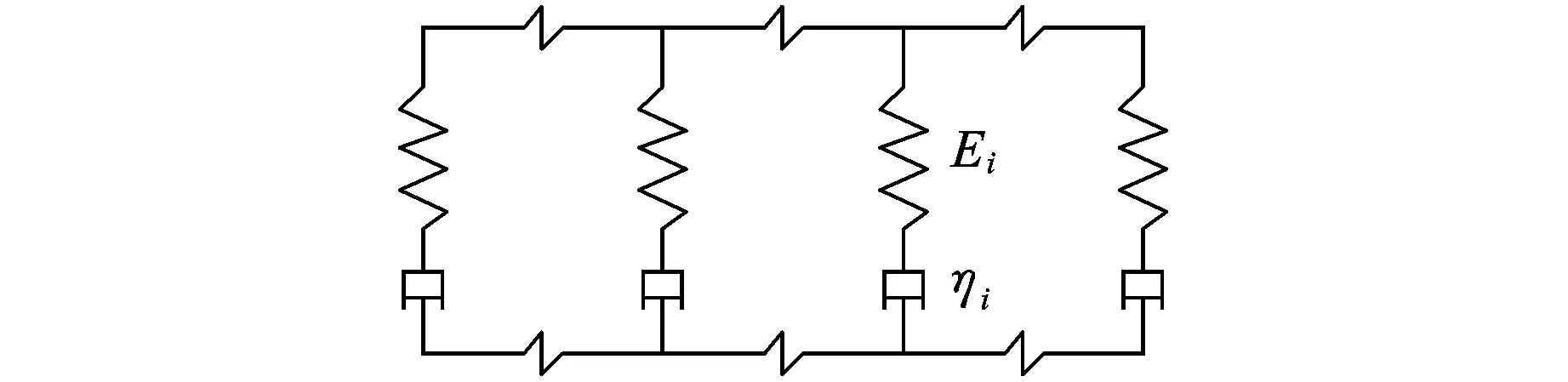
图2 广义Maxwell模型

根据Maxwell模型的本构方程、拉普拉斯变换及其逆变换，可推导出广义Maxwell模型的本构方程为：

(2)

式中，Ei、ηi分别为第i个弹性元件的弹性模量和粘性系数。

1.2 应力强度因子

用有限元法求解应力强度因子，较常用的是位移外推法[8]，即先求出裂纹前端各节点的位移，然后根据裂缝尖端应力表达式反推出K。在图3所示的裂纹尖端坐标系下，对于Ⅰ型裂纹，裂纹尖端附近的位移场可表示为：

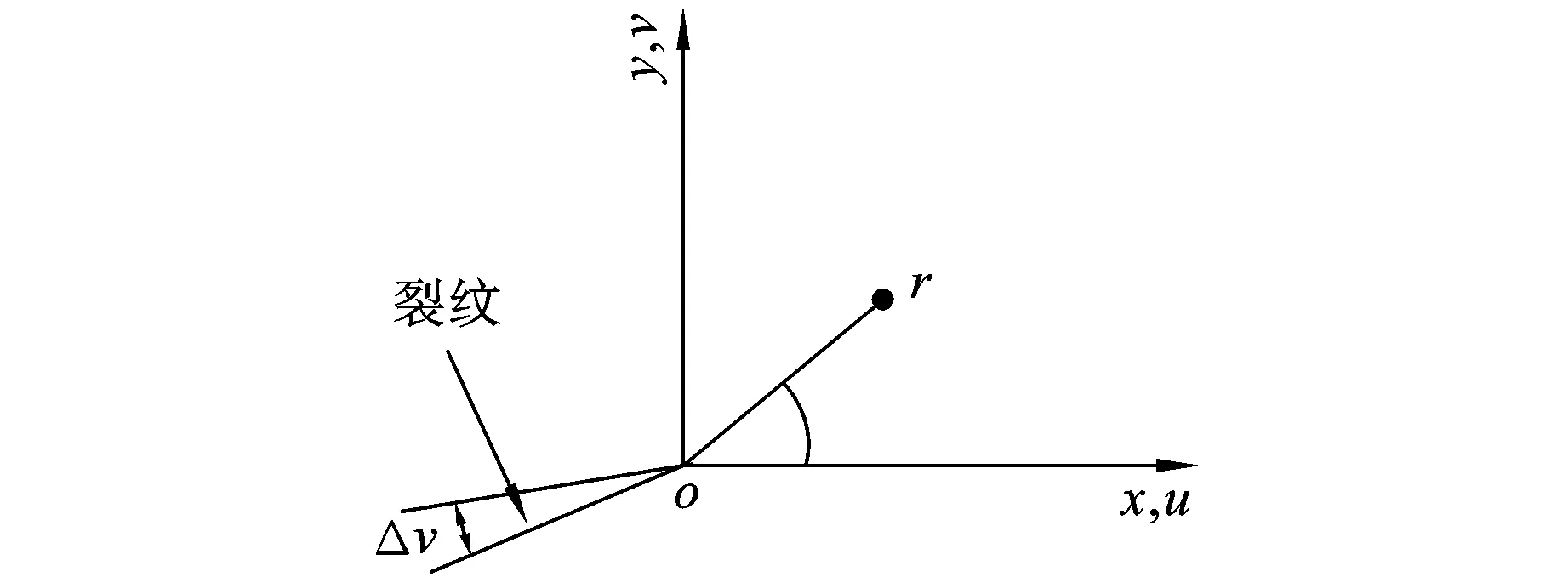
图3 裂纹尖端坐标系

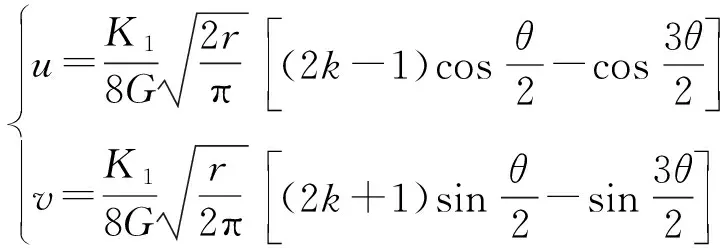
(3)

其中：G为材料的剪切模量，G=E/2(1+μ)，E为材料的弹性模量，μ为材料的泊松比；k=3-4μ(平面应变)；u和v分别为沿x轴方向和沿y轴方向的位移，是时间t的函数；K1为裂纹尖端Ⅰ型应力强度因子。同样，对于Ⅱ型裂纹，裂纹尖端位移场表达式与Ⅰ型裂纹相似：

(4)

由断裂力学可得出：

(5)

(6)

1.3 路面体系温度场分析理论

道路体系传热一般包括热传导、热对流和热辐射。由大气进入路表的气流，以热传导的方式向道路深处传导，遵循Fourier定律：

(7)

其中：q″为热流密度(W/m2)；k为导热系数(W/(m·℃))。

对于路面结构来说，长宽方向比结构层厚度大很多，可以近似视为一维热传导。而路面各层材料的导热性能相差不大，所以可以把路面简化为均质半无限体。由此，路面温度场可以由均质半无限体的一维热传导偏微分方程确定，由于路面各层材料热特性参数的不同，则对各层分别建立热传导方程，应满足下式：

(8)

其中：αi为第i层路面材料的导温系数(m2/h)。

多层路面体系之间接触良好时，接触面层间温度和热流量相等，温度函数应满足连续条件：

(9)

其中：λi为第i层路面材料的导热系数(W/(m·℃))。

路表与外界存在温差，以热对流的方式进行热交换，热对流用Newton方程来描述：

q″=h(TS-TB)

(10)

其中：h为对流换热系数；TS为固体表面的温度；TB为周围流体的温度。

由于热辐射对道路温度场变换影响较小，因此本文的计算分析忽略了热辐射的影响。

对于路面边界条件，根据实际情况和可测数据，可以利用第2类、第3类边界条件。第2类边界条件为已知进入路表的热流函数q(t)，满足条件式为：

(11)

而对于另一项无限深处的边界条件则须满足有界条件：z→∞,T(∞,t)≠∞。第3类边界条件为已知大气温度随时间变化的函数f1(t)，满足条件式为：

(12)

由于大气温度随着时间不断变化，道路温度场研究是一个典型的瞬态分析过程，初始温度条件可以由稳态热分析得出。稳态热分析的能量平衡方程为：

[K]{T}={Q}

(13)

其中：[K]为传导矩阵，包含导热系数、对流系数及辐射率和形状系数；{T}为节点温度向量；{Q}为节点热流率向量，包含热生成。瞬态热平衡可以表达为：

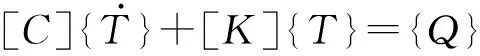
(14)

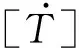
2 数值算例

利用ANSYS软件研究沥青路面结构中含有表面裂缝和基层底面裂缝时的情况，沿行车方向取一个长为15 m的平面应变模型作为计算模型，如图4所示，基层底面裂缝长10 cm，位于x=7.5 m处，表面裂缝位于基底裂缝右侧，长4 cm，与基层裂缝水平间距为d。半刚性基层沥青路面结构各层参数见表1，沥青层粘弹性参数见文献[9]。本文在初始温度为0℃，降温速度为5℃/h的条件下，利用ANSYS分别对表面裂缝和基层底面裂缝不同间距下的沥青路面进行热-结构耦合分析。

图 4 含多裂纹沥青路面有限元计算模型

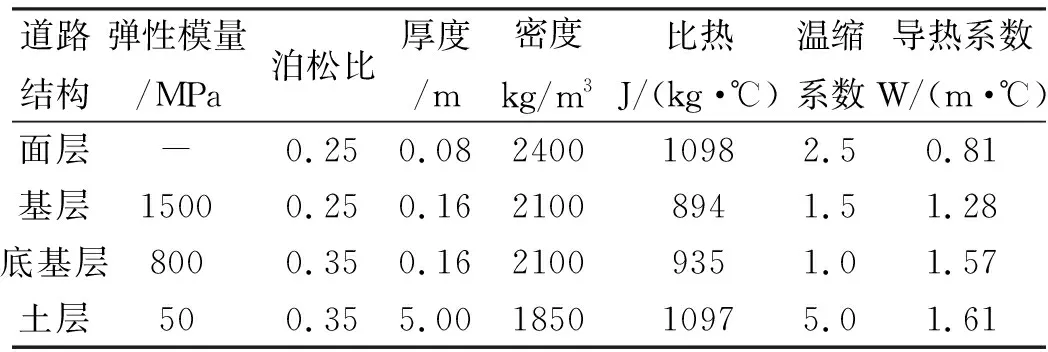
表1 路面结构各层参数

计算基本假定：

(1)沥青混合料面层视为线粘弹性材料，采用广义Maxwell模型模拟其粘弹性；其余的各层均视为线弹性 (裂纹部分除外)；

(2)道路结构各层间位移连续；

(3)各层路面接触良好，位移连续，热传导连续，忽略热辐射的影响。

2.1 一次降温条件下道路体系温度场情况

如图5所示，不同裂纹间距下，基层底面裂缝的I型应力强度因子K1随移动荷载位置的变化趋势相似：K1随移动荷载靠近基底裂缝而逐渐增大，当移动荷载位于基底裂缝正上方，即荷载中心位于7.5 m处时，K1值达到最大，随后随着移动荷载远离基底裂缝K1逐渐减小。在初始温度为0℃，降温幅度为5℃/h的条件下，研究6 h的降温情况。图5为表面裂纹与基层裂纹间距为0.0 m时的道路温度场情况，可以看出：路表附近曲线下降剧烈，温度降低很快，随着深度的增加，温度曲线逐渐平直，降温趋势逐渐缓和，即外界温度对道路体系的影响在路表附近较为显著，随着深度增加，影响逐渐减小，在深度超过30 cm后，几乎不再受外界温度影响。

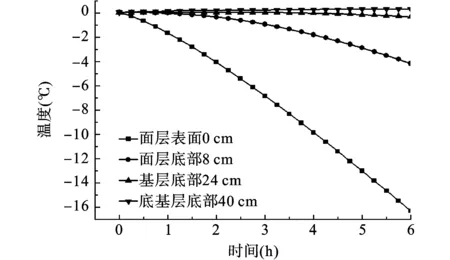
图5 裂缝间距为0 m时道路温度场

2.2 裂缝间距对基层底面裂纹应力强度因子的影响

在初始温度为0℃，降温幅度为5℃/h的条件下，利用ANSYS对含多裂缝的沥青路面进行热-结构耦合分析。图6为裂缝间距为0 m时，基层底面裂缝应力强度因子随时间变化的曲线。由此可知，随着温度的降低，由温度应力导致的基底裂缝I型应力强度因子K1明显增大，表明低温更易导致裂缝扩展。相同条件下，对只含有基层裂缝的路面结构进行计算得出的K1值为17479.5 Pa·m1/2。图7所示为温度降幅30℃时，K1随裂缝间距变化的曲线，随裂缝间距的增大K1先增大后减小并趋于稳定，其值与只含基层裂缝时的K1值相当，可见，随着裂缝间距增大，表面裂缝对基层底面裂缝的影响逐渐减小直至可以忽略。

图6 裂缝间距为0 m时I型应力强度因子K1变化曲线

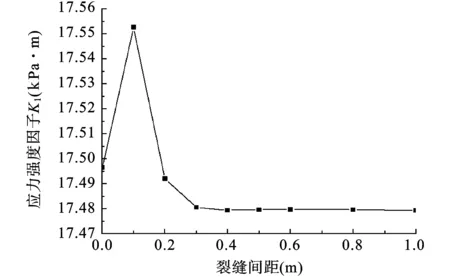
图7 K1随裂缝间距变化的曲线

2.3 裂缝间距对表面裂缝的影响

通过计算分析可知，当裂缝间距小于0.5 m时，随着温度降低，表面裂纹尖端拉应力逐渐增大；而当裂缝间距大于0.5 m时，随着温度降低，表面裂纹尖端的拉应力逐渐变为压应力，如图8所示。随着裂纹间距的增大，表面裂纹尖端的最大拉应力呈现先增大后减小的趋势，如图9所示，这是因为在裂纹间距较近时，基层裂纹的存在影响了表面裂纹处的应力分布。

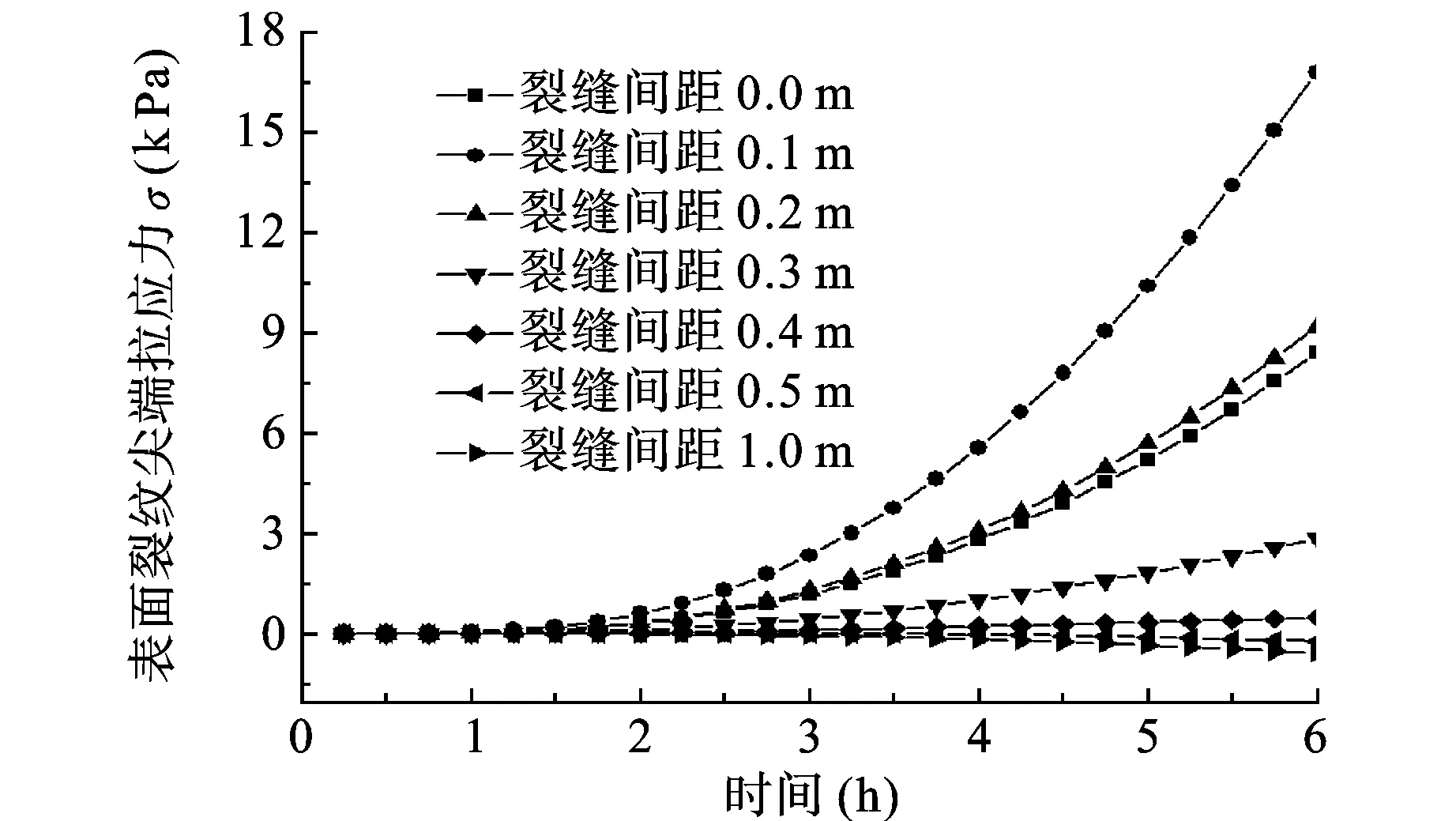
图8 不同裂纹间距下表面裂纹尖端应力变化曲线

图9 表面裂纹尖端最大拉应力随裂缝间距变化曲线

2.4 采用土工布防治裂缝

土工布具有抗拉强度高、延伸率适中、保温作用好等特点，因此在沥青面层与基层之间加铺土工布成为防治反射裂缝的一种有效措施。本文对表面裂缝与基底裂缝间距为0.1 m，沥青面层和基层之间加设土工布后的模型进行了有限元分析。由图10和图11可以看出，加铺土工布能够有效地降低基层裂纹尖端的应力强度因子和表面裂纹尖端的拉应力，从而能够延缓反射裂缝的形成，延长路面使用寿命。

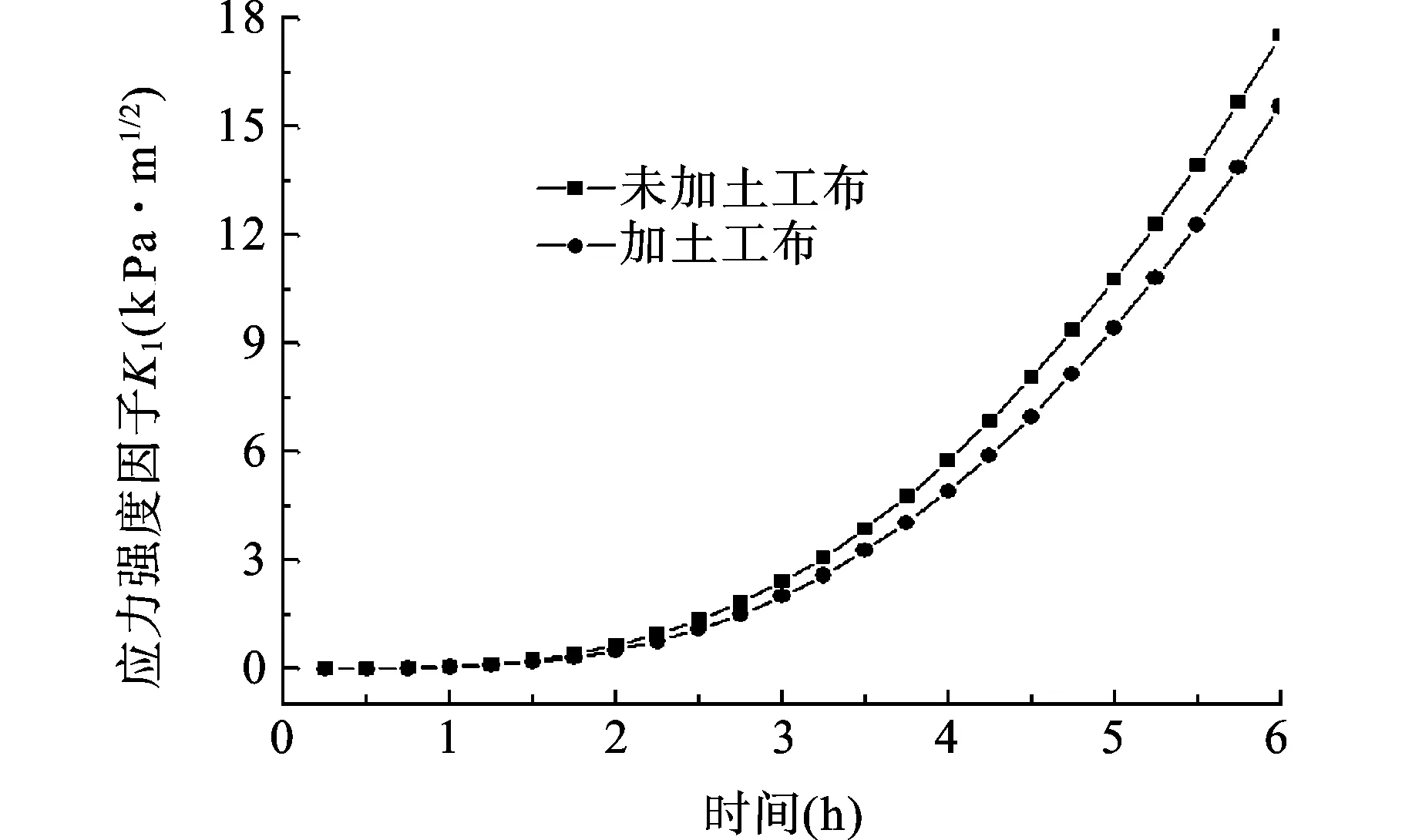
图10 加铺土工布前后基层裂纹应力强度因子对比

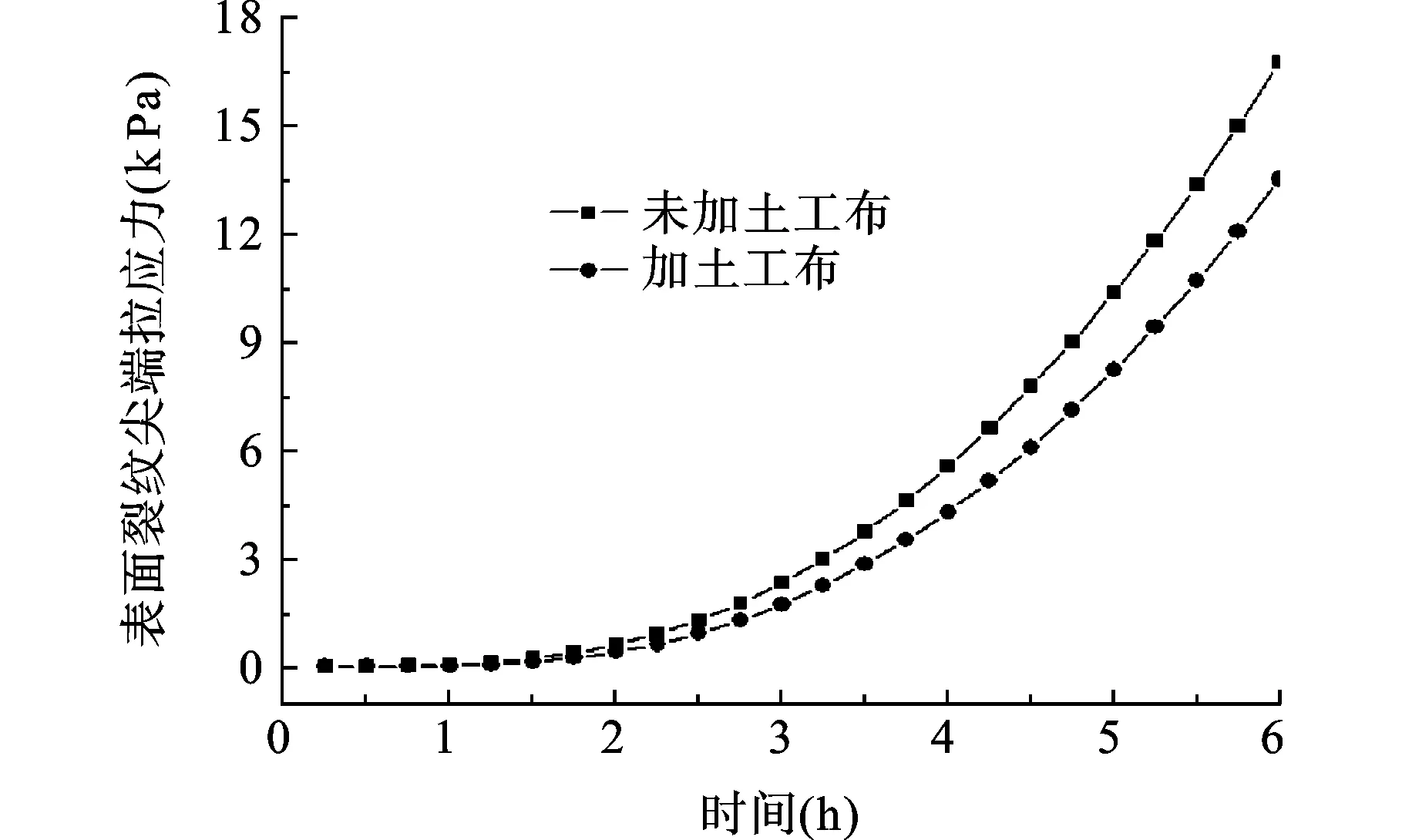
图11 加铺土工布前后表面裂纹尖端拉应力对比

3 结 论

(1)随着温度降低，基底裂缝的I型应力强度因子K1逐渐增大，说明低温更易导致裂缝扩展。裂缝间距小于0.1 m时，表面裂缝对基底裂缝影响明显，导致K1增大；之后随裂缝间距的增大，表面裂缝的影响逐渐减小。

(2)当裂缝间距小于0.5 m时，随着温度降低，表面裂纹尖端拉应力逐渐增大；而当裂缝间距大于0.5 m时，随着温度降低，表面裂纹尖端的拉应力逐渐变为压应力。随着裂纹间距的增大，表面裂纹尖端的最大压应力呈现先增大后减小的趋势。

(3)沥青面层与基层之间加铺土工布，可以有效地延缓裂缝扩展，延长路面使用寿命。

[1] 吴赣昌.半刚性路面温度应力分析[M]. 北京：科学出版社，1995.

[2] 郑建龙, 关宏信. 温缩型反射裂缝的热粘弹性有限元分析[J]. 中国公路学报,2001,14(3):1-5.

[3] Kim J. Three-dimensional finite element modeling of multi-layered systems comprehensive nonlinear analysis of rigid pavement systems [D]. Chicago: University of Illinois at Urbana-Champaign,1999.

[4] Bozkurt D. Three dimensional finite element analysis to evaluate reflective cracking potential in asphalt concrete overlays[D]. Chicago: University of Illinois at Urbana-Champaign, 2002.

[5] Lu Y, Wright P J.Temperature related visco-elastoplastic properties of asphalt mixtures[J]. Transportation Engineering, 2000, 126(1): 58-65.

[6] 苗 雨, 万云冬, 董玉凯. 沥青路面反射裂纹温度应力的数值模拟[J]. 岩土力学, 2007, 28(s1):343-347.

[7] 杨挺青.粘弹性力学[M]. 武汉: 华中理工大学出版社, 1990.

[8] 程 靳, 赵树山.断裂力学[M]. 北京:科学出版社, 2006.

[9] 钱国平, 郭忠印, 郑建龙,等. 环境条件下沥青路面热粘弹性温度应力计算[J]. 同济大学学报(自然科学版),2003,31(2):150-155.

[10] JTG D50-2006, 公路沥青设计规范[S].