大跨斜拉桥在移动荷载作用下的振动控制
万信华
(中铁第四勘察设计院集团有限公司,湖北 武汉 430063)
调质阻尼器(TMD)由于其结构紧凑、价格经济、使用方便,已开始用于桥梁工程的振动控制中。单调质阻尼器(STMD)对窄带的激励有较好的控制效果,而且其控制效率在阻尼器质量和阻尼一定的条件下,对阻尼器与受控系统之间的频率比非常敏感[1]。只有在最优频率比附近,控制效率才达到最优,一旦频率漂移,其控制效率将大大下降,甚至起到相反作用[2]。在桥梁工程中,由于结构、材料等因素的变异特征,其基本频率均会在一定程度上产生漂移,无论是在车辆荷载或是在风荷载作用下,用STMD控制结构的振动往往难以达到理想的效果。
多重调质阻尼器(MTMD)是由多个具有不同频率、不同质量或不同阻尼的调质阻尼器构成的动力吸振器群,被广泛应用于结构的被动控制中。本文以一座大跨斜拉桥为例,研究多重调质阻尼器(MTMD)对结构在汽车荷载作用下的振动控制。在结构动力模态分析的基础上,研究结构振动控制振型及其对应的固有振动频率,建立包含结构振动控制振型及MTMD系统的运动方程,以结构跨中位移动挠度为控制目标对MTMD参数进行分析和优化,然后按常规有限元方法对车-桥-MTMD系统进行动力时程分析,验证MTMD控制结构竖向振动的有效性。
1 振动控制振型幅频响应方程
假设在某斜拉桥结构跨中区域安装n个TMD(图1),MTMD的频率以结构振动控制振型频率为中心按一定间隔等间距分布,n为奇数。第i(i=1,2,…,n)个TMD的质量为mi,刚度和阻尼常数分别为ki、ci,与主体结构的竖向相对位移为vi,绝对位移为zi。则第i个TMD的运动方程:

图1 具有MTMD的斜拉桥平面模型(标注单位:m)
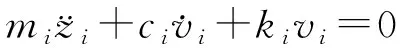
(1)
斜拉桥结构运动方程:
(2)
式中,[MC]、[CC]、[KC]分别为主体结构的质量矩阵、阻尼矩阵和刚度矩阵;{x}为主体结构的位移列向量;{F1(t)}为汽车荷载对主体结构的作用,由于汽车作用与随机的桥面不平顺有关,因此将{F1(t)}看成一个随机荷载;{F2(t)}为MTMD对主体结构的作用,只有在布置TMD的节点沿竖向自由度方向有非零值。
(3)
设斜拉桥结构振动控制振型列向量{Φ}={φ1φ2…φm}T,其中下标m为主体结构的总自由度数。另有振型子向量{φ}⊂{Φ},{φ}={φj1φj2…φjn}T,它的每个元素表示n个TMD位置处的振型幅值。
由于控制振型的贡献相对占优,于是可近似认为
{x}={Φ}q
(4)
式中,q为结构振动控制振型坐标。设xji表示主体结构第i个TMD位置处的竖向位移,则有vi=zi-xji,xji=φjiq,得
vi=zi-φjiq
(5)
将式(4)代入式(2),并等式两边左乘{Φ}T,有
(6)
式中,M、C、K分别为主体结构振动控制振型的广义质量、广义阻尼和广义刚度,且M={Φ}T[MC]{Φ}、C={Φ}T[CC]{Φ}、K={Φ}T[KC]{Φ}。
将式(5)代入式(3),并将{F2(t)}表达式代入式(6),得到
(7)
将式(5)代入式(1),有
(8)
联立方程式(7)和式(8),得到结构振动控制振型和n个TMD构成新系统的动力平衡方程为:
(9)
式中,
{Y(t)}={qz1z2…zn}T
(10)
{P(t)}={ΦTF1(t) 0 0 … 0}T
(11)
(12)
[CS]=
(13)
[KS]=
(14)
为了求得频率响应方程,令{F1(t)}={Fm}e-iωt,其中{Fm}为各点激励幅值组成的列向量,根据线性定常系统的保频性,有
{Y(t)}={y(ω)}e-iωt
(15)
{y(ω)}=([KS]-ω2[MS]-iω[CS])-1{ΦTFm0 … 0}T
(16)
由于[MS]、[CS]、[KS]仅在第一行、第一列和对角线上有非零元素,结构控制振型的广义坐标幅频响应q(ω)为{y(ω)}的第一元素。先对矩阵求逆,而后可得q(ω)
q(ω)=
(17)
不失一般性,假定在随机不平顺桥面条件下,汽车荷载对桥梁的激励为功率谱密度函数为S0的白噪声,根据方差的定义,结构振动控制振型主坐标q的方差[3]
(18)
显然,只有|q(ω)|小,σq才能取得小值,因此将|q(ω)|min作为MTMD参数优化的条件。
2 大桥动力模态分析
由前述论证可知,用MTMD控制结构的振动,必须针对结构振动的某一具体振型,对于结构跨中动挠度,该振型要在所有振型贡献中占优,为此,必须先对结构进行动力模态分析。下面以湖北省境内某大跨斜拉桥为例,以结构跨中动挠度为控制目标,阐述结构振动控制振型坐标幅值|q(g)|与各自变量的关系,主桥桥型布置如图2,有限元分析模型如图3。
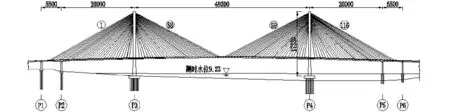
图2 桥型布置

图3 主桥有限元动力分析模型
主要材料和力学性能如表1,有限元模型没有考虑桥梁纵坡的影响,主梁、主塔采用6自由度梁单元,斜拉索采用2自由度杆元,使用公式修正弹性模量考虑拉索垂度的非线性效应。全桥共有217个节点,116个杆元,214个梁元。对主桥结构进行动力特性分析,得到各阶频率和相应振型,部分低阶频率和振型描述如表2。
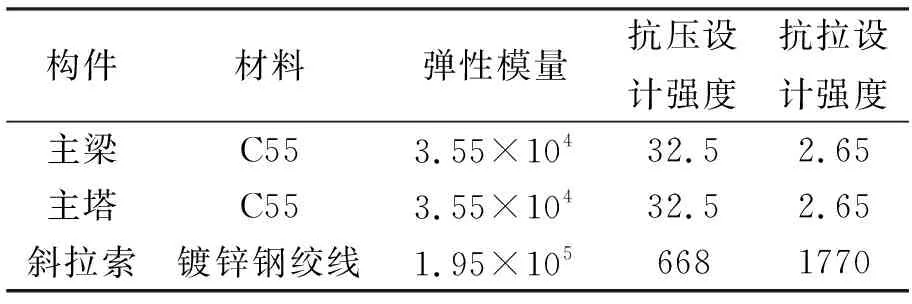
表1 结构材料和力学性能 MPa

表2 成桥状态主桥结构振动模态
由振型分析可知,斜拉桥跨中竖向振动主要是一阶对称弯曲振型的贡献(图4)。

图4 主桥一阶对称弯曲振型,频率0.093
3 MTMD参数分析与设计
MTMD的频率以结构振动控制振型的频率为中心等间距分布,为了便于加工和制作,每个TMD采用相同的质量和阻尼比,刚度和阻尼常数随频率发生变化。第i个TMD的参数可表示为

ci=2miωiξi(i=1,2,…,n)
(19)

设有变量g定义为无量纲的频率比,g=ω/ωc,其力学意义是汽车激励频率与结构振动控制振型频率之比。
将上述各参数代入式(17),并经整理得
(20)
其中
Z(g)=
(21)
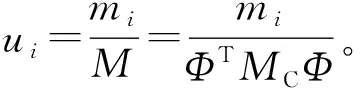
由式(20)和式(21)可知,结构振动控制振型坐标幅值|q(g)|是一个多自变量的函数,它与外荷载的激励频率与结构振动受控振型的频率比g、MTMD的个数n、阻尼比ξi、质量比ui以及反映MTMD频率间隔的量β等参数有关。
下面针对主桥结构对称弯曲振型,研究MTMD各参数对振型坐标幅值的影响。
3.1 平均阻尼比ξT的影响
平均阻尼比ξT定义为MTMD的中心频率对应的阻尼比,在本题目中,实际上为各TMD的阻尼比ξi,因为假设各TMD的阻尼比相同。
图5中各条曲线无一例外反映了幅值响应随MTMD阻尼比增大而增大的趋势,先是呈直线上升,而后过度进入平缓上升阶段。这说明MTMD阻尼的存在,抑制了MTMD自身的振动,从而削弱了对主体结构的控制作用,所以各TMD阻尼愈小控制作用愈明显。设计和制作TMD时,由于对空间和作动位移的限制,TMD要有一定的阻尼,但阻尼比应在5%以内。图5同时反应了幅值响应随TMD数量增多而减小的趋势,但趋势是减弱的。
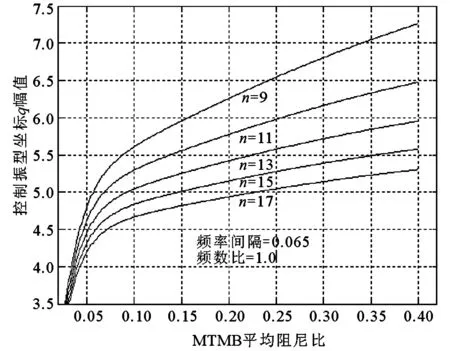
图5 ξT与q幅值关系曲线

图6 频率间距与q幅值关系曲线
3.2 MTMD频率间距的影响
从图6可以看出,优化频率间距在0.055~0.065附近,超出此范围幅值响应均会增大,同时还反映了幅值响应随阻尼比减小而减小的趋势。
3.3 MTMD广义质量比ui的影响
图7表明,当各TMD质量比在1%以内变化时,幅值响应急剧减小,超出此范围仍有减小的趋势,但十分平缓。从理论上说,控制结构的动力响应,TMD的质量做得愈大愈好,但同时增加了主体结构的静力负荷,因此理想的TMD广义质量比应在1%~2%之间。
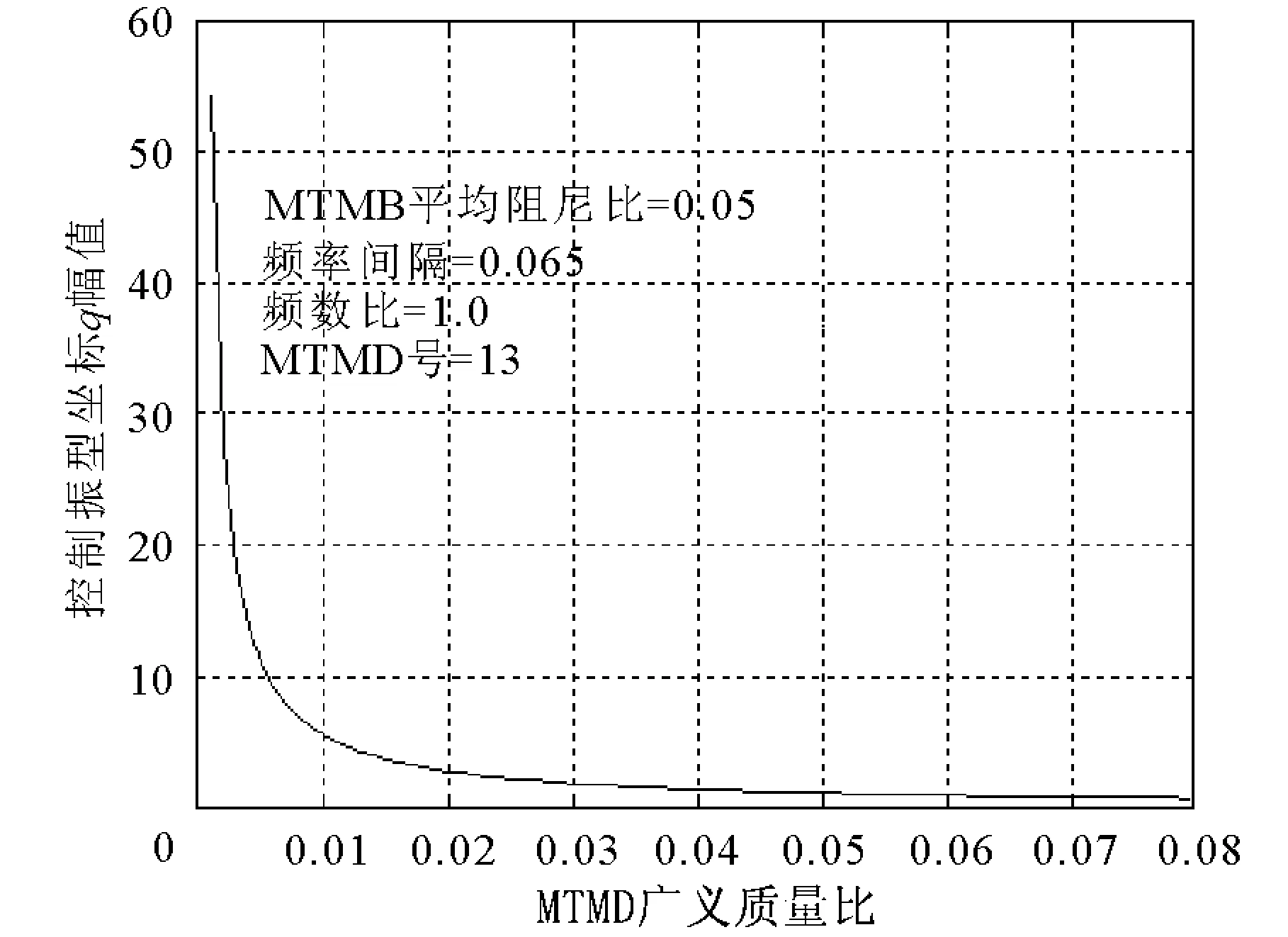
图7 ui与q幅值关系曲线
3.4 MTMD数量n的影响
图8反映的是当TMD广义质量比ui=0.015时,各种数量的MTMD以及无TMD情况下结构振动控制振型坐标q的幅频响应。研究表明,振型坐标峰值随TMD数量增多而减小,增多到一定程度后,这种减小的趋势已经变得很弱,但波峰之间的频率差变得更大,这就意味着MTMD控制结构的频带变得更宽,表明了MTMD对各种激励频率较强的适应能力。
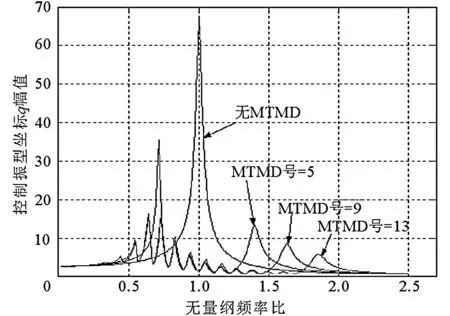
图8 MTMD数量n对q幅频响应的影响
3.5 MTMD布置间距的影响
图9是5个TMD当以不同间距布置在结构跨中区域时,结构振动控制振型坐标q的幅频响应。结果表明,MTMD布置得越紧凑,MTMD控制结构的能力越强。
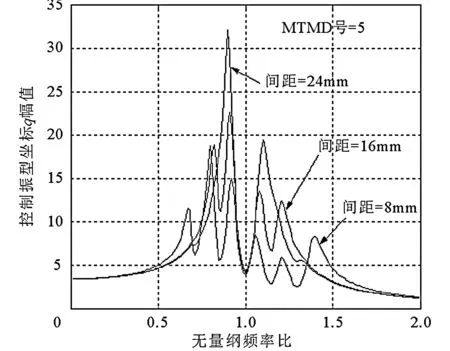
图9 MTMD布置间距对q幅频响应的影响
通过对主桥结构振动控制振型坐标的频域分析,不难确定MTMD控制系统的参数,经综合考虑:选定TMD的数量为13,集中对称布置在结构跨中的一个区域(图1),MTMD中心频率为0.584 rad/s,频率间距为0.065 rad/s,每个TMD广义质量比为1%,阻尼比0.03,每侧布置间距8 m,由此可得各TMD阻尼常数和刚度常数。
4 车-桥-MTMD系统动力时程分析
为了验证MTMD的制振效果,再用常规有限元方法对MTMD控制下的车桥耦合系统进行动力时程分析(关于车桥耦合系统动力分析的理论与方法,作者已另文讨论)。考虑桥面的随机不平顺,计算了6辆汽车分别以80 km/h和100 km/h并排过桥时,主桥跨中位置的动挠度时程曲线,并和无MTMD时的同样情形相比较。从图10中可以清晰看出,MTMD明显地改变了结构的时程响应,使动力峰值反应分别减小约29%和25%,但在最初的一段时间内,MTMD对时程响应改变很小,分析其原因,是因为MTMD从0初始速度到充分振动需要一个时间过程。

(a) 汽车速度80 km/h
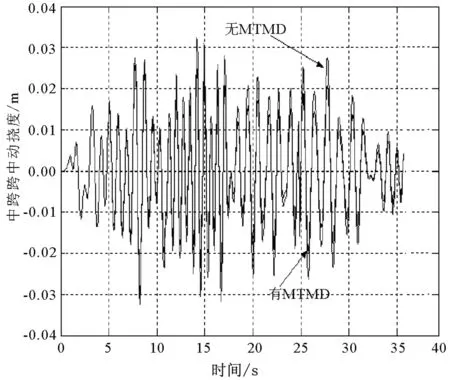
(b) 汽车速度100 km/h图10 主桥跨中动挠度时程曲线
5 结 论
以结构振动理论的频域分析方法为基础,考虑MTMD在多自由度结构中的位置,推演了具有MTMD的MDOF结构振动受控振型广义坐标频率响应方程,在此基础上,以大桥跨中位移动挠度为控制目标对MTMD参数进行优化设计。研究结果表明:
(1)MTMD参数优化必须针对结构振动控制振型,不同的结构或是同一结构的不同振型,MTMD的优化参数会不同。
(2)主桥结构对称弯曲振型坐标幅值随TMD个数、广义质量比的增加而减小;随阻尼比减小而增大;理想的频率间距在0.055~0.065之间;MTMD在结构跨中布置得越紧凑,对结构的控制效果越好。
(3)时程分析表明,只要MTMD参数设计恰当,它就可以有效减小结构在移动荷载作用下的动力响应。
[1] 陈艾荣,项海帆.多重调质阻尼器制振性能及对桥梁抖振的控制[J].同济大学学报(自然科学版),1998,26(2):125-129.
[2] 余钱华,胡世德,范立础.桥梁结构MTMD被动控制的理论研究和实桥分析[J].世界地震工程,2001,(3):105-108.
[3] 丁文镜.减振理论[M].北京:清华大学出版社,2005.
[4] 阎维明,周福霖,谭 平.土木工程结构振动控制研究进展[J].世界地震工程,1997,13(2):8-18.
[5] 彭 刚,张国栋.土木工程结构振动控制[M].武汉:武汉理工大学出版社,2002.
[6] 曾宪武,韩大建.大跨桥梁风致抖振时域分析及在ANSYS中的实现[J].桥梁建设,2004,(1):11-14.
[7] 高 伟.随机、智能结构随机振动分析与主动控制研究[D].西安:西安电子科技大学,2003.
[8] 聂润兔,邵成勋,邹振祝.智能桁架机电耦合动力分析与振动控制[J].振动工程学报,1997,10(2):119-124.

