某大型沉井基础关键施工过程受力分析
杨灿文, 黄民水
(1. 中铁大桥勘测设计院有限公司, 湖北 武汉 430056;2. 武汉工程大学 交通研究中心, 湖北 武汉 430073)
随着国内大跨度桥梁不断的涌现,沉井由于其刚度大、经济性好的特点,越来越多地应用于桥梁深水基础和悬索桥锚碇基础。其中1999年建成的江阴长江公路大桥南锚碇采用平面尺寸51 m×69 m,高为58 m的矩形沉井基础,为国内最大的锚碇沉井基础[1,2];目前在建的泰州长江公路大桥中塔采用水中沉井基础,平面尺寸为58.4 m×44.4 m,高为76 m,其中下层44 m为钢结构,上层32 m为钢筋混凝土结构,为国内最大的水中沉井基础[3]。
目前对于大型沉井基础施工过程的研究,更多的关注沉井的下沉和施工控制[4~6],而对于沉井的本身结构受力一般采取平面的简化计算,计算方法偏于保守,往往造成设计的浪费,并且未能反应沉井的实际受力状况。本文对某锚碇的大型沉井基础关键施工过程进行了平面简化和实体有限元计算,对大型沉井基础的关键施工阶段进行受力分析研究,获得了一些有价值的结论。
1 沉井简介
该沉井如图1所示,沉井长和宽分别为60.2 m和55.4 m,沉井高41 m,共分八节,第一节高8 m;第二到六节为5 m高,第七节为3.5 m,第八节为4.5 m。井内共设置25个井孔,第二节壁厚2.4 m,第三到七节壁厚2.2 m;隔墙厚2.2 m;刃脚高1.8 m,底部设置0.2 m厚的踏面,隔墙底部比井壁底部高1.8 m。沉井封底混凝土厚为8 m。沉井基础处地表覆盖层厚约45 m,以砂层为主,自上而下依次为可塑状粉质粘土、流塑状淤泥质粉质粘土、稍密状~中密状粉细砂及中密状中砂。基底置于中密的中砂层。
2 计算工况及模型
在沉井施工的过程中,主要有两个关键步骤,第一个是沉井初始下沉阶段,在沉井第一、二节现场预制完成后,抽取隔墙和刃脚底部的垫木,从井孔中心取土下沉;第二个是沉井下沉到设计高程后,在沉井封底之前,将沉井井底部完全掏空。在第一个施工阶段,沉井受力出现体系的转换,由于沉井隔墙底部土体掏空,沉井受力为均匀作用于井壁和隔墙底部的支撑垫木上转换为由仅井壁底部进行竖向支撑;这时沉井侧壁还没有出现土体摩阻力,自重完全由隔墙和刃脚底部承受,此时隔墙底部受拉,应力最大。在第二个施工阶段,在井外土压力作用下,沉井底部刃脚及刃脚以上井壁受最大的水平土压力。下面就将这两个关键的施工步骤作为两个工况进行分析。
结构计算采用商业软件Midas Civil,空间模型采用实体单元,有限元模型如图2所示。沉井结构材料为C30混凝土,容重为25 kN/m3,弹性模量为3×107kPa。考虑沉井的对称性,选取1/4结构进行空间分析[7]。

图1 沉井基础结构布置

图2 沉井有限元实体模型
对于工况一,由于结构仅在刃脚支撑,若采用平面模型,可考虑简化为一个方向支撑的梁,但从沉井的平面尺寸看,长边与短边的比值大于1而小于2,因此在自重作用下,沉井为双向受力结构,采用单向的简化计算并不合适;为反映实际的受力情况,将底部两节建立1/4的空间实体模型,在沉井的刃脚踏面施加竖向和水平约束,在对称中心施加对称约束,计算荷载仅考虑自重。其中对于竖向约束,考虑井壁的刃脚是直接支撑在地基上,因此需采用弹性支承模拟;但实际施工时,为保证沉井预制时的稳定,对地基进行了加固,所以地基的竖向弹性支承刚度较难取值;为比较地基刚度对沉井受力的影响,将竖向支撑分别按照固结、20000 kN/m(节点弹性支承)、10000 kN/m进行约束。
对于工况二,传统简化计算根据《公路桥涵地基与基础设计规范》相关规定进行。在进行竖直方向的检算时,刃脚沿周长方向取单位宽度(1 m),计算荷载考虑沉井自重和刃脚的水土压力(图3),此时沉井刃脚向内弯曲,刃脚根部截面外侧受到最大的拉应力,控制刃脚根部的配筋;在进行平面计算时,选取刃脚根部以上高度等于刃脚宽(2.0 m)的一段井壁进行平面框架检算,计算荷载取作用在井壁上的水土压力,其中该水土压力包括2 m井壁高内的水土压力和刃脚根部传递过来的水平力,此时井壁在平面内受力最大,控制沉井根部水平方向的配筋;平面计算软件仍采用Midas Civil,井壁和隔墙均用梁单元模拟,计算荷载取水土均布压力,为750 kN/m,计算模型如图4所示。

图3 沉井井壁水土压力分布
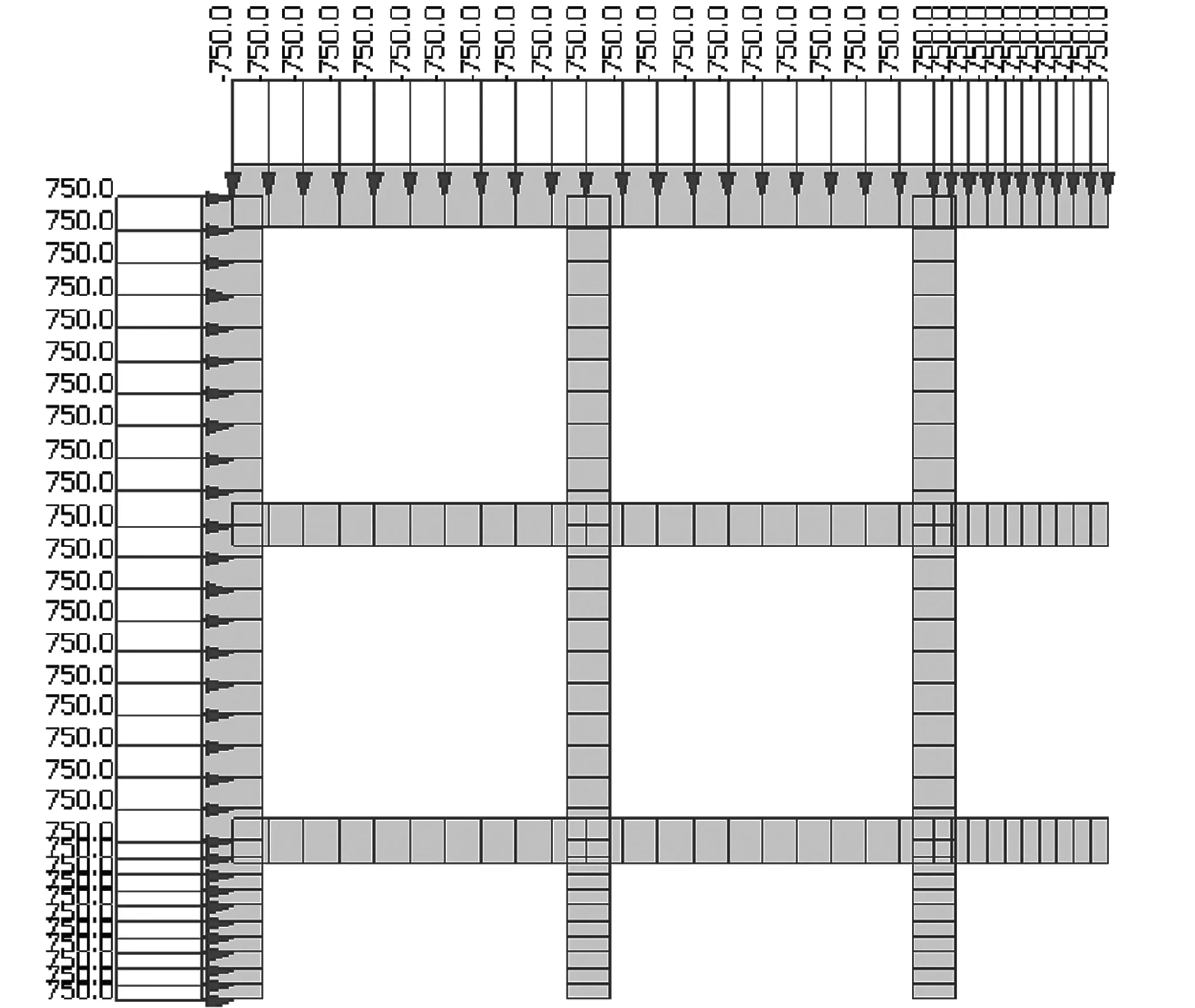
图4 刃脚根部井身框架平面计算模型
相应工况二的空间计算模型取1/4的沉井全模型,如图2所示,对称中心施加对称约束,考虑在沉井下沉到位后,沉井在周边土体摩阻力的作用下不再继续下沉,因此在沉井井壁外周边施加竖向弹性约束,约束的刚度取一个较大值以更好的模拟沉井受力。沉井荷载考虑沉井自重和外壁水平水土压力,其中水土压力采用水土分算,土体取浮重10 kN/m3,内摩擦角按照砂土取30°,水平土压力侧压系数λ=tan2(45°-φ/2);水压力考虑沉井内外水头差5 m考虑,计算水土压力按线性分布[8,9],如图3。
3 计算结果分析
3.1 工况一
工况一的计算结果如表1和图5所示。

表1 工况一计算结果

图5 工况一实体模型主拉应力云图(刃脚竖向固结,kN/m2)
通过计算,隔墙底部最大拉应力出现在中间隔墙底部;最大压应力出现在中间隔墙与井壁相交的底部,计算结果与定性判断一致,即计算结果基本反应了实际的受力情况。
比较沉井刃脚竖向固结和竖向弹性约束的计算结果,可得到随着刃脚底部地基土体刚度的降低,沉井的主拉应力逐渐减小,相应位移逐渐增加;由此可见,随着土体的刚度降低,沉井整体发生沉降,而竖向力(自重)对隔墙和井壁的作用内力分配不断改变,隔墙弯矩逐渐减小,井壁受力逐渐增加。可见,在对沉井的地基进行加固时,加固后地基强度大虽然对沉井预制时保持稳定有一定好处,但对沉井本身的受力并不是很有利;因此在施工时除满足基本要求外,地基的加固强度不需要太高。
同时,也可以看到,三种约束情况计算的沉井所受最大主拉应力相差仅在10%以内,在进行沉井隔墙的结构设计时,可以偏安全的选取刃脚竖向固结的情况作为控制,以避开对地基支承刚度的选择问题,也不会消耗过多的材料。
3.2 工况二
工况二按简化方法计算竖向刃脚受力,计算结果如表2,平面弯矩分布如图6所示。

表2 工况二平面计算结果

图6 工况二底节框架平面计算弯矩(kN·m)
实体单元计算结果如图7和表3所示。

图7 工况二实体模型计算结果

荷载拉应力/MPa位置自重+土压力1.036中间隔墙底部水平拉应力土压力0.488沉井上端变截面处水平拉应力0.385刃脚根部以上2 m处水平拉应力0.292刃脚根部竖向拉应力
通过实体计算,在自重+土压力的荷载作用下,水平方向的最大拉应力为1.036 MPa,出现在沉井中部的隔墙底部。比较初始下沉时的2.849 MPa隔墙拉应力,减小许多。随着沉井的逐渐下沉和不断接高,中间隔墙的抗弯惯性矩逐渐增大,而井壁所受的水平土压力也逐渐增加,其对隔墙产生的轴向力逐渐增大;在自重和水平土压力的作用下,隔墙底部拉应力逐渐减小,由此可见,对隔墙初始下沉时底部拉应力最大的判断是准确的。
为比较工况二平面计算与实体计算的结果,在实体计算时,仅考虑沉井在承受水土压力作用下的受力。根据计算可得到最大拉应力出现在沉井上端变截面处。分析原因,沉井上端4 m范围内没有隔墙的支撑作用,在平面上看就是一个大的矩形框架;因此,在水平压力作用下,井壁在支撑变化处出现较大的变形,计算得到该处相应水平拉应力为0.488 MPa。
而与平面框架计算相对应的井壁处,由于此处同样为隔墙支撑的变化处,也出现较大的应力,最大水平拉应力出现在纵横向井壁的交界处,相应值为0.385 MPa,仅为平面计算的22%。分析原因,主要有两个:第一是在平面计算时仅取2 m高的一段井壁进行计算,该段和刃脚的土压力均作用在这部分井壁上,未考虑刃脚和上端井壁的水平框架作用对水平土压力的分配;也就是说,该段平面计算的水平土压力可以不考虑刃脚的提供的水平力。第二个原因是计算将井壁和隔墙均按梁单元进行简化,与实体单元的计算比较,变形增大许多,相应拉应力也较大。
计算在土压力作用下井壁的竖向拉应力,可得到刃脚根部相应最大拉应力为0.292 MPa,比简化计算的0.536 MPa减少将近一半;且实际最大的井壁竖向拉应力并非出现在刃脚根部,而是刃脚根部以上2 m、隔墙底部变宽处,相应值为0.677 MPa。分析原因,由于在隔墙上部与井壁刚度相差不大,变形比较均匀;到了隔墙变宽处,井壁厚为2 m,隔墙厚1.4 m,两者刚度比值发生较大变化,即隔墙与井壁的框架作用突然减弱,因此出现较大变形,相应的应力也较大;而对于隔墙变宽处以下,隔墙厚度虽然逐渐减弱,但隔墙与井壁的框架作用并不明显,即在此处沉井井壁的水平面内变形小于其面外的变形。
4 结 论
(1)在沉井初始下沉时,井壁底部支撑沉井的地基刚度相对沉井较小,若按照弹性支承模拟,计算参数较难选取;根据计算分析,弹性支承的刚度对隔墙受力影响相对较小,设计时可以偏安全的假定井壁底部竖向固结来计算隔墙受力。
(2)沉井在首节预制时需进行地基加固,但如果加固强度过大对沉井受力并不是很有利;因此在施工时,满足基本承载力要求的前提下,可考虑适当降低安全系数,以节省施工费用。
(3)沉井下沉到位后,通过对平面计算和实体空间计算比较:平面计算假定较多,与实体分析有一定差别,计算偏于保守,特别采用刃脚根部以上的井壁平面计算结果作为井壁配筋的控制,浪费较大。因此,设计若采用平面简化计算,计算荷载仅需考虑该段井壁高度范围内相应的水土压力而不需要施加刃脚的水平力。
(4)通过实体分析,隔墙的刚度对井壁的受力有较大影响。在沉井下沉到位后,在水平土压力作用下,井壁最大的拉应力均出现在隔墙的刚度变化位置与井壁相交的地方。在结构设计时,需引起重视,加强对局部的检算。同时,隔墙的厚度变化尽量缓和,以避免由于隔墙刚度的突变引起井壁局部的应力集中。
[1] 周世忠. 江阴长江公路大桥北锚碇的施工与控制[J]. 国外桥梁, 2004,(4): 56-59.
[2] 吉 林, 冯兆祥, 周世忠. 江阴大桥北锚沉井基础变位过程实测研究[J]. 公路交通科技, 2001,18(3): 33-35.
[3] 黄龙华,周 炜,刘 涛.泰州长江公路大桥中塔墩沉井基础施工方案研究[J]. 桥梁建设,2008,(2):63-66.
[4] Guo Zheng-Hong ,Xu Wei. Research on the stress mechanism of the ultra-deep open caisson system during subsidence process[C]//Proceedings of the GeoShanghai Conference - Underground Construction and Ground Movement, Geotechnical Special Publication, 2006: 142-149.
[5] 李宗哲, 朱 婧, 居炎飞, 等. 大型沉井群的沉井下沉阻力监测技术[J]. 华中科技大学学报(城市科学版), 2009, 26(2): 43-46.
[6] Allenby D,Waley G, Kilburn D. Examples of open caisson sinking in Scotland[C]//Proceedings of the Institution of Civil Engineers: Geotechnical Engineering, 2009: 59-70.
[7] 苏静波, 楼淑君, 霍瑞丽. 锚碇沉井基础稳定性的规范算法与有限元方法的对比[J]. 盐城工学院学报(自然科学版), 2008, 21(4): 4-7.
[8] 李跃进. 厚砂层中的沉井施工方法[J]. 山西建筑, 2008, 34(6): 184-185.
[9] 苏静波, 楼淑君, 霍瑞丽. 锚碇沉井基础稳定性的规范算法与有限元方法的对比[J]. 盐城工学院学报(自然科学版), 2008, 21(4): 4-7.

