高精度恒星孔径测光注释
曾开华,彭青玉,3
(1.暨南大学计算机科学系, 广州 510632;2.广东省高等学校光电信息与传感器技术重点实验室, 广州 510632;3.中国科学院光学天文联合开放实验室, 昆明 650011)
天体测量通常关心的是星像的位置,而较少考虑星像的亮度。对于天然卫星的互掩互食观测,利用测光结果却能够准确地进行天体测量[1]。而这种测量的精度与天空背景关系密切[2]。所以希望通过深入探讨测光方法,提高测光精度,从而更好地进行天体测量。
目前,主流测光技术有孔径测光和点扩散函数测光两种。通过计算总通量的孔径测光方法适合孤立、较亮的星像观测。而点扩散函数方法则更多地用于测量密集、较暗的星团[3-4]。然而,即使是利用相对简单的孔径测光技术,要精确求解星像的亮度也是十分复杂的。本文选择孔径测光方法,并采用云南天文台1m望远镜的图像进行实验。在Stetson[5]和Da Costa[6]等人工作的基础上,对曝光量、天空背景、像素取舍、信噪比和生长曲线等相关问题进行讨论并总结实验所得的经验。
本文第1部分介绍了利用孔径测光方法得到恒星仪器星等的全过程。第2部分描述了所用的资料及实验结果。第3部分与测光软件IRAF作比较。第4部分结合实验结果对相关问题进行深入讨论。最后一部分是结论。
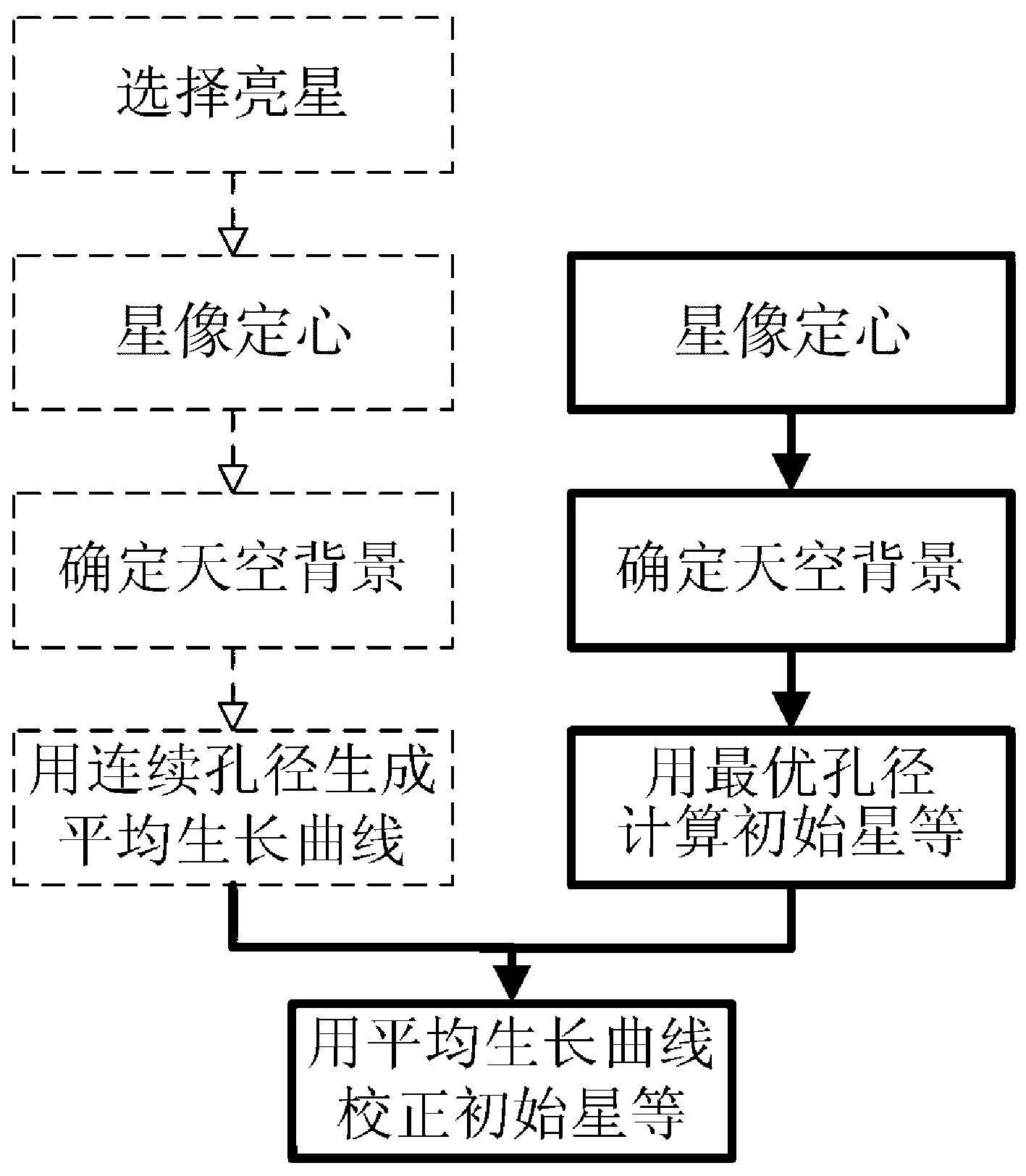
图1 孔径测光流程Fig.1 Flowchart of aperture photometry
1 孔径测光
为了测量CCD图像中星像的亮度,需要把所有星像的光加起来并转换为星等。由于求和通常在一个圆形区域内进行,所以该技术称为孔径测光[6]。孔径测光过程一般分为4个主要步骤:星像定心、确定天空背景、计算初始星等和孔径校正,整个流程如图1。
1.1 星像定心
星像中心的精确测定对于孔径测光来说是重要的,尤其是小孔径测光。经典的定心算法有:高斯拟合法、修正矩方法、中值法和寻导法等[7]。根据李展等人最新的研究结果[8],高斯拟合法具有较高的精度,所以选取它作为定心算法。
1.2 确定天空背景
确定天空背景一般通过分析星像周边圆环状对称区域内像素的灰度值来实现。圆环内应包含尽量多的像素,而且必须远离星像的中心(至少是几倍的FWHM)。实验中,圆环的外半径是内半径的2倍。
对天空背景中出现的不同灰度值进行统计,可得到天空背景的直方图。一般地,直方图呈现对称高斯函数的形状。对直方图进行一维高斯函数最小二乘拟合来求解中心。该中心是出现频率最高的灰度值,可作为天空背景的估计。本文称此方法为直方图法。
有时由于亮星边缘、暗星、星系和宇宙射线等的影响,直方图可能呈现一定程度的倾斜,而不再对称。参考文[6],此时天空背景的均值、中值和众数并不相同,其中均值受影响最大,中值其次,众数最轻。因此,众数是对天空背景的最好估计,可以通过下式给出[9]:
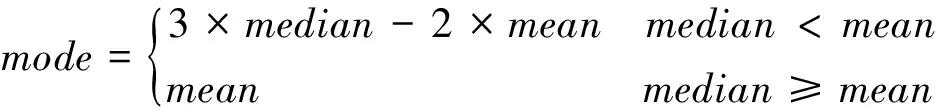
(1)
通过不断迭代计算,剔除那些偏离中值2.5~3倍标准差的像素点,最终可以得到稳定的众数。通常,人们称此方法为“3-2”公式法。
1.3 计算初始星等
星像的亮度通常用星等(m)来表示:
m=zpt-2.5logI
(2)
其中zpt就是星等的零点,可以取25或23.5。而通量I为:
I=∑(Ii,j-isky)
(3)
Ii,j是孔径中像素点(xi,yj)的灰度值;isky是天空背景。
对于孔径的大小,当然选择足够大的孔径,使得它能包含星像所有的光。这样的孔径至少是4~5倍的半峰全宽(FWHM),实验中取5倍FWHM,称为最大孔径。对于亮星,最大孔径能包含几乎所有的光;但对于暗星,则把天空背景的噪声也包含在其中,影响了测量精度。
实际上,常采用信噪比最大时的孔径作为测量的孔径,称为最优孔径。信噪比[10-12]由下式给出:
(4)
其中N*是孔径内星像光的总记数值;npix是孔径内像素的数目;Ns为天空背景;Nd为每一像素的暗流;而Nr则为CCD的读出噪声。对于现在大部分用于天文研究的CCD系统,暗流Nd可以忽略不计[10]。
1.4 孔径校正
最优孔径的选择自然会引出孔径校正的概念。由于星像的最大信噪比通常在较小的孔径就能达到(约0.68倍FWHM),而小孔径并没有包括星像所有的光(约72%)[4,13],丢失的部分需要通过校正来补偿。把从最优孔径到最大孔径的校正过程称为孔径校正。
用一系列逐渐增大的同心孔径来测量星像,然后计算连续孔径之间的星等差,也就是用大孔径测得的星等减去小孔径测得的星等。这些星等差是关于孔径半径的函数,随着孔径的增大形成一条逐渐递增,近似对数函数的离散曲线,称为生长曲线。由于亮星的信噪比好,星等测量精度高,其生长曲线较平滑,所以利用亮星的生长曲线来做孔径校正(图1)。把最大孔径到最优孔径之间丢失的光对应的星等差补偿到最优孔径测得的初始星等上,从而使得最优孔径也能达到最大孔径测量的效果。
2 观测资料及实验结果
对云南天文台1m望远镜观测星团NGC1664和星团NGC2168的CCD图像进行资料分析。望远镜和CCD的有关参数见表1,资料集的说明见表2。

表1 望远镜和CCD的参数说明Table 1 Specifications of the telescope and CCD chip

表2 资料集说明(其中滤光片为Johnson I)Table 2 Specifications of the image sets (filter: Johnson I)

图2 典型NGC1664的CCD图像Fig.2 Typical CCD image of NGC1664
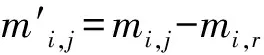
在Windows环境下,使用C#程序语言开发了自己的测光程序。目前,在宁静度条件较好的情况下(FWHM=1.3~1.9 arcsec,由Gauss轮廓拟合获得),测得亮星(约10~12mag, 取自星表USNO-B1.0[14])的内部精度通常可以达到0.003mag,而暗星(约17mag)大约在0.2mag(见图4中的黑色圆点)。


图4 用生长曲线方法与IRAF测量内部精度的比较:(a)使用资料集1;(b)使用资料集2;(c)使用资料集3;(d)使用资料集4Fig.4 Comparison of internal precisions with the curve-of-grawth method and ZRAF: (a) image set 1; (b) image set 2; (c) image set 3; (d) image set 4
3 与IRAF比较
实验的同时,用自己的程序与测光软件IRAF[15]进行比较。IRAF中的APPHOT[16]是针对中等拥挤或稀疏星场进行孔径测光的软件包。在熟悉使用IRAF和APPHOT包的情况下,用生长曲线方法与APPHOT进行内部精度的比较。如图4,对于亮星,生长曲线方法的测量内部精度和APPHOT相当。对于中等亮度的星和暗星,生长曲线方法则稍优于APPHOT。
4 讨 论
4.1 曝光量
影响恒星测光精度的主要因素首先是星像的曝光量,其次是天空背景的估计和测量孔径等。上文对亮星测量的内部精度可以达到0.003mag,而暗星却只有0.2mag,其主要原因在于暗星的曝光量不足。换言之,对暗星如果增加曝光时间,可以显著提高其测光精度。但这有一定的限度,主要的限制来源于天空背景的影响。因为延长曝光时间,在增加暗星曝光量的同时,天空背景值也相应地增加。本文所使用的图像曝光时间为60s或100s是合适的。它使得亮星不至于饱和,而暗星也刚好能观测到。
4.2 天空背景
天空背景的估计是影响测光精度的另一主要因素[8,17],尤其是暗星的测量。实验中发现直方图法和“3-2”公式法都比较准确。无论背景是均匀或是倾斜的,甚至旁边有伴星的情况下,都能得到令人满意的结果。而有的时候,“3-2”公式法求得的结果会高出直方图法约0.1~0.2个计数值。
4.3 像素取舍
因为参与计算通量的像素点可能只有少数的几个或几十个,孔径内任何一个像素的采纳或舍弃都对星等产生影响,尤其是小孔径测量。对此,在程序中采用了Stetson的线性加权方法[18]。
4.4 信噪比
采用信噪比最大时的孔径作为测量的最优孔径,使得孔径中的像素不至于太少,也不会由于孔径太大而引入天空背景的噪声。它最优地抽取有用数据,在一定程度上减少测量中天空背景误差对星等精度的影响。不同亮度的星像,达到最大信噪比的半径通常不同(大约在0.68倍FWHM[4,13])。图5是视星等分别为14.8、15.7和17.0的3颗星在不同孔径中信噪比的变化情况。而图6则是这3颗星在对应的孔径中星等测量的内部精度。可以看出,信噪比的变化对暗星测量精度的影响远远大于亮星。而在信噪比达到最大时,星像的测量精度一般是最好的。

图5 3颗不同亮度的星信噪比随孔径的变化情况Fig.5 SNR values of three stars of different apparent magnitndes in different apertures
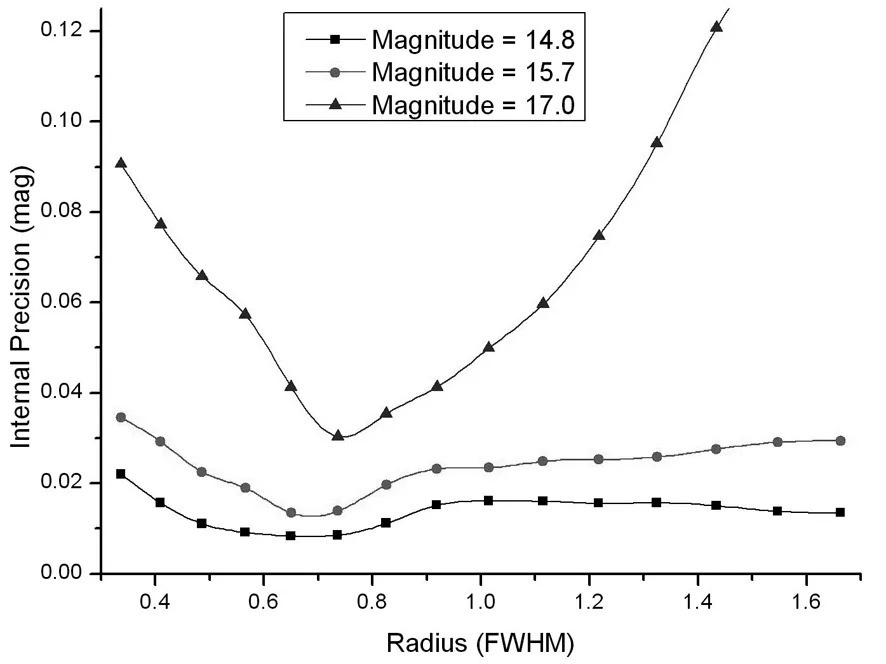
图6 3颗不同亮度的星测量精度随孔径的变化情况Fig.6 Internal precisions of three sturs of different apparent magnitudes in different apertures
4.5 生长曲线
在没有受到望远镜光学系统可能的像差影响的线性CCD图像中,每一颗星的点扩散函数都认为是一样的,不同的只是通量和位置。也就是说,亮星和暗星只存在着一个关于通量比例系数的差别。它们在同样大小的孔径中,分得星像的光占总光量的比例是一样的[5-6,19]。

其中ml和ms分别是连续孔径中较大和较小的孔径测得的星等,Il和Is是对应的通量。可以看出同一个星像在不同孔径的星等差其实是关于自身通量比例的函数。因此,亮星和暗星应该遵循同样的生长曲线。图7是同一视场中视星等分别为9.1、12.5和16.1的3颗星的生长曲线。其中两颗中等偏亮的星能一致地吻合于同一生长曲线,称为平均生长曲线。星等为16.1的暗星在靠近中心的部分能较好地吻合平均生长曲线,但远离中心的部分受到天空背景噪声的影响,而呈现上下波动的情况。这正是需要使用最优孔径计算初始星等,用生长曲线技术校正的原因。
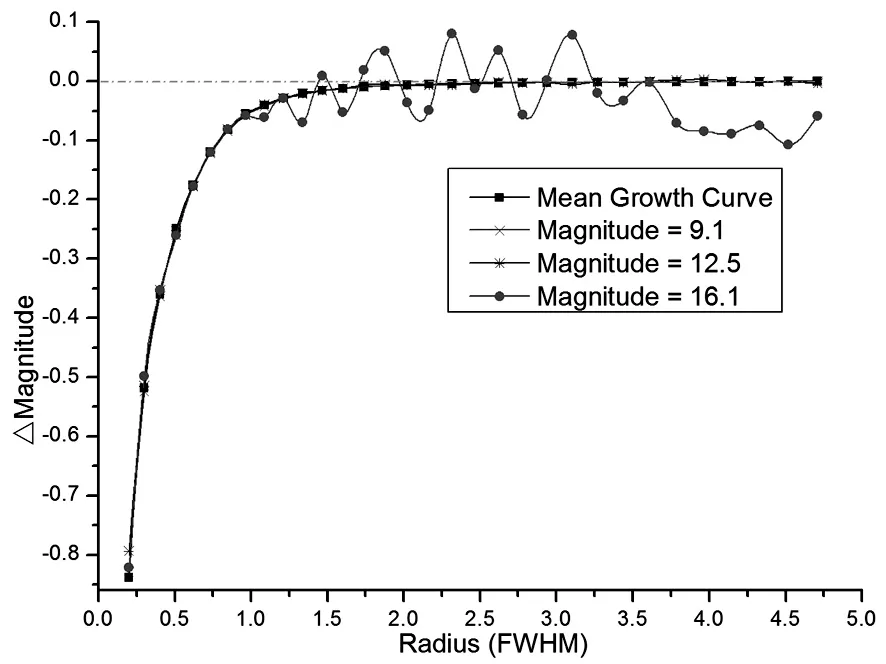
图7 3颗不同亮度的星的生长曲线Fig.7 curves-of-grawth of three sturs of different apparent magnitades

图8 不同宁静度下的平均生长曲线Fig.8 Averaged curves-of-growth at different seeings
影响星等测量精度的另一个因素是平均生长曲线能否准确反映真实情况,即图像中不同位置不同亮度的星像是否都遵循同一条平均生长曲线。实验中,由于视场非常小(约7′×7′),为了简便,对整幅图像只采用一条平均生长曲线。但在实际中,一幅图像不同区域的宁静度可能具有一定的差异,特别是大视场观测的时候。而宁静度的不同使得同一大小的孔径中分得星像光量的比例不一致,导致星像可能并不吻合于同一生长曲线。图8 展示了宁静度为1.2、1.4和1.6 arcsec 3种条件下,同一视场的平均生长曲线。可见,不同宁静度下平均生长曲线是差别较大的。应该根据具体情况,把一幅图像划分为若干宁静度近似相同的区域,不同区域中使用不同的平均生长曲线来校正。
因为亮星的信噪比高,应该选取亮星作为生成平均生长曲线的星像。但并不适合选择最亮的星像,因为这类星像容易饱和,而且覆盖范围太大,甚至出现光晕。同时,选取的亮星应该尽量孤立且周边没有受到伴星或不良像素的影响。
4.6 其他方面的影响
测光精度与平场、Bias和暗流(长时间曝光时)也有一定的关系,尤其是平场[20-21]。本文在实验之前已经使用IRAF对所有图像进行了相应的处理,并在这样相同的平场处理条件下进行精度比较的。
5 结 论
高精度孔径测光通常要认真考究天空背景、像素取舍、最优孔径及孔径校正等因素。通过使用自己开发的程序,对云南天文台1m望远镜观测的CCD图像进行实际测量,并与测光软件IRAF进行比较。结果表明:亮星(约10mag)的内部测量精度能达到0.003mag,而暗星(约17mag)达到0.2mag。对于中等亮度的星和暗星,最优孔径和生长曲线的技术能较好地提高测量精度,在测量的内部精度方面稍优于IRAF。
致谢:感谢暨南大学计算机科学系张庆丰老师、孟小华老师、李展老师为本文提出了建设性建议。
[1] Arlot J E, Thuillot W, Ruatti C, et al.The PHEMU03 catalogue of observations of the mutual phenomena of the Galilean satellites of Jupiter[J].A&A, 2009, 493: 1171-1182.
[2] Emelyanov N V.Mutual occultations and eclipses of the Galilean satellites of Jupiter in 2002-2003: final astrometric results[J].MNRAS, 2009, 394: 1037-1044.
[3] Handler G.Combining Aperture and PSF-Fitting Photometry [J].BaltA, 2003, 12: 243-246.
[4] Mighell K J.Algorithms for CCD Stellar Photometry[J].ASPC, 1999, 172: 317-328.
[5] Stetson P B.On the growth-curve method for calibrating stellar photometry with CCDs [J].PASP, 1990, 102: 932-948.
[6] Da Costa G S.Basic Photometry Techniques[J].ASPC, 1992, 23: 90-104.
[7] Stone R C.A comparison of digital centering algorithms[J].AJ, 1989, 27: 1227-1237.
[8] 李展, 彭青玉, 韩国强.CCD图像数字定心算法的比较[J].天文学报, 2009, 50(3): 340-348.
LI Zhan,PENG Qing-yu,HAN Guo-qiang.Comparison of Digital Centering Algorithms Based on CCD Images[J].Acta Astronomica Sinica,2009,50(3):340-348.
[9] Kendall M, Stuart K.The Advanced Theory of Statistics[M].London: Charles Griffin & Co., 1977.
[10] Howell S B.Two-dimensional aperture photometry-Signal-to-noise ratio of point-source observations and optimal data-extraction techniques[J].PASP, 1989, 101: 616-622.
[11] Howell S B.Introduction to Time-Series Photometry using Charge-Coupled Devices[J].JAVSO,1991, 20: 134-149.
[12] Herbert R.Detecting and measuring faint point sources with a CCD [EB/OL].http://www.pdfmailer.com.
[13] Mighell K J.CCD Aperture Photometry[J].ASPC, 1999, 189: 50-55.
[14] Monet D G, USNO-B Team.The USNO-B1.0 Catalog [J].AAS, 2002, 34: 1104.
[15] Tody, Doug.The IRAF Data Reduction and Analysis System [J].SPIE, 1986, 627:733.
[16] Lindsey E D.A User’s Guide to the IRAF Apphot Package[EB/OL].http://iraf.noao.edu.
[17] Bridzius A, Vansevicius V.The Aperture Photometry: a Software Package for IBM Personal Computers[J].BaltA, 1997, 6: 661-676.
[18] Stetson P B.DAOPHOTO: A computer program for Crowded-Field stellar photometry [J].PASP, 1987, 99: 191-222.
[19] Anderson J, Bedin L R, Piotto G, et al.Ground-based CCD astrometry with wide field imagers. I.Observations just a few years apart allow decontamination of field objects from members in two globular clusters[J].A&A, 2006, 454: 1029-1045.
[20] Peng Q Y, Tan Pei An.Effect of CCD photometric calibration on precise measurement of stellar image[J].Astronomical Research & Technology, 2005, 2(1): 28-33.
[21] 刘新德, 张云, 卢汝为, 等.CCD平场改正精度对CCD测光精度的影响[J].云南天文台台刊, 1988, 1: 72-76.
Liu Xinde,Zhang Yun,Lu Ruwei,et al.Effects of the Correction Accuracy of the CCD Flat Field on the CCD Photmetril Acuracy[J].Publications of Yunnan Observatory,1988,1:72-76.

