兴隆1m光学望远镜杂散光效应研究

赵 飞，王 森

(1.中国科学院国家天文台，北京 100012;2.中国科学院研究生院，北京 100049;3.中国科学院光学天文重点实验室(国家天文台)，北京 100012)

国家天文台兴隆1m光学望远镜是具有耐史密斯(Nasmyth)焦点的R-C系统。望远镜有效通光口径φ1000mm,系统焦距8226mm，在ω=0.21°优化视场内, 80%能量集中在1″。望远镜采用1340×1300像元液氮制冷CCD(参数见表3)，CCD感光面对应物方视场13.2′×12.8′。该望远镜采用桁架结构，安装了副镜遮光罩和第三反射镜(平面镜)遮光罩以抑制杂散光[1]。

图1 兴隆1m光学望远镜光路示意图[1]Fig.1 Optical layout of the Xinglong1-meter optical telescope

该望远镜在大月夜对邻近月天区望远镜指向与月方位间夹角为5°≤ |θ| ≤ 30°范围的天体进行观测时，观测到图像的背景噪声明显增大，并且不均匀。这些现象说明，在大月夜观测条件下，该望远镜存在明显的杂散光效应，直接影响了观测信噪比。为降低月亮导致的杂散光对天文观测的影响，特别是提高天体测光观测性能，已经在望远镜桁架上加装了系列挡板，用涂黑蒙皮覆盖特定结构的表面。这些都是基于经验和定性分析而设计的措施，在本文中称为 “定性措施”。

在本文的研究工作中，首先利用Tracepro软件，对在圆顶-1m光学望远镜组合系统的杂散光传播路径进行了定量计算和分析。基于对望远镜杂散光的计算分析结果，提出了针对该望远镜的进一步抑制杂散光的改进措施，在本文中称为“定量措施”。分别对望远镜采用“定性措施”和“定量措施”前后的 “归一化点源辐照度透过率(PSNIT)”进行计算，并以PSNIT为评价函数，对“定性措施”和“定量措施”对该望远镜杂散光的抑制效果进行评价和讨论。此外，本文还计算了该望远镜采用挡板、叶片等不同措施时有效视场外无限远点源为杂散光源所产生的杂散光辐照度在焦面的分布情况，定量计算了圆顶天窗开口宽度、望远镜指向高度角、副镜位置等结构参数的变化对其PSNIT的影响。最后，计算分析了采取不同杂散光抑制措施时,考虑满月杂散光环境的该望远镜的观测信噪比(SNR)、测光精度、灵敏度和望远镜观测极限星等。

1 兴隆1m光学望远镜杂散光抑制措施

兴隆1m光学望远镜已经采用的基于定性分析的杂散光抑制措施(“定性措施”)包括:(1) 如图 2(1)，在桁架上沿望远镜光轴方向加装8片通光口径φ1030mm、间隔120mm相互平行的挡光板，且所有挡光板表面涂黑;(2)望远镜桁架结构表面用涂黑的蒙皮包裹;(3)圆顶天窗开口侧壁用涂黑的蒙皮覆盖，其表面涂黑工艺的光传播特性参数列于表2中。

圆顶内该望远镜的杂散光传播路径计算结果(见第3.1节)表明：视场外临域任意方位无限远点源所产生的杂散光中，仅通过望远镜自身结构而未通过圆顶传播到达望远镜焦面的杂散光占到了75%以上。因此，对该望远镜杂散光抑制措施的设计应重点考虑对望远镜自身结构中杂散光传播“关键物”的优化。本文采用“反向光线追迹方法[2]”确定了该望远镜自身结构中杂散光传播的关键物(图 2)，提出了1m光学望远镜杂散光抑制“定量措施”方案,具体内容包括：

关键物(1)：主镜孔径光阑面上部。杂散光抑制措施如图2(2),在光阑上表面4个角各安置14片相互平行且垂直于光阑上侧表面的条形叶片阵列。叶片高度为50mm，间隔10mm，表面涂黑。

关键物(2)：第3反射镜与望远镜F/8焦面之间圆筒的内壁。杂散光抑制措施如图2(3),在与F/8焦面距离分别为177mm、432mm和826mm的位置设计了3个杂散光光阑。光阑表面采用发黑工艺处理。

关键物(3)：第3反射镜圆筒形遮光罩的内、外壁。杂散光抑制措施如图2(4),①从遮光罩上端开始，在遮光罩内侧沿其轴向安置10个相互平行且与圆筒璧同心的圆环形叶片，圆环内直径φ210mm, 间隔10mm，表面涂黑。②将发黑处理的遮光罩外壁涂黑以增大遮光罩外表面吸收率。

关键物(4)：副镜遮光罩内壁。杂散光抑制措施如图2(5),在遮光罩内侧安置4个与其侧壁同心的圆筒形叶片阵列，直径分别为φ304mm、φ318mm、φ332mm、φ294mm，叶片底与副镜遮光罩底沿光轴方向距离分别为12mm、24mm、36mm、48mm，叶片表面涂黑。

以上全部杂散光抑制措施中所采用涂黑和发黑工艺的光传播特性参数列于表2中。

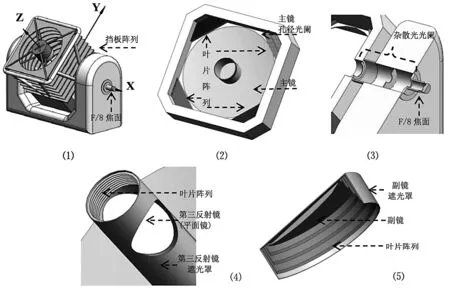
图2 兴隆1m光学望远镜“定性措施”和“定量措施”示意图Fig.2 Qualitative and quantitative stray-light controlling measures for the 1-meter optical telescope

图2(1) 望远镜桁架上的系列中心通光涂黑挡光板及“望远镜指向坐标系”示意图。(望远镜指向坐标系以第3镜几何中心为原点，其Z轴正向为望远镜指向，X轴正向为望远镜高度轴的F/8焦面方向。)；(2)主镜孔径光阑上表面4个角处的平行叶片阵列；(3)在第3反射镜与F/8焦面之间圆筒内壁安置3个消杂散光光阑(剖视图)；(4) 在第3反射镜圆筒形遮光罩内壁安置的圆环形叶片阵列；(5)在副镜遮光罩内壁安置的4个的圆筒形叶片阵列(剖视图)。

2 兴隆1m光学望远镜杂散光抑制措施的定量评价

2.1 兴隆1m光学望远镜杂散光分析计算模型

图3是“圆顶-1m光学望远镜”组合系统在Tracepro软件中建立的计算模型。望远镜和圆顶结构是基于设计文件建立在模型中的，模型中也包括了第1节中所述的“定性措施”和“定量措施”。 模型中圆顶天窗开口的宽度取最大值2m，望远镜指向高度角设定为45°。

图 3 兴隆1m光学望远镜杂散光计算模型左图：“圆顶-1m光学望远镜”组合系统模型图 右图：全部“定性措施”和“定量措施”模型图

工况组合系统所采用的杂散光抑制措工况1系统未采用定性措施和定量措施工况2系统仅采用定性措施工况3系统同时采用定性措施和定量措施工况4在工况3基础上，系统全部“涂黑”面更换成“增强型高吸收率涂层面(EMB)”

2.2 杂散光定量评价函数的选取

兴隆1m光学望远镜采用桁架结构并置于圆顶内使用，难以明确定义其杂散光能量进入的有效孔径。因此，本文选取独立于杂散光进入孔径的“归一化点源辐照度透过率(Point Source Normalized Irradiance Transmittance，简称PSNIT)”，作为望远镜杂散光效应评价函数。如式(1),PSNIT定义为：来自有效视场外无限远点源的杂散光到达望远镜焦面上的辐照度与望远镜入瞳面上该点源辐照度的比值[3]。PSNIT是视场外无限远点源方位与望远镜指向之间夹角θ的函数，同时可以看到杂散光在望远镜成像焦面的分布并不均匀，焦面上不同位置对应不同的杂散光辐照度，因此PSNIT也是焦面位置坐标x、y的函数。在计算本望远镜焦面上的杂散光辐照度时，把单位面积归化到所用CCD像元的面积。如式(2),本文采用全焦面杂散光辐照度的平均值计算PSNIT。同时，全焦面杂散光辐照度平均值也是焦面上杂散光总能量的表征[3]。

(1)

(2)

E(x,y)focal plane_straylight系统焦面上不同位置处来自视场外无限远杂散光点源的辐照度;Epointsourc_straylight为望远镜入瞳面上该点源辐照度。

2.3 PSNIT的计算方法和参数

在1m望远镜杂散光计算模型中设置有效视场外无限远点源为杂散光源，采用蒙特卡罗光线追迹方法[4]计算焦面上杂散光辐照度的平均值和相应的PSNIT。圆顶、望远镜和杂散光抑制措施中各部件的光能量传播参数列于表2中。对于结构表面的散射特性，采用BRDF(Bidirectional reflectance distribution function)函数描述, 其定义为：在光散射方向上，被散射光的辐亮度与散射面所接收辐照度的比值[4]。本文采用的是ABg形式的BRDF函数,其中A,B,g是确定BRDF函数的3个参数[5]。

表2 兴隆1m光学望远镜杂散光计算模型中光能量的传播参数列表 (适用波段λ=550～900nm)( EMB：增强型高吸收率涂层)Table 2 Parameters for light transimission in the calculation model of the stray light for the Xinglong 1-meter optical telescope(Applicable wavelength range:λ=550～900nm; EMB:Electrostatic Magnetic Brush coationg)

2.4 定性措施和定量措施对望远镜杂散光抑制效果的分析和评价

分别计算了上述4种工况下“圆顶-1m光学望远镜”组合系统的PSNIT值。计算所设置的无限远杂散光点源位于望远镜指向坐标系O-X-Z平面内，其方位与望远镜指向间夹角范围取5°≤|θ|≤ 60°(Z轴方向对应夹角θ=0°，X轴方向对应夹角θ=+90°)。

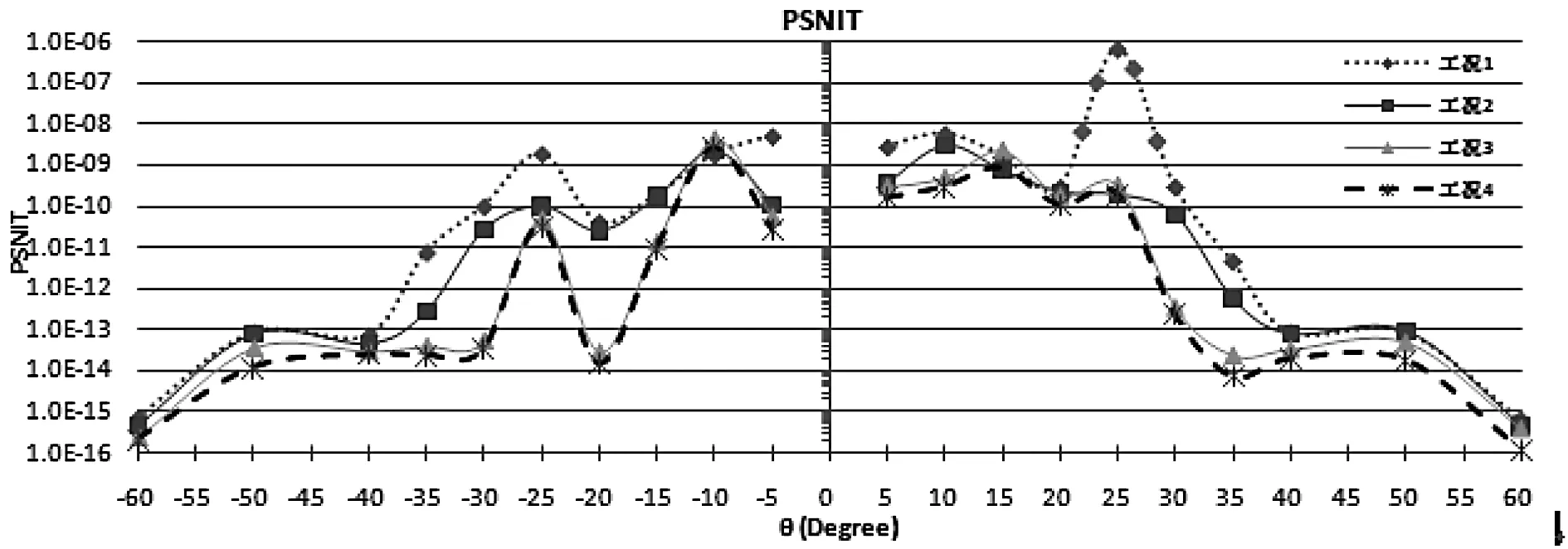
图 4 兴隆1m光学望远镜四种工况下的PSNIT计算结果Fig.4 PSNIT calculation results for the Xinglong 1-meter optical telescope with different stray-light controlling measures

对图4结果进行分析可以看出：

(1)工况1系统未采用“定性措施”和“定量措施”时，其PSNIT在 5°≤|θ|≤30°范围内全部高于10-10，最大值出现在θ=+25°，达到10-6；

(2)工况1和工况2两组曲线的对比说明，仅采用 “定性措施”后系统的PSNIT值在5°≤|θ|≤60°范围内可以降低到10-8以下，但在5°≤|θ|≤30°范围仍高于10-10，PSNIT的优化幅度小于2个数量级；

(3)工况2和工况3两组曲线的对比说明，“定性措施”和“定量措施”同时使用，系统的PSNIT值在5°≤|θ|≤60°范围内的多个方位可以得到进一步的优化，在5°≤|θ|≤30°范围内部分方位PSNIT降到10-10以下，多个方位优化幅度达3个数量级，特别是在θ=25°时，PSNIT得到约为4个数量级的最大降幅；

(4)计算工况4下系统PSNIT的结果可以评价“优化表面涂层方法”对该系统杂散光效应的优化效果。可以看出，在工况3的基础上进一步采取这一措施后，系统PSNIT在5°≤|θ|≤60°范围内降低幅度局限于1个数量级之内，与系统采用的“定性措施”加“定量措施”相比，表面涂层优化方法对该系统杂散光效应的优化效果不明显。

3 兴隆1m光学望远镜杂散光效应分析

3.1 杂散光传播途径的分析

当“圆顶-1m光学望远镜”组合系统处于工况2时，其杂散光传播途径可分为3类：通过圆顶内壁散射传播；通过圆顶天窗开口侧壁散射传播；仅通过望远镜自身结构传播。为研究通过上述3类路径传播的杂散光效应，本节利用第2节中所建立的计算模型，对各类杂散光传播途径分别单独作用和3类途径同时发生作用的情况分别进行了计算。图5中的A、B、C曲线表明了有效视场外无限远点源(5°≤|θ|≤60°)所产生的杂散光中，分别通过上述3类路径到达系统焦面的杂散光能量与通过3类途径共同到达焦面的杂散光能量之比。通过计算结果可以看出，仅通过望远镜自身结构传播的杂散光能量占75%以上。因此，该望远镜杂散光抑制措施的设计应着重于对望远镜自身结构的优化。

图 5 通过不同路径传播的杂散光能量比例Fig.5 Ratios of stray-light powers transmitted through different paths

3.2 杂散光抑制措施对焦面杂散光分布均匀度的影响

在影响天文“较差测光(differential photometry)”精度的诸多因素中，观测天体背景强度不均匀是个重要的误差来源。焦面杂散光的分布越不均匀，较差测光的误差就会越大[10]。因此，有必要对各工况下望远镜焦面杂散光分布的均匀程度进行统计,以分析抑制措施对焦面杂散光分布的影响。本文采用如式(3)所示的全焦面杂散光辐照度数值的标准差为评价函数。焦面杂散光辐照度标准差越小意味着其分布越均匀。

Uniformity of stray light=Standard deviation[E(x,y)focal plane_straylight]

(3)[2,10]

图6列出了第2节中的前3种工况下有效视场外(5°≤|θ|≤60°范围内)无限远点源产生的全焦面杂散光辐照度的标准差。由于工况4对应数据与工况3较接近，这里对工况4不另做分析。图中数据显示各θ所对应标准差随工况的改变趋势并不一致，且没有明确的分布规律。这一计算结果说明：1m光学望远镜采取“定性措施”和“定量措施”后，焦面杂散光分布的均匀程度未能得到有效的改善。

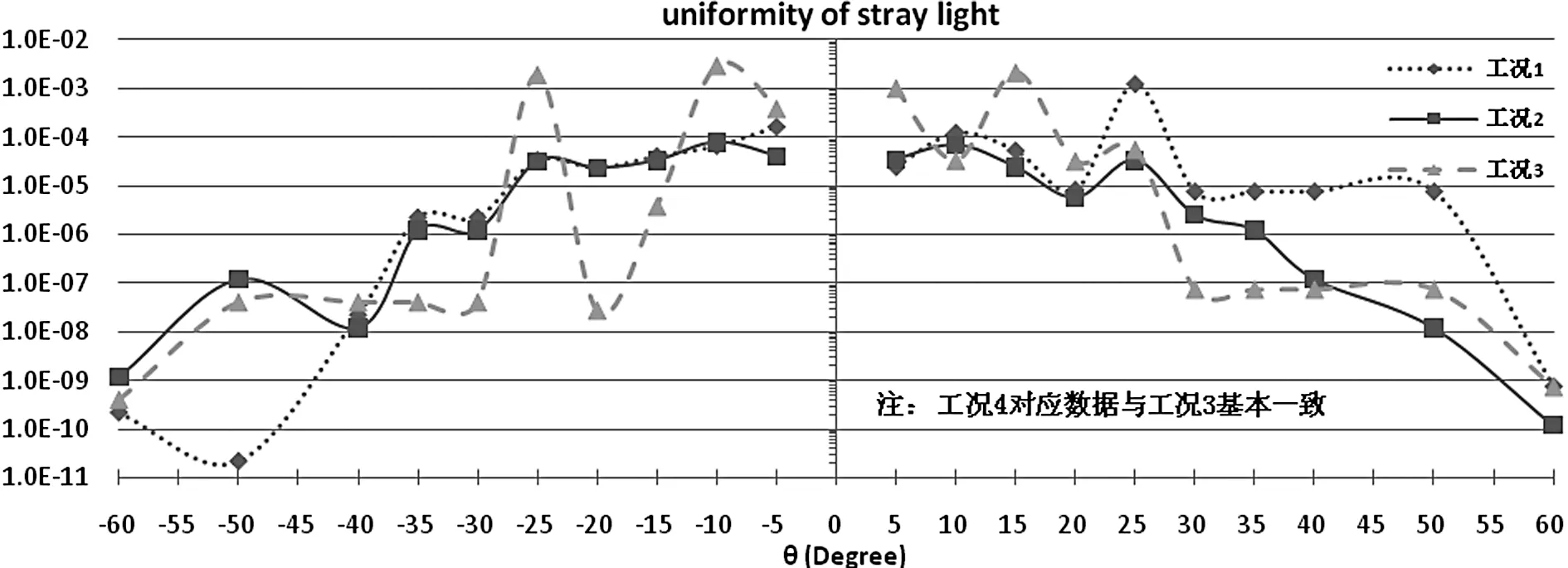
图6 各工况下有效视场外无限远点源产生的焦面杂散光辐照度标准差计算结果Fig.6 Calculated variations in stray-light irradiance on the focal plane in each working status (assumed to be from point sources at infinity and out of the effective field of view)

3.3 结构参数变化对PSNIT的影响

根据观测需求，在天文观测过程中望远镜圆顶天窗开口的宽度、指向高度角、副镜位置等都会变化，这些在杂散光效应分析中都归为结构参数的变化。本节采用第2节中所建立模型，计算了上述3项结构参数变化对工况2条件下 “圆顶-1m光学望远镜”系统PSNIT的影响。不同圆顶天窗开口宽度对应的PSNIT数值列于图 7中。数据结果显示，圆顶天窗开口越小，系统的PSNIT越低。在20°≤|θ|≤30°范围内，减小天窗开口宽度能够使得PSNIT降低约1个数量级。当无限远杂散光源处于上述区域时，减小圆顶天窗开口的方法可使1m光学望远镜杂散光效应得到一定优化。

图7 不同圆顶天窗开口宽度时1m光学望远镜的PSNIT计算结果(工况2)Fig.7 Calculated PSNIT values of the 1-meter optical telescope with different dome slit-aperture widths(under the working status 2)

1m光学望远镜另外两项结构参数是副镜可调焦沿轴移动±15mm，测光观测要求望远镜指向高度角不小于20°。PSNIT计算结果表明各工况下副镜位置调整和望远镜指向高度角变化对该望远镜PSNIT的改变小于3.5%。

4 兴隆1m光学望远镜杂散光效应对天文测光观测的影响

望远镜观测信噪比SNR是影响天文观测性能的重要指标[11]，进入望远镜焦面的杂散光将产生相应的背景噪声，导致观测SNR降低，进而影响对天体测光观测的精度、灵敏度和望远镜的观测极限星等。本节给出了考虑杂散光效应的望远镜观测SNR计算公式，结合兴隆站观测环境并以Johnson UBVRI测光系统[12]中的R波段15等星为例，模拟计算了兴隆1m光学望远镜在前述不同工况下考虑满月杂散光效应的望远镜观测SNR、测光精度和系统的探测极限星等，以此从观测性能评估望远镜杂散光抑制措施的有效性。

4.1 考虑杂散光效应的望远镜观测SNR计算方法

采用CCD的天文光学望远镜的观测SNR涉及的随机噪声主要包括散粒噪声、观测背景噪声和CCD系统的读出噪声。标准的望远镜观测SNR计算如式(4)所示[11]。当望远镜存在杂散光效应时，观测背景噪声由天光背景噪声和杂散光源产生的背景噪声两部分组成，并且两类噪声的来源相互独立。所以，考虑杂散光效应计算望远镜观测SNR时，式(4)中的Rback是天光背景和杂散光背景在单个CCD像元上产生光电子的速率之和，即Rback=Rback(天光)+Rback(杂散光)。式(5)是与望远镜观测SNR相对应的测光误差计算公式[11](以误差星等δm为单位)。

(4)

(5)

Rstar为被测星在CCD上产生光电子数的总速率(e-/second);Rback为观测背景在单个CCD像元上产生光电子的速率(e-/second/pixel);RN为读出噪声(e-)；G为CCD反向增益(e-/ADU);D为CCD暗流(e-/pixel/second);npix为 CCD输出图像上星像PSF内包含的像元数；t为积分时间(seconds)。

1m光学望远镜大月夜测光观测要求望远镜指向与月亮在天球坐标中的方位间夹角不小于15°。从前面的分析结果可知，未采用杂散光抑制措施时(工况1)，望远镜PSNIT最大值出现在θ= +25°及邻域。因此，本文在观测SNR计算中选择望远镜指向与满月方位间夹角θ=+15°和+25°这两个有代表性的方位进行计算。表2列出了兴隆站满月夜典型观测环境[13]、望远镜观测SNR计算所用参数及参数的前提条件、数据来源。其中工况2对应Rback(杂散光)=Rback(工况2)-Rback(天光)(工况2)。工况1和工况3对应Rback(杂散光)，是通过第2.3节中工况间PSNIT的比值等比例计算获得，具体计算方法在表3中用式(6)表示。

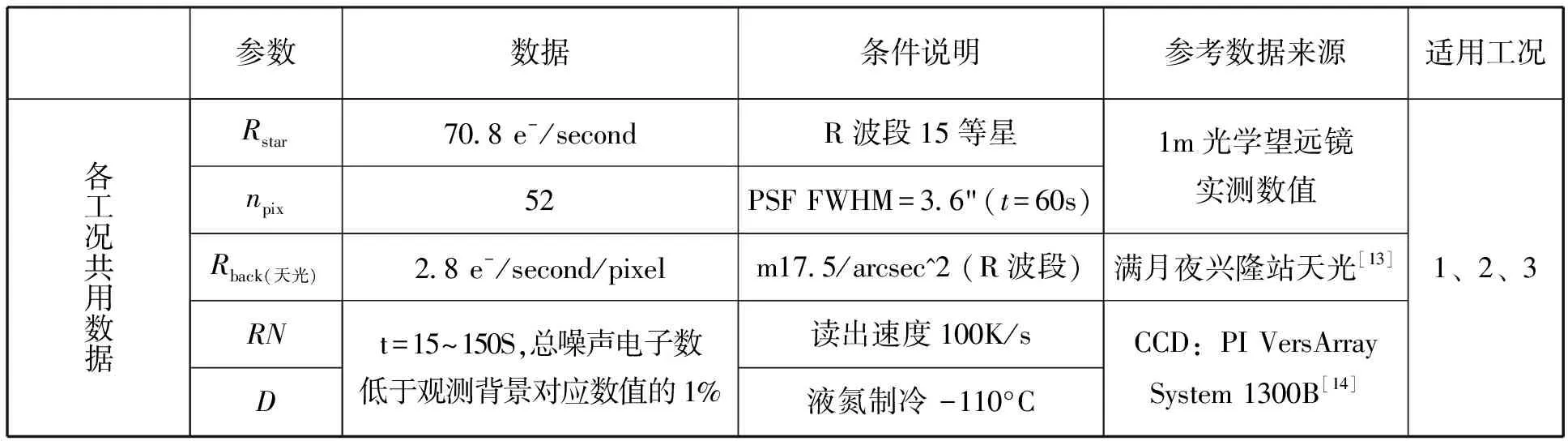
表3 兴隆1m光学望远镜观测SNR计算用参数列表Table 3 List of parameters for calculating SNR values in observations with the Xinglong 1-meter optical telescope

续表

参数数据条件说明参考数据来源适用工况各工况Rback(杂散光)计算方法和数据Rback68e-/second/pixelθ=+15°118e-/second/pixelθ=+25°1m光学望远镜实测数值Rback(杂散光)Rback-Rback(天光)满月杂散光对应数值2Rback(杂散光)Rback(杂散光)(特定工况)=Rback(杂散光)(工况2)×PSNIT(θ)特定工况/PSNIT(θ)(工况2) (6)1、3

4.2 杂散光抑制措施对观测SNR、测光精度和探测极限星等的影响

图 8列出了兴隆站满月夜观测环境下，θ=+15°和+25°，曝光时间t=15～150s，各工况下该望远镜观测R波段15等星的观测SNR模拟计算结果，表 4中列出了各工况下系统探测极限星等的计算结果和相应前提条件。

图8 兴隆1m光学望远镜满月夜R波段15等星观测SNR曲线Fig.8 Variation of SNR values with exposure times of the 1-meter optical telescope (for the observation of a 15 mag star through the R band in a nithg of full moon)

从图 8中数据可以看出，模拟计算该望远镜对R波段15等星的观测，在曝光时间15～150s范围：

(1)在θ=15°，工况2(望远镜仅采用“定性措施”)下望远镜观测SNR可提高约5%，测光误差可相应降低约2‰个星等；

(2)在θ=25°，工况2下望远镜观测SNR可提高约136%，测光误差可相应的降低约10‰个星等；

(3) 组合使用“定性措施”和“定量措施”(工况3)后，该望远镜这两个方位观测信噪比又可提升约20%。

5 结 论

本文针对兴隆1m光学望远镜的杂散光效应进行了系统的分析计算，主要数据结果和结论如下：

(1)该望远镜杂散光传播路径计算表明：在有效视场外5°≤|θ|≤60°范围，任意方位的无限远点源所产生的杂散光中，仅通过望远镜自身结构而未通过圆顶传播路径到达望远镜焦面的杂散光能量占约75%以上。该望远镜杂散光效应优化措施的重点是望远镜自身结构中杂散光传播“关键物”的优化。

(2)该望远镜杂散光定量计算结果表明：采用基于定性分析的杂散光抑制措施(“定性措施”)后，在杂散光源位于5°≤|θ|≤60°范围内，其PSNIT全部降低到10-8以下，降低幅度约2个数量级；进一步采用基于定量分析的杂散光抑制措施(“定量措施”)后，在杂散光源位于5°≤|θ|≤30°范围内，其PSNIT最大降幅达3个数量级；表面涂层优化方法对该望远镜PSNIT的优化幅度局限于1个数量级之内。

(3)该望远镜的杂散光效应分析表明：“定性措施”和“定量措施”的采用，未能使望远镜焦面杂散光分布的均匀程度得到有效的改善。

(4) 通过减小圆顶天窗开口宽度，可使得其PSNIT最大降低约1个数量级；调焦时副镜位置变化和望远镜指向高度角变化对望远镜PSNIT的变化小于3.5%。

(5)考虑杂散光效应的该望远镜观测SNR分析结果说明：满月方位与望远镜指向夹角θ=25°时，仿真对R波段15等星观测，曝光时间15～150s，“定性措施”和“定量措施”组合使用可使观测SNR提高约147%，望远镜探测极限有望提高2.6星等。同等观测条件在其它方位，观测信噪比和探测极限星等也有明显提高。

本文所采用的针对兴隆1m光学望远镜的杂散光效应计算和评价方法，不仅为兴隆1m光学望远镜杂散光效应优化设计提供参考和依据，同样可应用于其他天文光学望远镜。

致谢：在本文的写作过程中，国家天文台胡景耀和姜晓军，对天文观测相关原理给予了详细指导，并与作者针对观测中的杂散光问题进行深入的讨论，在此表示感谢。

[1] 1m telescope specifications [M]. Tucson: EOS technologies,Inc,2007：1.

[2] Tracepro user manual [M].V3.3, Littleton: Lambda Research Corporation,2003:512.

[3] Pompea.The Management of Stray Radiation Issues in Space Optical Systems [J].Space Science Reviews, 1995,74:181-193.

[4] Tracepro user manual [M].V3.3, Littleton: Lambda Research Corporation,2003:11.

[5] Tracepro user manual [M].V3.3, Littleton: Lambda Research Corporation,2003:39.

[6] Michael Bass.Handbook of optics [M]. New York: McGraw-Hill, Inc,1995:371.

[7] B Patterson. Analysis of Scattered Light for VISTA[A]. Proc SPIE,2003,4842:116-120.

[8] W Sigmund. Sloan Digital Sky Survey 2.5-m telescope[A]. Proc SPIE,1998,3352:653-663.

[9] S Ellis. ATST stray and scattered light analysis[R]. Photon Engineering LLC, 2003.

[10] The New CCD Astronomy [M]. WA 98019 USA: New Astronomy Press,2002:89.

[11] Pierre Y Bely. The design and construction of large optical telescopes [M]. New York :Springer, 2003:24.

[12] The New CCD Astronomy [M], WA 98019 USA: New Astronomy Press,2002:329-332.

[13] ZHOU Xu.A Method of Sky Quality Evaluation Using Wide Field Photometry [J]. ACTA ASTROPHYSICA SINICA,2000, 20(2):216-224.

[14] Versa ray System Manual [M]. Princeton: Princeton Instruments,2006:47.