小行星初轨计算的Fortran程序设计

陈姗姗,尹红星

(山东大学威海分校空间科学与物理学院，山东 威海 264209)

小行星是早期太阳系残留下来的物质，对太阳系初期的演化研究有重要意义[1]。小行星初轨计算是研究小行星必不可少的环节，初期的有效预报是其发现的保证。目前共发现永久编号小行星21万多颗。

国际小行星中心(MPC)[2]对小行星进行编号确定工作，为方便观测者观测，开通了免费的网上服务如小行星轨道预报、轨道根数下载等。意大利几位科学家在网上提供的小行星轨道计算免费软件包OrbFit[3]是现在较常用的软件包。国外有几个网站[1]可以提供小行星历表服务或轨道根数下载服务，如意大利Pisa大学的空间力学组在AstDys小行星动力学网站[4]给出了永久编号小行星、有多次观测记录和单次观测记录小行星的轨道根数和其他固有根数的下载，美国洛威尔天文台的Edward Bowell博士在网上免费提供完整且每天更新的小行星高精度吻切轨道根数[5]，美国宇航局喷气推进实验室(JPL)免费提供的HORIZONS[6]太阳系数据和历表服务，可以通过远程登录、电子邮件及在线使用方式获取包括小行星在内的太阳系内天体的各种数据资源，包括轨道根数及星历表计算。

小行星的运动研究是我国的传统研究课题[7]。国家天文台BATC项目组1995年5月开始实施大视场CCD小行星巡天计划(SCAP)[8]，已建立了小行星发现数据库，小行星巡天数据库正在建设中。另外紫金山天文台也开展小行星观测工作，建立起包括观测资料处理、初轨计算、摄动计算、轨道改进和位置预报等几个系统的软件包。南京大学天文系也有了规模较小的软件包。

小行星的定轨工作离不开太阳系历表的使用。自1984年起国际上普遍采用JPL提供的高精度历表。紫金山天文台现已在其网站[9]上提供电子天文历表服务。我校于07年建成1m口径的赤道式反射望远镜[10]，并利用该望远镜进行小行星搜寻工作。

文章分3部分。首先简要给出文中采用的两种初轨计算方法的原理；然后给出两种方法的实现及适用范围；最后给出对Laplace方法流程的调整。

1 初轨计算原理

初轨计算方法很多，从根本上可以分为Laplace型和Gauss型[11]，Laplace型先设法从三次角观测量求解某时刻的位置速度矢量，Gauss型则从三次角观测量求解两个时刻的位置矢量。下面简要介绍文中使用的改进的Laplace和Gauss方法的计算原理。

1.1 二体问题

小行星相对太阳的相对运动方程：

(1)

小行星和太阳组成的系统所受合外力为零、合力矩为零、系统内只有保守力作用，分别应用动量守恒定律、角动量守恒定律、能量守恒定律引入这6个常数，即为轨道根数。轨道根数能反映小行星的运动特性，通常选择为轨道半长轴a、偏心率e、轨道倾角i、升交点黄经Ω、近地(星)点幅角ω、平近点角M(近地点时刻τ)。对小行星运动的椭圆轨道，轨道根数具有明显的几何意义，其中a、e为描述轨道大小和形状的参数，i、Ω、ω为描述轨道位置的参数，M(τ)给出小行星的具体位置。

1.2 几何关系

(2)

1.3f、g形式

f、g级数表达式见文献[11]。

1.4 改进的Laplace方法主要迭代方程

由三次观测的几何关系得：

νixi=λizi+pi

νiyi=μizi+qi(i=1,2,3)

(4)

其中，pi=νiXi-λiZi；qi=νiYi-μiZi

(5)

式中λ，μ，ν及下面未注释的量的意义见文献[11]。将(3)式代入(4)式，整理得：

νifix-λifiz+νigix′-λigiz′=pi

νifiy-μifiz+νigiy′-μigiz′=qi(i=1,2,3)

(6)

迭代求解[11]即可求得中间时刻的位置速度值。迭代初值取上面f、g级数形式的第1项。

1.5 改进的Gauss方法主要迭代方程

小行星在二体问题模型下的轨道是过日心的固定平面，并利用几何关系整理得：

λ1n1ρ1-λ2ρ2+λ3n3ρ3=n1X1-X2+n3X3

μ1n1ρ1-μ2ρ2+μ3n3ρ3=n1Y1-Y2+n3Y3

ν1n1ρ1-ν2ρ2+ν3n3ρ3=n1Z1-Z2+n3Z3

(7)

n1、n3及下面各未标注量的意义见文献[12]。

上方程组消去n1ρ1,n3ρ3再利用f、g关系求出n1,n3的级数表达式，整理得：

(8)

为求得ρ2,r2，由矢量关系得ρ2,r2的另一关系式：

(9)

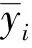
(10)

(11)

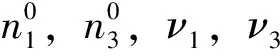
2 程序实现

2.1 时间系统与坐标系统

时间系统选用UT世界时，程序中通过美国海军天文台(USNO)的novas程序包[13]转化为TDB儒略日形式。坐标系统选用J2000赤道坐标系和黄道坐标系。

2.2 运行环境

为统一形式，程序编写使用f77版本，在linux系统的fedora(2.6.231-42.fcc8)下编译运行，编译器为系统自带的gcc(4.1.2)。

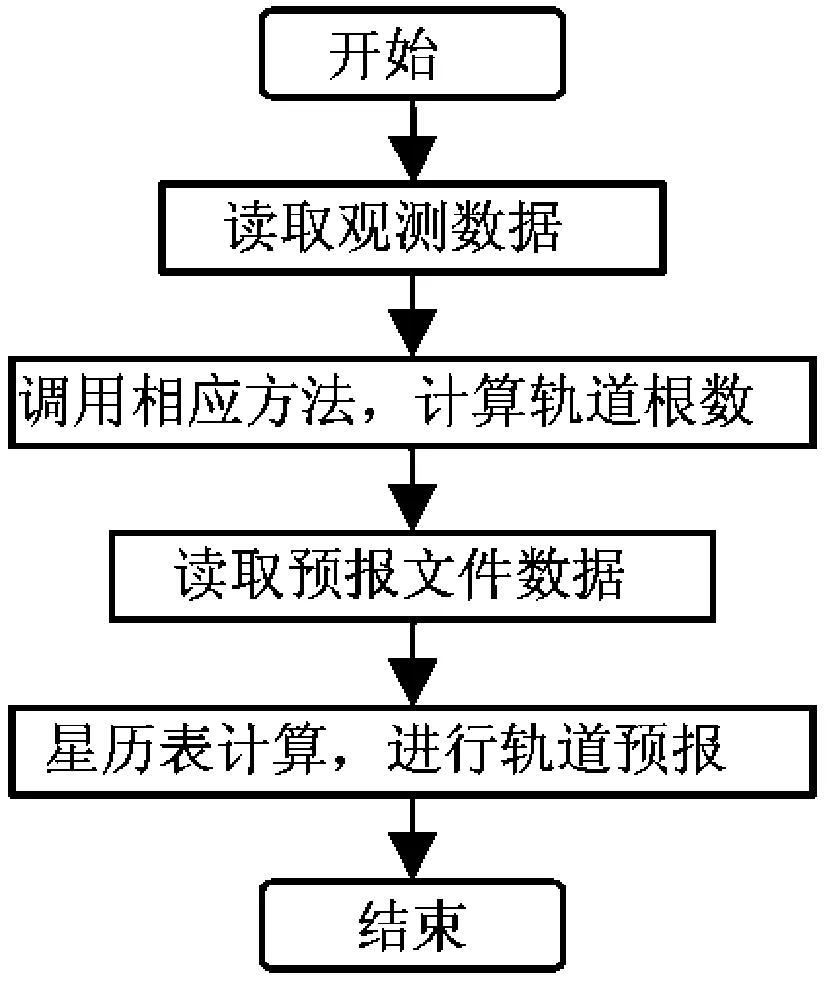
图1 主程序流程图Fig.1 Data flow in the main program

2.3 运行准备及要求

程序使用的是DE405星历表[14]，该星历表基于国际天文协会(IAU)所建立的ICRF[15]参考架。星历表的使用借用了USNO的novas程序包和JPL提供的星历使用程序selcon.f。使用前需安装相应的星历文件及星历表使用程序包。

程序用三次角观测资料进行初轨计算，运行前建立观测文件obs，格式与MPC相同。对小行星进行位置预报需建立程序要求格式的pre文件。预报结果放在preorb文件中。

2.4 主要程序流程图

图1给出主程序流程图，对较长时间间隔的三次观测资料，可使用改进的Laplace和Gauss方法，短时间间隔的观测资料可使用文中调整的Laplace方法。图2和图3为改进的Gauss和Laplace方法的程序流程图。

图2 改进的Gauss方法流程图

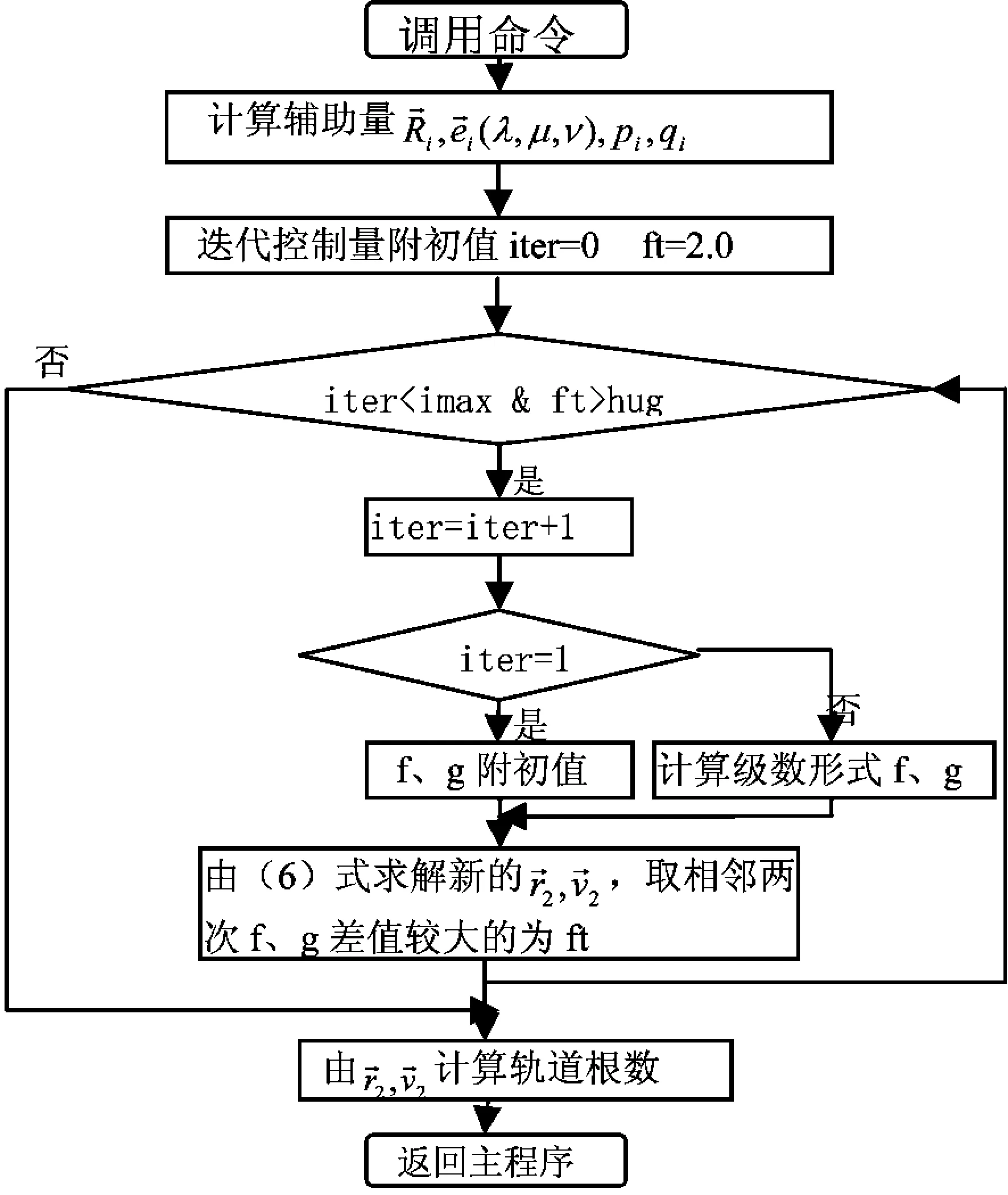
图3 改进的Laplace方法流程图，iter,imax,ft,hug为迭代控制量

2.5 主要子程序效果验证

首先对由某时刻位置速度矢量计算轨道根数及星历表计算程序进行了联合测试，图4为测试结果。由于初轨计算采用的是二体模型，而实际上在摄动力作用下小行星的真实轨道是一族吻切轨道的包络线，观测点计算出的轨道与真实轨道相切，因此如图出现观测点附近精度高，距离半周期时偏离很大的现象，另外采用数据点少也是造成计算轨道与真实轨道偏离的原因。图示两方向最大偏移量小于2.0′,可以认为两个主要子程序效果良好。

对改进的Laplace和Gauss方法进行验证时采用了00014号小行星不同时间间隔的模拟观测数据，验证结果见表1。由表中数据可见，对于不同时间间隔的角观测数据，两种方法计算效果不同，都有随时间间隔缩小变坏的趋势。即改进的Laplace方法和Gauss方法对小行星进行初轨计算时，只适用于弧段不是很短的情况，此时两种方法效果接近，由于程序中Gauss方法考虑了光行差，且Laplace方法f、g阶数只取了四阶，高斯方法稍优于拉普拉斯方法；对短时间隔的观测数据(小时量级间隔)两种方法计算的轨道根数都有较大偏离，因此无法进行有效的轨道预报。

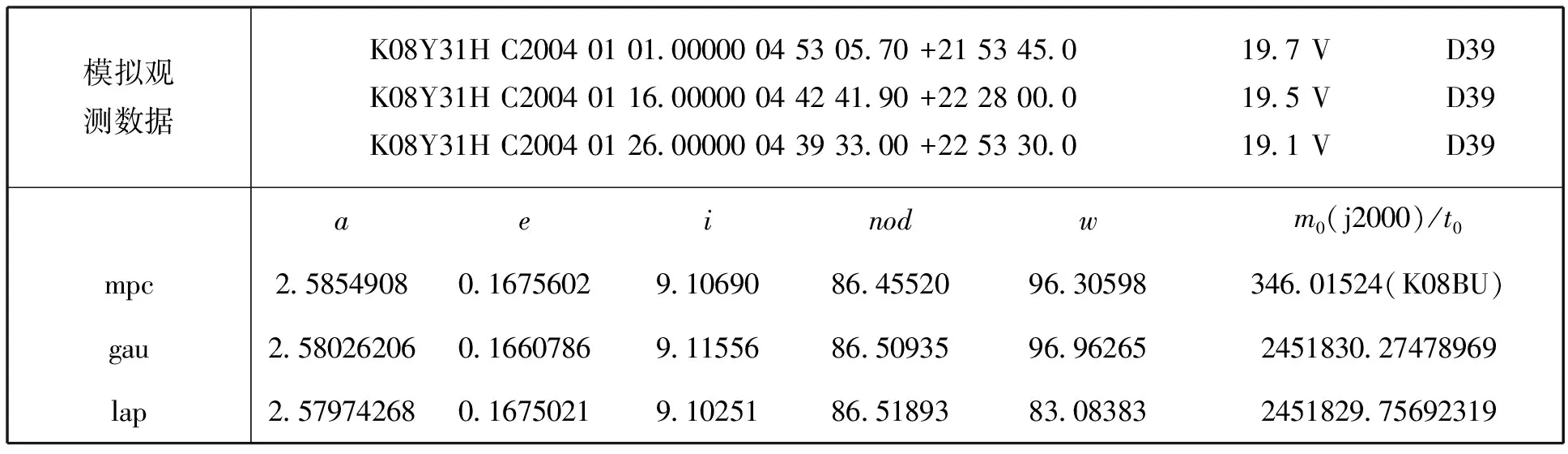
表1 初轨计算方法比较.表中模拟观测数据是MPC小行星历表服务生成的00014号小行星的相应数据。每组数据给出MPC轨道根数文件中列出的轨道根数及改进的Laplace和Gauss方法得出的轨道根数。其中MPC给出第6个轨道根数为平近点角，程序给出的是过近点时刻Table 1 Comparison of initial-orbit calculation methods. The simulated observation data are of Asteroid No.00014 generated with the Minor Planet & Comet Ephemeris Service(MPC) online. The table gives the orbital elements from Laplace method,Gaussian method,and MPC orbit database. The sixth orbit element from the MPC is the mean anomaly while the program gives the mean anomaly time.

续表

模拟观测数据K08Y31HC200401010000004530570+2153450K08Y31HC200401030000004512180+2158080K08Y31HC200401050000004494380+2202340197V195V191VD39D39D39aeinodwm0(j2000)/t0mpc25854908016756029106908645520963059834601524(K08BU)gau264289220213260582886087052418385090245170953345543lap264266890213167682911287050568389406245170990843509模拟观测数据K08Y31HC200401010000004530570+2153450K08Y31HC200401020000004521310+2155560K08Y31HC200401030000004512180+2158080197V195V191VD39D39D39aeinodwm0(j2000)/t0mpc25854908016756029106908645520963059834601524(K08BU)gau318423930400148880783487123627660508245114841533498lap318364340400061480756487125957659389245114904540179模拟观测数据K08Y31HC200401010000004530570+2153450K08Y31HC200401010416704530350+2153500K08Y31HC200401010833304530120+2153560197V195V191VD39D39D39aeinodwm0(j2000)/t0mpc25854908016756029106908645520963059834601524(K08BU)gau153949250418554502620210157304489756245234382144170lap101329110032735500107111769518977016245265899135827

3 Laplace方法流程的调整

为了使程序实现用短时间间隔的角观测资料进行轨道预报，对流程相对简单的Laplace方法进行调整。

3.1 调整原理

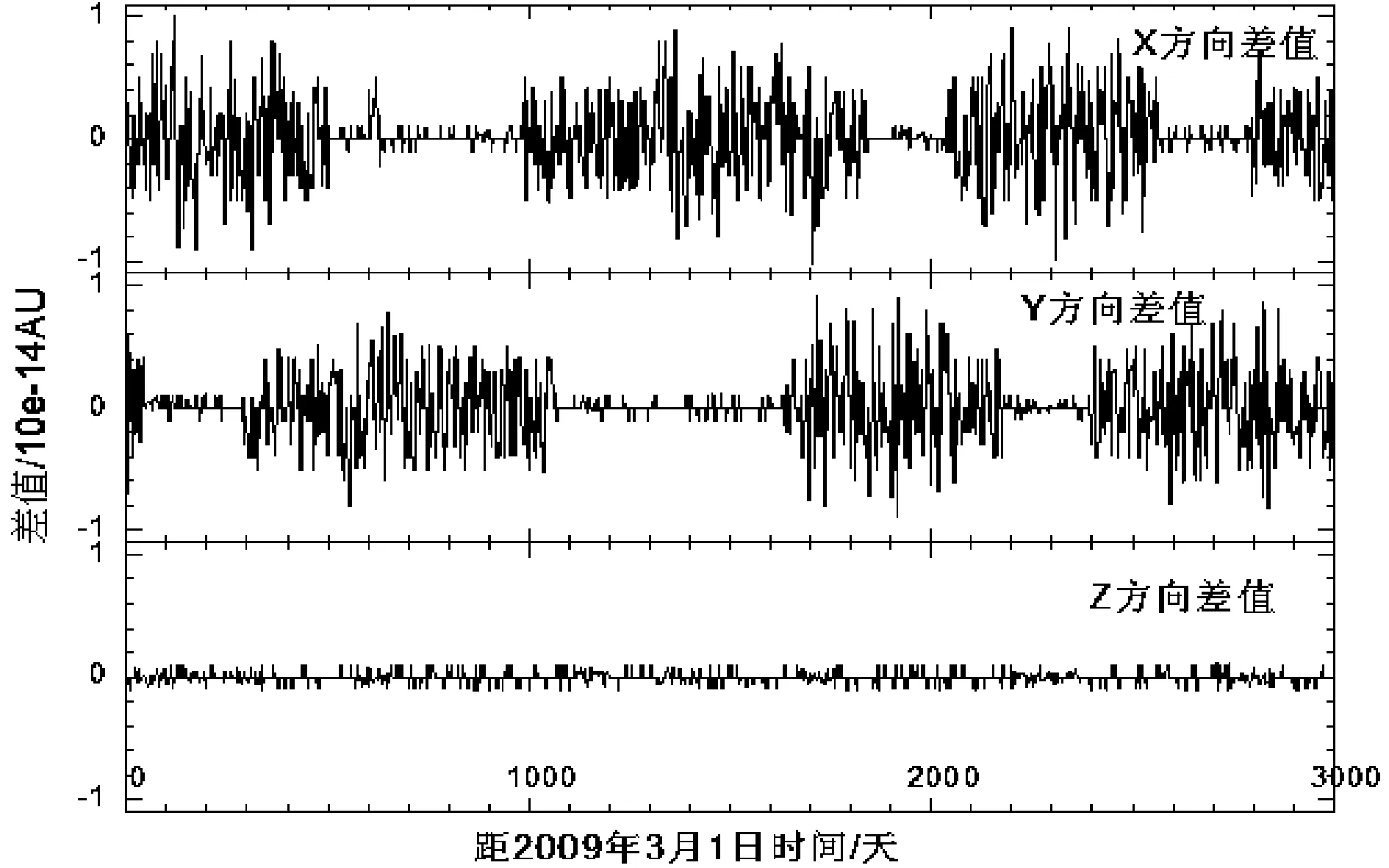
图5 几何关系验证Fig.5 Test chart for geometric positions.The vertical coordinates are for the differences of the three components of e+-s，respectively.The comparisons are made to the data from DE405 covering 3000 days starting from March 1,2009

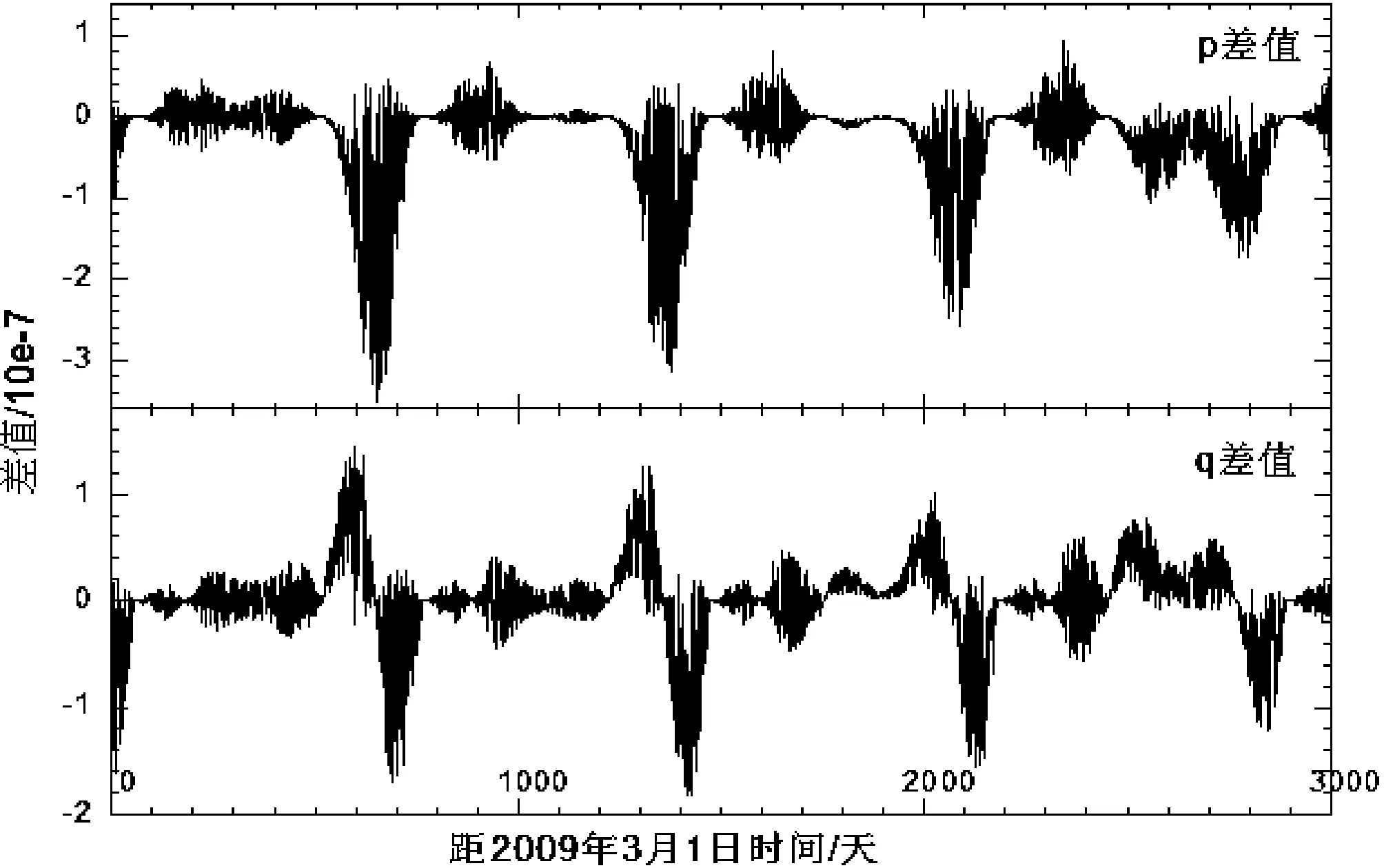
图6 p、q关系验证

由图5可见，三方向的差值最大为10e-14量级，可以认为几何关系是成立的。但图6中p、q的差值在10e-7量级，相比几何关系的差值很大，对p、q对求解的影响进行了测试(表2)。由表中数据可见，p、q在此量级上的线性变化对结果影响不大，非线性变化使求解值有较大波动，方程组对p、q变化敏感。p、q关系本身的差别造成了求解结果的较大偏离，因而直接求解不能得出很好的结果，为此求解之前需要对p、q进行调整。

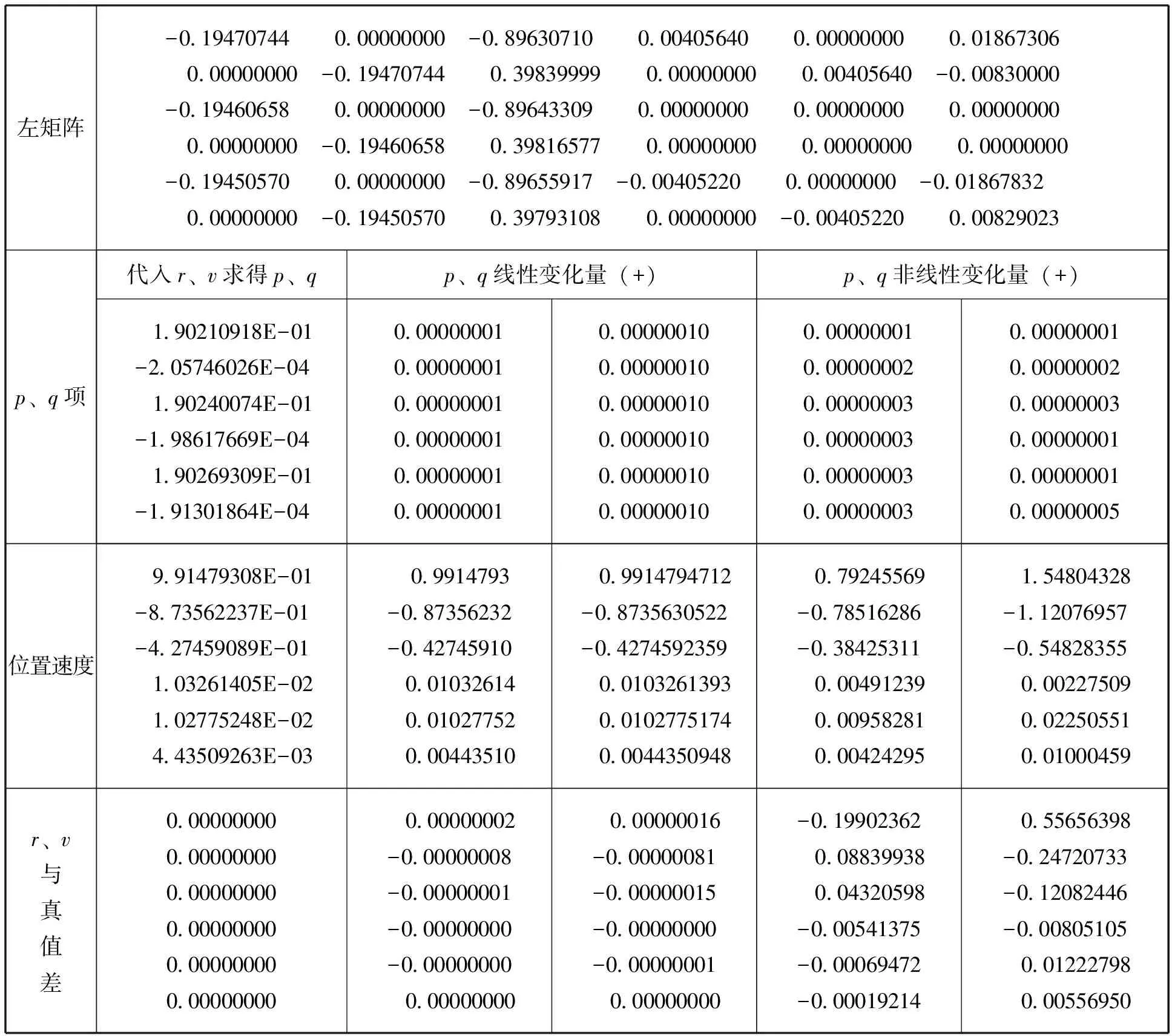
表2 p、q变化对结果影响.表中求解方程为Laplace方法的主要方程(6)式，

3.2 流程调整方法

增加调整项：考虑到p、q共6个量，如果每个量进行10次调整，将要进行一百万次迭代计算过程，一次运行要几个小时。程序采用折中办法，只对p做调整，q调整取决于p，以减少程序运行时间。

判断p、q调整是否良好的条件：

条件1：比较由计算得到的赤经赤纬与观测值的差别是否足够小；

条件2：由结果r、v计算出轨道根数，剔除明显不合适的调整项(如a<0，e<0,e>1)。单用上面两个条件求出的结果计算轨道根数并进行轨道预报不能得到预期结果；

条件3：加入轨道预报项，挑选预报值与观测值最接近的调整计算结果。

3.3 调整后的Laplace程序流程及预报效果

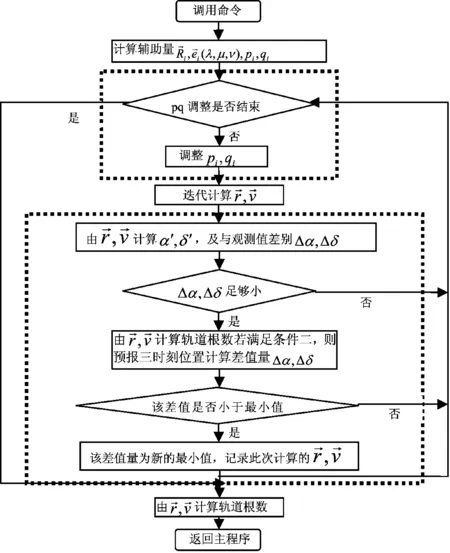
图7 调整后的Laplace流程图.虚线框内为所加调整部分

程序分别用火星星历表计算值和山东大学威海天文台数据进行了测试。表3、表4给出两测试结果，校天文台望远镜视场为6′，程序可以给出3天内的有效预报值，指导后续观测。

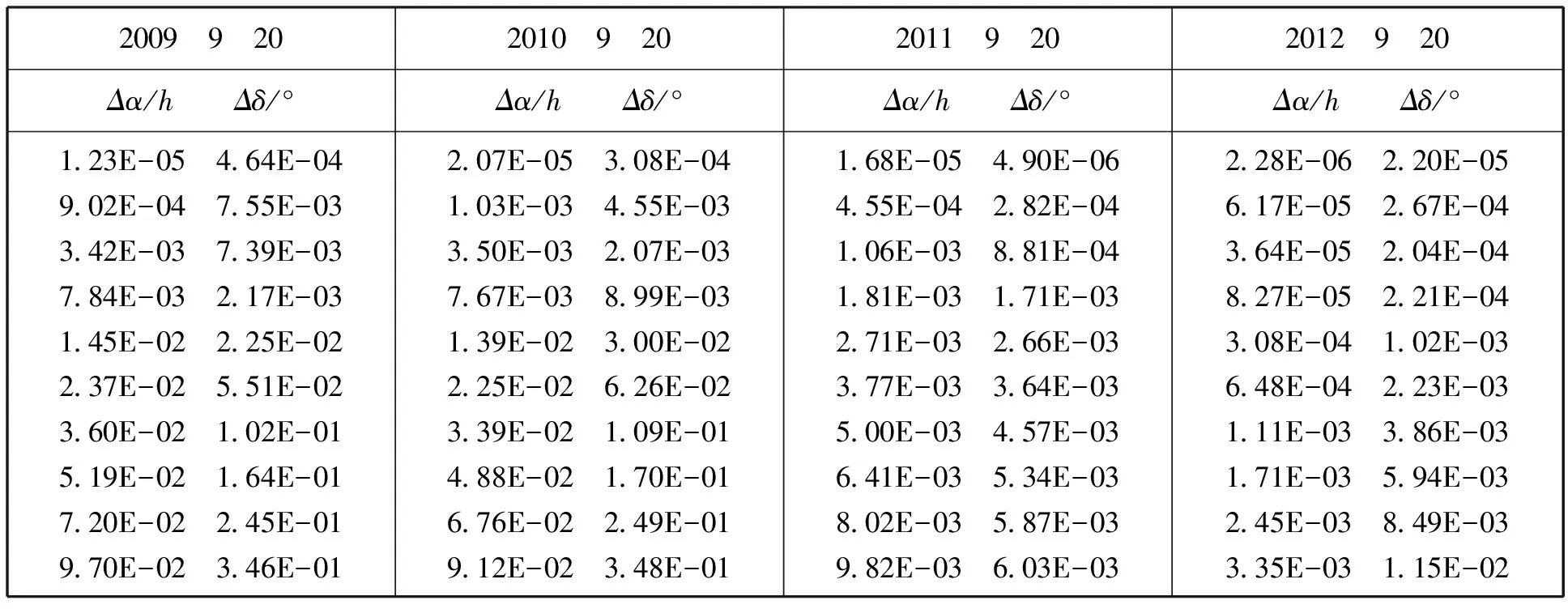
表3 火星数据测试结果.表中第一行为日期，取该天0.5h、1.0h、1.5h的火星星历计算值为模拟观测数据，进行10天的预报，下面对应列给出程序预报值与星历表计算值在赤经赤纬方向上的差值

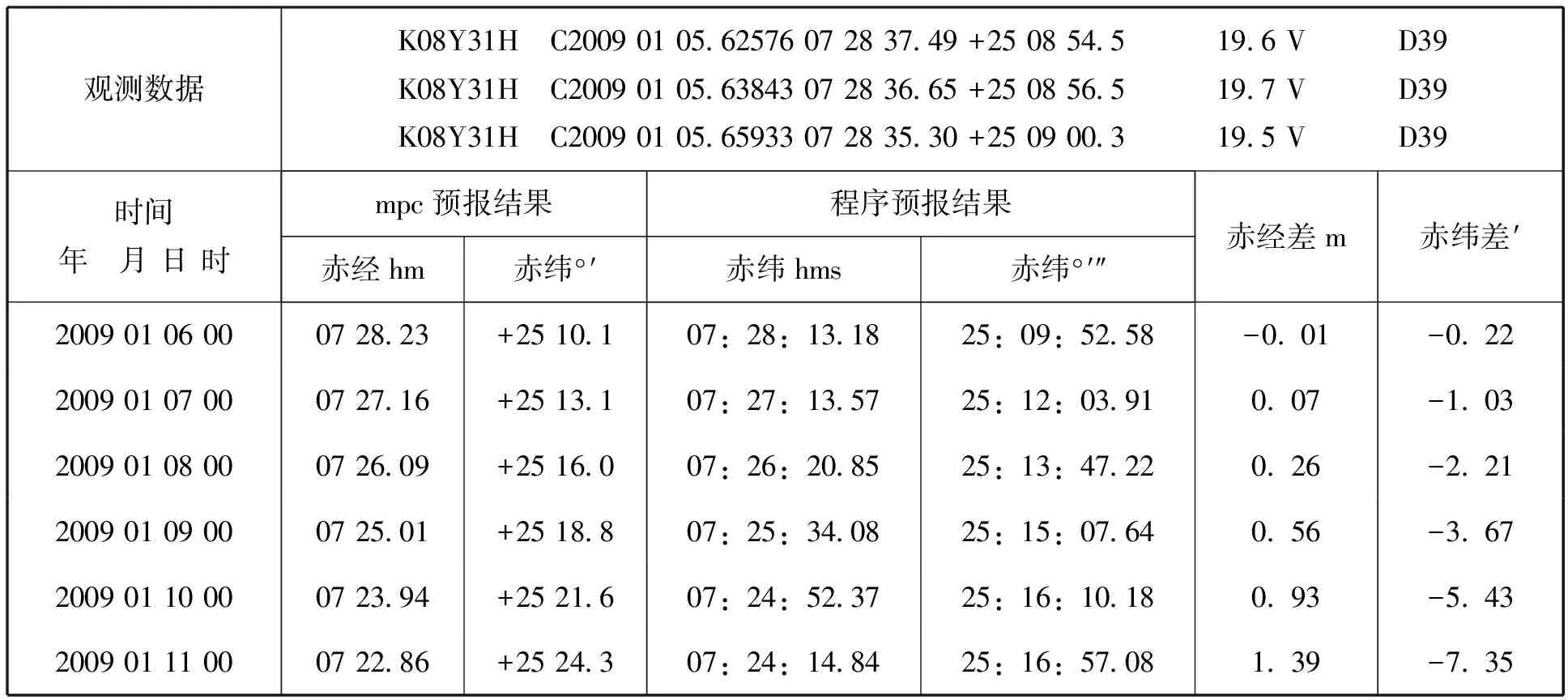
表4 校天文台数据测试结果.表中给出我校天文台1m口径望远镜的一组观测数据，给出所列时刻程序预报结果与MPC历表生成服务相应结果的差值

4 结 论

初轨计算原理清楚，方法很多但根本上可以分成Laplace型和Gauss型。Fortran程序实现了改进的Laplace和Gauss方法，给出其实现流程。对两程序的测试选用了00014号小行星，该小行星属于主带小行星，有代表性地给出两种方法的使用范围：初轨计算属于短弧定轨，但弧段不宜太短，对两天间隔以上的三次角观测资料可以进行有效的轨道预报；对更短弧段的观测资料由于两种方法计算出的轨道根数偏离太大，不能进行有效的预报以指导观测。

为了可以利用一天内的三次角观测数据进行轨道预报指导后续观测，对流程较简单的Laplace方法进行了调整。通过对该方法主要原理的验证，找出问题的所在： Laplace方法主要迭代方程组对方程组右矩阵的变化较敏感，而方程右矩阵本身的不确定度导致无法求得理想的位置速度矢量，因而相应轨道根数有较大偏离，也就无法进行有效的轨道预报。因此程序考虑增加主要迭代方程右矩阵的调整项和反馈项，经调整后可以指导我校天文台的小行星观测，初步实现预报功能。

要改善初轨计算结果需要考虑更多因素如进行观测资料预处理[16]。对多次观测可以挑选观测误差较小的观测值，或者将统计原理应用于初轨计算，提高初轨计算的精度。

[1] 朱进，高建，关敏，等.小行星的搜寻和定轨[J].云南天文台台刊, 2002(3):17-20.

ZHU Jin,GAO Jian,GUAN Min,et al.Asteroid Searching and Orbit Determination[J].Publications of Yunnan Observatory,2002(3):17-20.

[2] http://www.cfa.harvard.edu/iau/MPC.html.

[3] http://adams.dm.unipi.it/～orbmaint/orbfit/.

[4] http://hamilton.dm.unipi.it/astdys/index.php?pc=4.

[5] ftp://ftp.lowell.edu/pub/elgb/astorb.html.

[6] http://ssd.jpl.nasa.gov/?horizons.

[7] 王绶琯.20世纪中国学术大典/天文学[M].福州：福建教育出版社，2002:75-77.

[8] http://batc.bao.ac.cn/work/jobs/work/work10.htm.

[9] http://159.226.71.170/dianzili.htm.

[10] http://astro.wh.sdu.edu.cn/apparatus/ShowArticle.asp?ArticleID=4.

[11] 刘林，胡松杰，王歆.航天动力学引论[M].南京：南京大学出版社,2006:45-52.

[12] 易照华.天体力学基础[M].南京：南京大学出版社,1993: 96-120.

[13] http://aa.usno.navy.mil/software/novas/novas_f/novasf_intro.html.

[14] ftp://ssd.jpl.nasa.gov/pub/eph/planets/usrguide.

[15] 乔书波，李金岭，孙付平，等. ICRF的现状分析及未来的发展[J].天文学进展,2007(2):147-160.

QIAO Shu-bo,LI Jin-ling,SUN Fu-ping,et al.Analysis of Present Status of ZCRF and ZCRF in Future[J].Progress in Astronmy,2007(2):149-160.

[16] 王威，于志坚.航天器轨道确定——模型与算法[M].北京：国防工业出版社,2007. 87-115.