基于免疫粒子群算法的地磁特征区域选择

焦 巍,刘光斌,张金生,张 博,乔玉坤

(第二炮兵工程学院,西安 710025)

0 引 言

“惯性制导+地形匹配”或“惯性制导+地形匹配+卫星导航”的组合制导方式,是目前巡航导弹最常用的制导模式,其中地形匹配制导和卫星导航是辅助制导,用以修正惯性制导的累积误差。但是,无线电导航信号会受到敌方的屏蔽和干扰;巡航导弹跨海域、平原、沙漠、森林等飞行时,由于地形的灰度和纹理基本相同,地形匹配也难以实现。因此,需要寻找自助式、无长期积累误差、具有较强抗干扰能力的导航定位技术。随着大地测量技术的进步,具有隐蔽性好、成本低、精度适中的地磁匹配制导技术,近年来受到许多学者的关注[1-3]。提出地磁匹配制导与惯性制导相结合,通过一定的匹配算法得到最佳匹配位置,再将此位置信息校正惯导系统,供制导计算机实时修正弹道,达到精确制导的目的。

由于地磁场具有空间各异性,地磁匹配的解算结果与所在地磁场区域的磁场特性紧密相关,在某些区域并不适合进行地磁匹配制导。并且,由于地磁图数据库的空间局限,地磁匹配时采取间断性匹配,即匹配只在特定区域内进行,所以为了保证地磁匹配的精度和准确性,需要预先在待匹配的地磁场区域内进行特征区域的选择,即在已知的地磁场区域内,选出若干个一定大小、空间连续分布的匹配区,使得地磁场空间变化在这些区域内相对最显著。周贤高等[4]通过统计分析,给出了地磁匹配特征区域选取的经验性准则,但如何在已知的地磁场区域内,进行快速、智能化的区域选择却鲜见报道。

粒子群优化(Particle Swarm Optimization,PSO)算法是美国的J.Kennedy和R.Eberhart于1995年提出的一种群智能优化算法[5-6],因为其具有操作简单、全局搜索能力强、收敛速度快等特点,已广泛应用于求解各类优化问题。而地磁特征区域选择问题可以归结为一个在地磁场区域内,若干局部区域的优化组合问题。本文将采用基于群智能随机搜索技术的粒子群优化算法,进行地磁特征区域选择的探索性研究。

1 特征区域选择策略

地磁图通常以离散点的方式表示地磁场的空间变化规律,每组离散点包括位置和磁场强度信息。地磁图经过一定的数据处理方法都可以变换为标准网格形式表示,即位置点列由两组间距相等、互相垂直的平行线组成的规则网格。网格坐标(i,j)(i,j为自然数)对应地理坐标纬、经度,每个网格坐标处都对应有地磁场强度值fi,j。如果将PSO算法中的粒子编码为2维的网格坐标(i,j),则完全可以采用PSO算法,依据一定的评价函数,在已知的地磁图中进行特征区域的优化选择。

1.1 评价函数

本文侧重于对地磁图的整体性能评价,故采用基于统计特性分析的粗糙方差比 σ/δ作为某一特征区域地磁起伏丰富度的衡量指标[4],即PSO算法的评价函数。σ/δ值小,则表示采样点间变化较小,但整个区域可能有较大而缓慢的起伏,地磁场较平滑,不宜匹配。反之,σ/δ值大,表示相邻采样点间的变化比整个区域起伏相对增大,容易匹配。

设某一地磁场区域 Ω的地磁强度集合为V:V={fi,j},其中f i,j为网格坐标(i,j)处的地磁场强度值;(i,j)对应一组地理坐标,(i,j)∈U,U={(i,j)|1≤i≤M,1≤j≤N},(M,N)表示该地磁场区域 Ω的大小。标准差 δ主要反映了地磁场强度的离散程度和整个地磁场区域总的起伏程度,其定义为:

地磁图绝对粗糙度σ反映整个区域平均光滑程度,刻画较细微的局部起伏,其定义为:

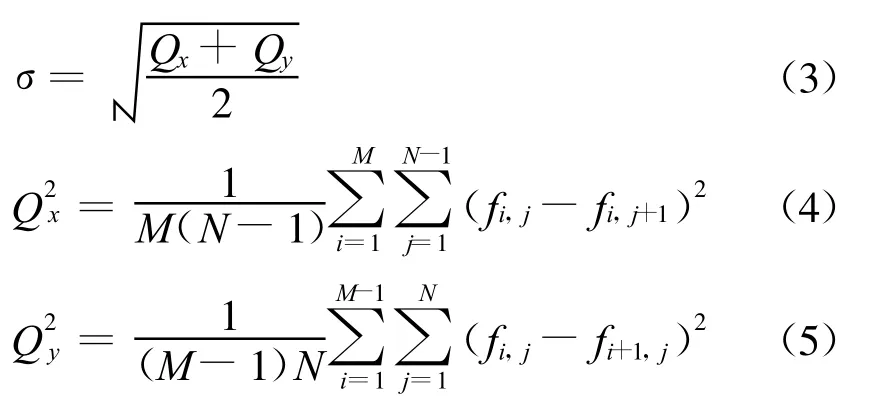
1.2 搜索方法

地磁特征区域的大小可根据对匹配长度的限定值和惯导最大漂移误差确定,假设在标准网格图中为m×n网格大小。在整个(M,N)地磁场区域中随机初始化Nm个粒子,以每个粒子为中心扩展成m×n网格大小的Nm个待选区。运用PSO算法通过进化迭代,搜索出该地磁场区域中 σ/δ值最优的一个(m,n)区域作为最优匹配的地磁特征区,完成一次独立搜索。下一次的最优特征区选择,应该是在地磁场区域(M,N)中去除上一次搜索所得的(m,n)区域之后获得的,但是为了保证搜索所得各特征区域之间的连通性,从整个地磁场区域中,只去除由已获得特征区域中心点向外扩展的(m-1)×(n-1)个网格点,再在剩余区域内继续执行新一轮搜索,直到满足搜索终止条件。搜索终止条件可以根据需要,进行不同的设置。这里建议,如果满足:搜索所得特征区域的某项指标已不能达到要求的阈值范围;或者搜索所得特征区域,从整个地磁场区域的一端贯通到另一端,便可终止搜索。

地磁场的空间分布复杂,磁场强度值的空间变化类似于一个搜索域内的多峰值函数。而标准PSO算法在解存在大量局部最优点的多峰值函数时,因多样性损失极易陷入局部最优点。所以,必须对标准PSO算法进行改进,以适应地磁场特征分布的特点。

2 免疫PSO算法

免疫算法是一种受生物免疫系统的启发而设计出来的一种对多峰值搜索具有全局寻优能力的智能优化算法,能够快速、高效地找到各个极值点,但其计算复杂。故而,结合免疫算法更强的全局寻优能力和PSO易操作特点的免疫PSO算法,成为近年来智能优化算法的热点之一。一般而言,免疫PSO算法首先采用标准PSO进化方程进化粒子速度、位置,即

其中i=1,2,…,Nm,d=1,2,…,D,Nm,D分别为粒子群规模和搜索空间的维数。ω是惯性权值,一般随迭代次数从0.9到0.4线性递减;c1,c2是非负常数,通常取值为2.0;rand1,rand2是介于[0,1]之间服从均匀分布的随机数;Pi=(pi1,pi2,…,piD)是粒子i当前所经历的最优位置,称为个体最优位置;Pg=(pg1,pg2,…,pgD)是群体中所有粒子所经历的最优位置,称为全局最优位置。

在如上进化过程中,每次迭代进化后记录最优值Pg作为免疫粒子(抗体),当标准PSO进化不满足结束条件时,进行免疫操作,更新粒子群,之后继续按照式(6)、(7)进化,直至达到终止要求。

本文在前人关于免疫粒子群算法的工作基础上[7],结合地磁特征区域选择的特点,给出免疫粒子群算法主要计算流程如下:

Step 1 随机初始化粒子群中粒子的位置与速度,生成Nm个粒子;

Step 2 计算每个粒子的适应值;

Step 3 如果粒子的适应值优于Pi的适应值,则 P i更新为新位置,反之P i保持不变;如果粒子的适应值优于Pg的适应值,则Pg更新为新位置,反之Pg保持不变;

Step 4 根据式(6)、(7)更新粒子的位置与速度;

Step 5 进行速度、位置限制。当 Vi＞Vmax或Vi＜-Vmax,则令 Vi=Vmax或 Vi=-Vmax;当 Xi＞Xmax或Xi＜Xmin,则令 Xi=Xo,其中 Xo为搜索区域的中心位置坐标;

Step 6 生成免疫记忆粒子(抗体)。计算当前粒子(抗体)群体中粒子(抗体)的适应值,并将Pg作为免疫记忆粒子(抗体)存入记忆库,判断是否满足结束条件,若满足则输出最优值Pg,否则,继续;

Step 7 更新粒子(抗体)。新粒子(抗体)由以下方式产生:

(1)随机产生NR个新粒子(抗体);

(2)从记忆库中根据基于粒子(抗体)浓度的概率选择式(8)～(9),选出N0个粒子(抗体),N0=Nm-NR;

(3)免疫接种。将进化过程中的 Pg作为免疫疫苗,分解疫苗,其分量即为提取的免疫基因。从种群中随机选择NV个粒子,进行免疫接种;

(4)免疫检测。如果接种后的粒子优于之前粒子适应值,则保留接种粒子,反之,取消免疫接种。生成新一代粒子(抗体)后,转向Step2。

式中Nl表示免疫记忆库的大小。

如何确定上述参数Nl、NR和NV比较困难,但是它们对算法本身影响不显著。通过大量仿真实验,这里给出一组经验取值。Nl=2Nm;模拟自然界克隆选择过程0.05～0.20的淘汰率NR=0.05Nm;NV=0.2Nm;免疫疫苗(Pg)被分割成■D/NV」份免疫基因,其中■」表示向下取整。

3 仿真实验

地磁场有七个主要的特征量:总磁场强度 F、水平强度H、东向强度Y、北向强度X、垂直强度Z、磁偏角D和磁倾角I。根据乔玉坤等人[8]的研究成果,结合当前地磁测量传感器应用现状,本文以总磁场强度F作为地磁特征区域选择的匹配特征量。

以我国北部某沿海海域地磁数据为例,地磁图数据大小为60×60网格。每次搜索的特征区域大小取为13×13网格。粒子群规模Nm=30,最大速度 Vmax=10,最大迭代次数设为800次。实验结果如图1所示,图中曲线表示总磁场强度值的等值线。免疫PSO算法搜索所得的最优地磁特征区总共由8个网格为13×13的地磁区域组成(图中实线方框)。

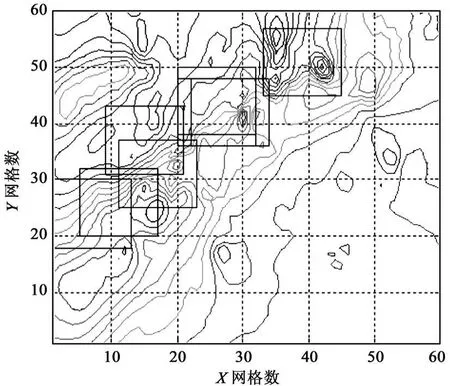
图1 某海域地磁特征区域选取结果:免疫PSO算法Fig.1 The selective result of a certain sea geomagnetic characteristic areas:Immune PSO algorithm

为了比较文中免疫PSO算法优化存在大量局部最优点函数的优越性,保持粒子群算法基本参数设置不变,在相同的实验环境中,采用标准PSO算法搜索所得的最优地磁特征区域结果如图2所示。从图2中可以看出,由于标准PSO算法多样性的损失,易于陷入局部最优点,而致使其搜索所得的最优地磁特征区域出现了“虚假”的最优区,即中心坐标为(32,19)的一块特征区。

图2 某海域地磁特征区域选取结果:标准PSO算法Fig.2 The selective result of a certain sea geomagnetic characteristic areas:Standard PSO algorithm

我们知道,地磁信号是弱信号,地磁测量系统不可避免的受到各种干扰的影响,其中环境干扰影响最为严重。为了验证所得特征区的可行性和有效性,这里以高斯噪声仿真地磁实测环境中的干扰,在不同噪声强度下,对每个特征区采用经典的均方差算法——MSD算法[9],进行地磁匹配仿真。同时,考虑到沿不同方向地磁特征有所不同,为了平滑沿某一个方向可能带来的局限性,实验随机产生两条不同路径分别进行1000次仿真,实验所得的结果如表1、表2所示。而整个60×60网格的地磁场区域,在相同噪声环境下的匹配概率,即整个地磁场区的平均匹配概率,如表3所示。表中的匹配概率是指使匹配结果控制在3个单位网格距离的概率。

表1 不同噪声环境下沿路径一的匹配概率Table1 The matching probability along route 1 under different noise situations

由表1～表3的仿真实验结果可见,在文中所选择的特征区内,地磁匹配概率远高于整个地磁场区的平均匹配概率,特别是随着噪声强度的增加,这种优势愈发明显。也就是说,经过文中所给选择方法选取的匹配特征区,在具有较强噪声干扰的地磁环境中,相对其它地磁场区域具有更高的地磁匹配精度,能够使得地磁匹配制导系统的性能得到更好的发挥。从图1中也可以直观地看出,相对其它区域,在应用免疫PSO算法搜索选取的特征区域内,地磁场总强度的等值线密集、大小起伏变化显著,显然是该地磁场区内适宜地磁匹配的最优特征区域。

表2 不同噪声环境下沿路径二的匹配概率Table 2 Thematching probability along route 2 under different noise situations

表3 不同噪声环境下整个地磁场区的匹配概率Table 3 Thematching probability of the whole geomagnetic area under different noise situations

4 结 论

结合地磁场强度值的空间分布特性和免疫粒子群强大的全局搜索能力,本文将免疫粒子群优化算法应用于地磁特征区域的智能化选择。仿真实验的结果表明,根据文中给出的搜索策略选取的地磁特征区既能够达到匹配概率的最优化,又保证了特征区域的连通性,具有一定的工程实际应用价值。文中采用粗糙方差比作为地磁场变化丰富度的衡量指标和特征区选择的评价函数,是否存在更能逼真刻画地磁场起伏特征的数学度量,以及如何在特征区内进行基于地磁匹配特征的航迹规划将是作者下一步的研究方向。

[1] Rice H,Kelmenson S,Mendelsonhn L.Geophysical Navigation technologies and Applications[C].Position Location and Navigation Sympo-sium,California,USA,April 26-29,2004.

[2] 张金生,王仕成.地磁匹配制导在巡航导弹中制导段应用的可行性分析[C].中国地球物理学会第二十一届学术年会.长春,2005年08月27日.[ZHANG Jin-sheng,WANG Shi-cheng.Analysis of feasibility of geomagnetic matching for cruise missile guidance[C].The 21st Annual Academic Meeting of Chinese Geophysical Society,Changchun,August 27,2005.]

[3] 周军,葛致磊,施桂国,等.地磁导航发展与关键技术[J].宇航学报,2008,29(5):1467-1472.[ZHOU Jun,GE Zhi-lei,SHI Gui-guo,et al.Key technique and development for geomagnetic navigation[J].Journal of Astronautics,2008,29(5):1467-1472.]

[4] 周贤高,李士心,杨建林,等.地磁匹配导航中的特征区域选择[J].中国惯性技术学报,2008,16(6):694-698.[ZHOU Xian-gao,LI Shi-xin,YANG Jian-lin,et al.Selective criteria of characteristic area on geomagnetic map[J].Journal of Chinese Inertial Technology,2008,16(6):694-698.]

[5] Kennedy J,Eberhart R.Particle swarm optimization[C].Proceeding of IEEE International Conference on Neural Networks,Perth,Australia,November 27-December 1,1995.

[6] Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C].Sixth International Symposium on Micro Machineand Human Science,Nagoya,Japan,October 4-6,1995.

[7] 高鹰,谢胜利.免疫粒子群优化算法[J].计算机工程与应用,2004,6:4-6.[GAO Ying,XIE Sheng-li.Particle swarm optimization algorithmswith immunity[J].Computer Engineering and Applications,2004,6:4-6.]

[8] 乔玉坤,王仕成,张琪.地磁匹配特征量的选择[J].地震地磁观测与研究,2007,28(1):42-47.[QIAO Yu-kun,WANG Shicheng,ZHANG Qi.Selection of the characteristic variable of geomagnetism for matching[J].Seismological and Geomagnetic Observation and Research,2007,28(1):42-47.]

[9] Barid CA,Abramson M R.A comparison of several digital map-aided navigation techniques[M].New York:The Institute and Electronics Engineers Inc Press,1984:231-238.