基于轨道动力学的椭圆轨道悬停方法

王功波,孟云鹤,郑 伟,汤国建

(国防科技大学航天与材料工程学院,长沙410073)

0 引 言

“悬停轨道”是指在连续推力作用下,伴随卫星相对于参考卫星在一段时间内相对位置保持不变的轨道。由于相对静止的特点,“悬停轨道”在空间操作任务中具有广阔的应用前景[1-2]。目前针对悬停轨道的研究,都是在参考卫星为圆轨道的前提下展开的。文献[3-4]研究了相对圆轨道参考卫星在径向的正上方或正下方实现悬停的方法。文献[5]拓宽了悬停的概念,利用几何方法研究了相对圆轨道参考卫星在任意位置实现悬停的一般方法。文献[6-7]应用Hill方程对圆参考轨道上悬停伴飞的初始化及构型维持控制方法进行了研究。目前尚未见到参考卫星为椭圆轨道时悬停轨道设计及控制的相关研究。

一般来讲,严格意义上的圆轨道是不存在的,真实的圆轨道由于各种误差和摄动的影响总是存在小偏心率,因此基于理想圆轨道的假设给出的悬停设计方法总是存在一定的误差。椭圆参考轨道的悬停设计方法,不仅秉含了圆轨道的情况,还可以实现对诸如“Molniya”等大椭圆卫星的悬停,相比圆参考轨道具有更广泛的应用。

文章基于动力学原理,从悬停的定义出发,针对椭圆参考轨道推导了实现悬停的一般方法。特别地,令偏心率为零即可得到文献[3]中关于圆参考轨道悬停方法的结论。根据文章提出的设计方法,着重分析了参考卫星为“Molniya”轨道时的情况,得出一些有益的结论。文章提出的方法不仅适用于设计悬停轨道,也可用于椭圆轨道的空间圆或水平圆等编队设计工作。

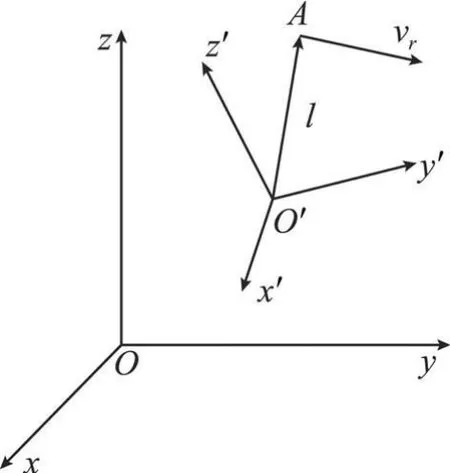
图1 惯性坐标系与动坐标系Fig.1 Inertial Cartesian coordinates and rotating coordinates

1 动力学原理

如图 1 所示 ,o-xyz 表示惯性系,o′-x′y′z′表示动系 。设动系 o′-x′y′z′作一般运动 ,其原点o′的加速度为a′o,角速度为 ω,角加速度为 ε。动点A在动系中的位置矢量为l,速度矢量为v r,根据动力学原理,A在惯性系中的加速度a可表示为

2 悬停方法设计原理

记参考卫星为S,伴随卫星为C,参考卫星的轨道坐标系s-xyz与地心惯性系OE-XYZ的关系如图2所示。

轨道坐标系的x轴与地心矢量重合,并由地心指向参考卫星;y轴在参考卫星的轨道平面内垂直于x轴并指向速度方向为正;z轴由右手定则确定,与轨道面法向重合。r s、r c分别表示参考星和伴随卫星的位置矢量,伴随卫星相对参考卫星的位置矢量为 l。则有

设 rs及l在轨道坐标系的表示形式为rs=(rs0 0)T、l=(x y z)T,则伴随卫星的位置矢量r c可表示为r c=(rs+x y z)T。根据悬停的定义可知,伴随卫星在参考卫星轨道坐标系中的相对速度以及相对加速度均为零,即

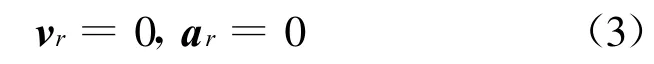
将式(3)代入式(1)可得

其中,ω为参考星轨道坐标系的转动角速度,ε为参考星轨道坐标系的转动角加速度。ω、ε在轨道坐标系中可表示为

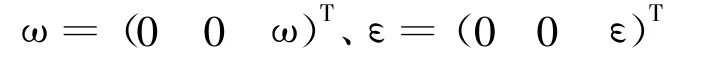
设参考星和伴随星的重力加速度矢量分别为gs、gc,在参考星轨道坐标系内可表示为

记参考星与伴随星的重力加速度矢量之差为 Δg,即 Δg=gs-gc。则有

则维持悬停构型需要的持续控制加速度 acontrol,可写为

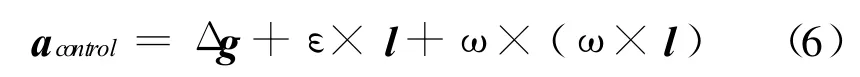
根据卫星轨道理论可知gs=μ/r2s,gc=μ/r2c,其中μ为地球引力常数[8]。则有

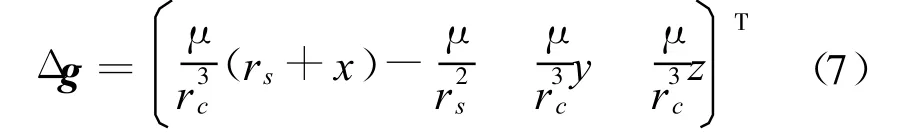
将式(8)代入式(7),并进一步简化可得控制加速度acontrol

3 速度增量计算方法

设参考星六个轨道要素为

其中,a为轨道半长轴,e为偏心率,i为轨道倾角,Ω为升交点赤经,w为近地点幅角,f为真近点角。注意,近地点幅角w与角速度ω的区别。由卫星轨道理论知,参考星轨道坐标系的旋转角速度 ω为

将式(10)、(11)代入式(9),可得控制加速度 acontrol的表达式为

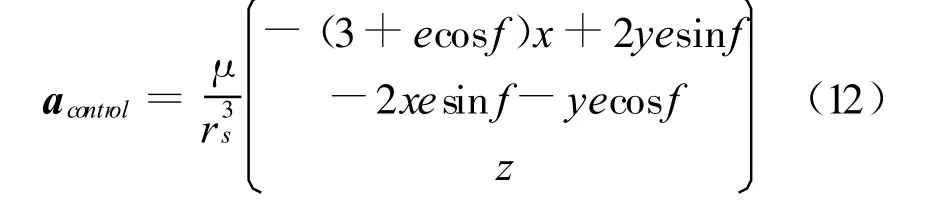
3.1 a control函数的零点

设acontrol=(acxacyacz)T,要对式(13)进行计算,必须首先求式(12)中acontrol三个分量函数的零点。设y=kx,则式(12)可写成

由式(14)知,acx存在零点的充要条件为

即

由式(14)知,acy存在两个零点,记为 f =θy1、f=θy2,可表示为

3.2 a control函数的积分

根据式(10)可得

则一个轨道周期内x方向的速度增量ΔvTx可表示为

如果式(16)不成立,则acx在一个周期内方向始终不发生变化,ΔvTx可表示为

同理可得一个轨道周期内y方向的速度增量 ΔvTy

一个轨道周期内z方向的速度增量ΔvTz为

速度增量 ΔvT可表示为

3.3 速度增量计算公式

下面推导速度增量 ΔvT的具体表达式。由式(14)知,式(13)可分为三个函数的积分,分别为

将式(19)代入式(12)可得

其中,c为积分常数。

如果式(16)成立,即acx存在零点,则将式(26)、(27)、(28)代入式(14)可得 acx的积分表达式为

将式(29)代入式(20),即可得到acx存在零点情况下x方向的速度增量。

如果式(16)不成立,即acx不存在零点,表明x方向的推力在一个轨道周期内方向不会发生变化,根据式(21)和(29)可得

同理,可得acy的积分表达式为

将式(31)代入式(22),即可得到y方向的速度增量。

同理,acz的积分表达式为

在一个轨道周期内的速度增量 ΔvTz为

将式(30)、(32)、(34)代入式(24),即可得到一个轨道周期内总的速度增量 ΔvT。

需要特别指出的是:若x=0,且y≠0,则y=kx不再成立。此时 x轴及y轴方向的速度增量分别为

3.4 e≠0与e=0时几点不同结论

根据控制加速度式(12)以及上述速度增量的表达式可以得出,参考轨道为椭圆轨道相比参考轨道为圆轨道时有几点显著不同的结论。

(1)悬停的相对位置仅在径向(x轴)有分量时,即所谓“悬挂伴飞”,圆参考轨道的控制加速度在轨道坐标系内为常值。椭圆参考轨道的控制加速度是关于偏心率和真近点角的函数,且在近地点和远地点处取得极值。

(2)悬停的相对位置仅在 y轴方向有分量时,圆参考轨道的控制加速度为零。这是因为两星轨道角速度近似相同,不需要控制就可以实现悬停。此时,椭圆参考轨道的控制加速度在 x轴及y轴两个方向都存在分量,且是关于真近点角的函数。在近地点和远地点x轴方向加速度为零,f=±90°时y轴方向加速度为零。

(3)在半长轴及悬停位置矢量相同的情况下,偏心率为零即圆参考轨道上的悬停伴飞需要的燃料是最少的,且燃耗随着偏心率的增大而增加。

4 算例

设参考卫星为“Molniya”,其轨道根数如表1所示。

表1中,长半轴单位为千米,角度单位为度。设伴随卫星在参考星径向正下方实现“悬挂伴飞”,相对距离为1 km,即 l=(-1000 0 0)T。根据式(12)可得控制加速度关于真近点角f的函数表达式

表1 参考卫星初始轨道根数Table 1 Initial orbit elements of chief satellite

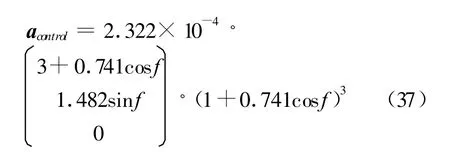
图3给出了一个轨道周期内,加速度随真近点角的变化曲线。从图及(37)式可以看出,总加速度在远地点处取得极小值,约为9.11×10-6m/s2。

图3 一个轨道周期内的加速度变化曲线Fig.3 Relationship between acceleration and true anomaly

图4 速度增量与参考星长半轴的变化关系(e=0.741)Fig.4 Relationship between velocity increment and semi-major axis

根据式(30)、(32)、(34)可得,一个轨道周期内三个坐标轴方向的速度增量分别为 ΔvTx=9.915 m/s、ΔvTy=2.857 m/s以及 ΔvTz=0,总的速度增量大小为 ΔvT=10.317 m/s。在偏心率保持不变的条件下,改变参考卫星的长半轴,得到维持上述构型所需速度增量与参考星轨道长半轴的变化曲线,如图4所示。

同理,固定长半轴,速度增量与偏心率的关系如图5所示。由图5可以看出,在长半轴相同的条件下:所需速度增量随偏心率的增加而增大,e=0即参考卫星运行在圆轨道上时,所需速度增量最小;偏心率较小时,对速度增量的影响并不显著;偏心率较大时,速度增量随偏心率的增大而急剧增加。

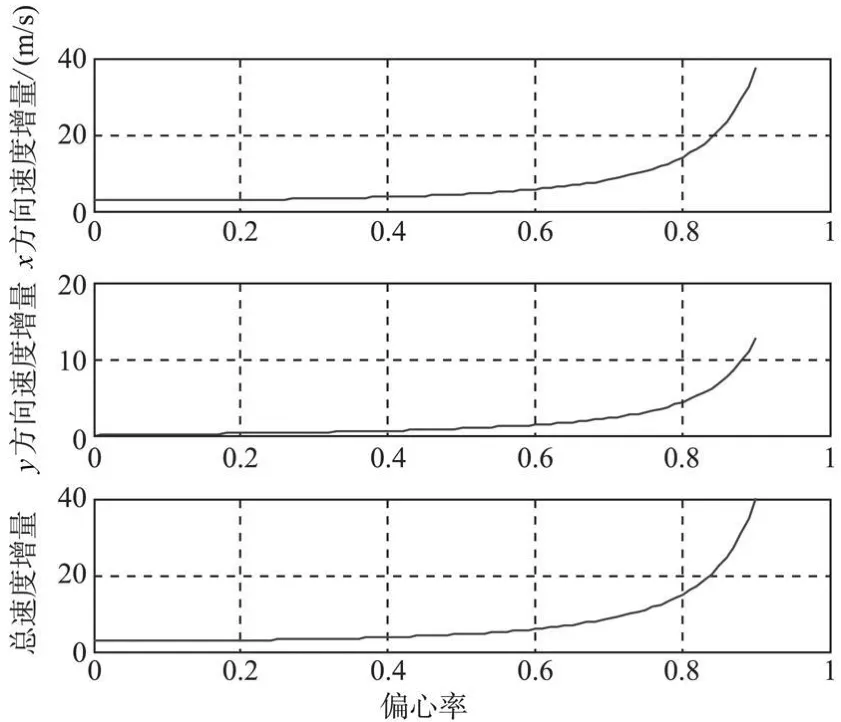
图5 速度增量与偏心率的变化关系(a=26553.375 km)Fig.5 Relationship between velocity increment and ecctricity

设伴随星在参考星轨道坐标系的方位角为 α ,高度角为β,取值范围分别为α∈[0,2π]、β∈[-1/2π,1/2π]。则伴随星的位置矢量可写成 l=l(sinβ cosβsinα cosβcosα)T。在相对距离不变的情况下,在不同位置实现悬停所需的速度增量如图6所示。

图6 一个轨道周期内速度增量在不同位置的等高线示意图(a=26553.375 km,e=0.741,l=1 km)Fig.6 Velocity increment contour line during a orbital period

由图6可以看出,速度增量受方位角的影响较小,而对高度角比较敏感,当伴随卫星处于参考星正上方或正下方时速度增量取到最大值。

5 误差分析

以上结论都是在已知参考卫星轨道的条件下得出的,实际上,参考卫星的轨道总会存在一定的定轨误差。因此,本节着重分析这些定轨误差对悬停轨道设计的影响。

控制加速度acontrol可以写成如下形式

则,定轨误差对控制加速度的影响为

下面针对上节的悬停算例,定量分析各参数对推力的影响。

地心距r

将式(12)代入式(39),仅考虑径向定轨误差,并忽略高阶小量,可得

考虑“Molniya”卫星近地点径向定轨精度100 m,代入上式可得d ac/ac＜4.3×10-5。

偏心率e

仅考虑偏心率定轨误差

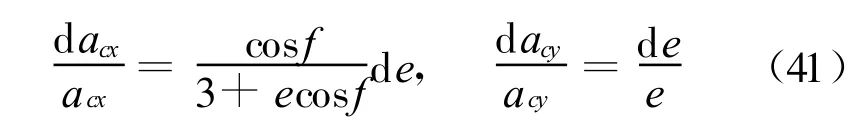
考虑偏心率定轨精度10-5,上式在远地点取得最大值,代入数值可得d ac/ac＜1.4×10-5。

真近点角f

同理,仅考虑真近点角误差,并假设真近点角定轨精度为10-5弧度,代入数值可计算得到:d ac/ac＜0.83×10-5

综上所述,在径向100 m、其它轨道根数10-5定轨精度条件下,由于定轨误差引起的悬停推力偏差不足标准推力的万分之一。

6 结束语

文章从悬停轨道的定义出发,基于动力学原理,推导了针对任意类型参考轨道实现悬停的方法,突破了目前参考卫星仅局限于圆轨道的限制。进一步推导了一个轨道周期内维持悬停需要的速度增量计算公式。以“Molniya”轨道为例,计算了实现“悬挂伴飞”需要的推力及速度增量,分析了速度增量与轨道高度、偏心率的关系,给出了燃料消耗与悬停相对位置的等高线视图。最后定量分析了参考轨道定轨误差对控制加速度的影响。文章提出的方法也可用于椭圆轨道的空间圆或水平圆等非自然编队构型设计。

[1] 袁建平,朱战霞.空间操作与非开普勒运动[J].宇航学报,2009,30(1):42-46.[YUAN Jian-ping,ZHUZhan-xia.Space operations and non-keplerian orbit motion[J].Journal of Astronautic,2009,30(1):42-46.]

[2] 王萍,袁建平,范剑峰.关于非开普勒轨道的讨论[J].宇航学报,2009,30(1):37-41.[WANGPing,YUANJian-ping,FAN Jianfeng.Discussion on non-keplerian orbit[J].Journal of Astronautic,2009,30(1):37-41.]

[3] 林来兴,黎康.卫星对空间目标悬停的轨道动力学与控制方法研究[J].中国空间科学技术,2008,28(2):9-12.[LIN Lai-xing,LIKang.Orbit dynamics and control of satellites hovering over space target[J].Chinese Space Science and Technology,2008,28(2):9-12.]

[4] Broschart S B,Scheeres D J.Control of hovering spacecraft near small bodies:Application to asteroid 25143 Itokawa[J].Journal of Guidance,Control and Dynamics,2005,28(2):343-354.

[5] 闫野.卫星相对空间目标任意位置悬停的方法研究[J].中国空间科学技术,2009,29(1):1-5.[YAN Ye.Study of hovering method at any selected position to space target[J].Chinese Space Science and Technology,2009,29(1):1-5.]

[6] Sawai S,Scheeres D J,Broschart S B.Control of hovering spacecraft using altimetry[J].Journal of Guidance,Control and Dynamics,2002,25(4):786-795.

[7] 李元凯,敬忠良,胡士强.连续有限推力下园轨道目标相对动力学悬停控制[C]//空间非开普勒轨道动力学与控制专题研讨会会议论文集.哈尔滨:哈尔滨工业大学出版社,2008:362-369.[LI Yuan-kai,JING Zhong-liang,HU Shi-qiang.Circle orbit hovering control based on continuous finite thrust[C]//The Volume of Space Non-Keplerian Orbit Dynamicsand Control Conference.Harbin:Harbin Institute of Technology Press,2008:362-369.]

[8] 刘林.航天器轨道理论[M].第1版.北京:国防工业出版社,2000.[LIU Lin.Orbit theory of spacecraft[M].First Edition.Beijing:Defense Industry Press,2000.]