高斯光束经多组元变焦扩束系统变换

谢先闻

(浙江外国语学院理工学院,浙江杭州310012)

1 引 言

激光扩束器系统通过压缩激光束的空间发散角,使输出的激光束满足要求,已被广泛应用于诸如傅立叶频谱变换光学、空间滤波、全息照相、激光测距、雷达跟踪系统等领域.

常规的激光扩束器使用的是具有确定倍率的望远镜倒置系统,但近年来变焦扩束系统由于具有可变的扩束倍率,在满足发散角和光束宽度的前提下,使系统的扩束比具有可调性,而得到更广泛的应用.因此分析高斯光束经该类变焦扩束系统的规律无疑具有实际的意义.

文献[1-2]采用几何光学的方法分析了三组元系统的变焦规律,但一个实际系统对高斯光束的变换用几何光学的方法分析毕竟与实际是有区别的,其传输时的规律不同于几何光束,通过透镜时的变换规律也与几何光束不同,因此需要按照高斯光束特有的传播变换规律对变焦扩束系统进行分析;而从实际应用的角度来看,有时需要寻找在扩束系统用几何光束代替高斯光束的条件,以方便设计;同时一个变焦扩束系统又可以有各种组合方式,如常见的由变焦组和固定组实现变焦功能时,有正-负透镜组合、负-正透镜组合等,有固定组在前以及固定组在变焦组之后;另外,由于要求校正各种轴上和轴外的像差,有时需要使用多片透镜组合.

为了适应这些普遍的情况以及由非常规元件(如梯度折射率透镜)构成的系统分析的需要,本文采用矩阵光学方法,研究高斯光束经一般的变焦扩束系统的变换规律,在重焦与离焦的情况下导出了用系统的矩阵元表示的经过该扩束系统后的束腰宽度、出射光腰位置等计算公式.作为应用例,利用导出的解析公式,详细讨论了一个三组元的变焦扩束系统对高斯光束的变换,考虑了各参量变化对输出高斯光束束腰宽度和位置的影响,给出了数值计算结果.

2 多组元变焦扩束系统对高斯光束的变换

2.1 多组元变焦扩束系统的基本结构和扩束原理

一个变焦扩束系统一般可以看作是由变焦和补偿两部分构成的,而变焦部分往往又是含有变焦组和固定组,如图1所示.从几何光学来看,变焦部分的共同作用是产生系统焦距的改变:当其中的变焦组相对于固定组连续移动时,它们的组合焦距就连续改变,产生新的焦点;而补偿部分设计成可移动的,当变焦部分移动时,补偿部分也做相应的移动,使其前焦点稳定在变焦部分的输出上,组合成新的扩束比的扩束系统.

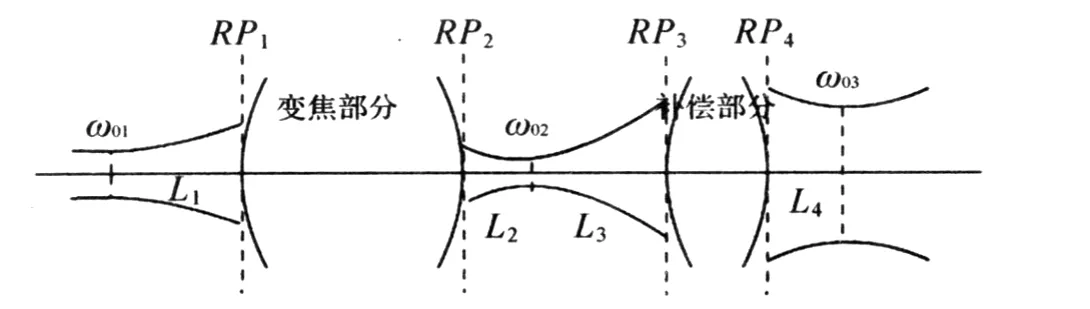
图1 变焦扩束系统结构示意图

从高斯光束的变换来看,束腰宽度为ω01的入射高斯光束,经过变焦部分变换的出射光腰(整个系统的中间光腰)束腰宽度为ω02,再经补偿部分后出射,得最后出射高斯光束的束腰宽度ω03,此ω03与入射高斯光束束腰宽度ω01之比,即扩束比为

对于扩束系统,需要ω03＞ω01,且不同的用途需要不同的扩束比.按照束腰宽度、远场发散角之间的关扩束的结果减少了出射光束的远场发散角.式中θ01、θ03分别是入射和出射高斯光束的远场发散角.

2.2 多组元变焦扩束系统的高斯光束变换

分析基模高斯光束变换的出发点是ABCD定律[3],将它应用于给定的系统,则有[4]

和

式中ω0、ω0′分别为该系统入射和出射光腰的束腰宽入射光束的瑞利长度(或者称共焦参数);A、B、C、D为所考虑的系统的入射和出射光腰之间系统的光线变换矩阵元.由(2)(3)两式分别应用于变焦部分和补偿部分,可以得出高斯光束变换的规律.

2.2.1 变焦部分的分析

图1中变焦部分的第一个界面和最后一个界面分别为RP1、RP2,以此RP1、RP2为参考面的光线变换矩阵为入射光腰到中间光腰之间的光线变换矩阵可以由矩阵光学方法得出:

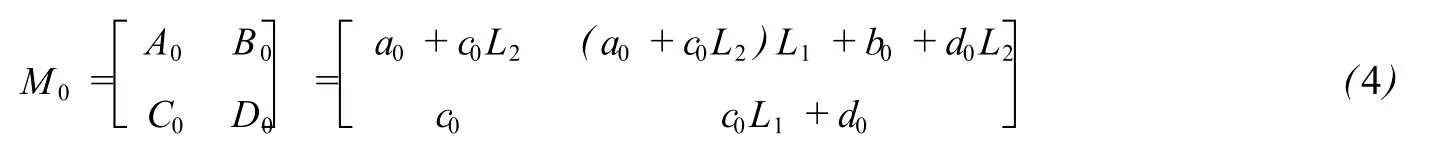
L1是入射光腰到参考面RP1之间的距离,L2是参考面RP2到中间光腰之间的距离.与一般高斯光束变换的文献中采用相同的符号规约,即物方量以RP1为参考面,逆入射光方向量取为正,像方量以RP2为参考面,顺入射光方向量取为正.

将(4)中的相关矩阵元代入(2)(3),可得:

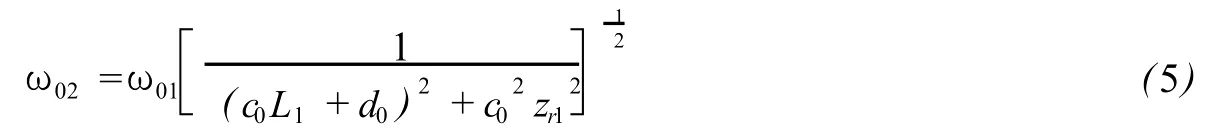
以及

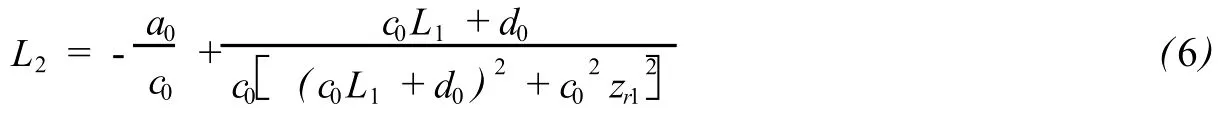
2.2.2 补偿部分的分析

如前所述,在变焦部分改变倍率的过程中,中间光腰的位置不断地改变,补偿部分要同步地移动,使其前焦点处在中间光腰处,把此情况称为重焦,此时补偿部分为傅立叶变换系统,这是为了获得大的扩束效果所需要.但补偿部分在移动过程中,由于调节的误差,变焦部分输出的位置并不能始终稳定在补偿部分的前焦点上,即有轴向的失调,可称此情况为离焦.以下就重焦和离焦的情况分开进行讨论.

2.2.2 .1 重焦情况下的分析

设补偿部分的入射光腰ω02到其第1参考面RP3的距离为L3,经过补偿部分出射的光腰ω03在其第2参考面RP4后L4处,这前后两参考面之间的光线变换矩阵到ω03之间系统的光线变换矩阵可以写为

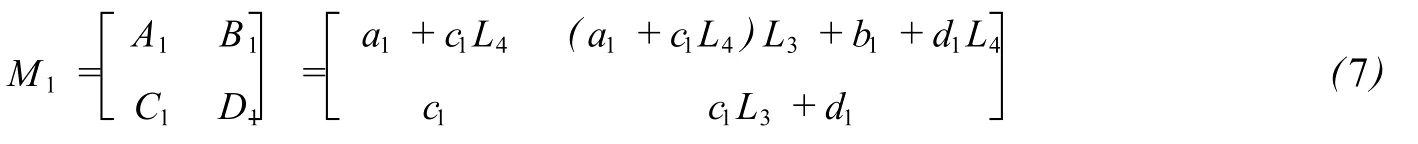
由补偿部分的的作用来看,要成为傅立叶变换系统,则要A1=0,D1=0,由此得:

这正是补偿部分以RP3为参考面的物方焦距(物方焦截距)和以RP4为参考面的像方焦距(像方焦截距).由此可得RP2与RP3之间的距离为:

而在A1=0,D1=0情况下,由(2)可有:

即ω03反比于ω02,要增大ω03,需要尽可能地减少ω02,因此为要得到尽可能大的扩束效果,要求变焦部分起聚焦作用,(6)式代入上式,则得整个系统的出射光腰束腰宽度与入射光腰束腰宽度之比,即扩束比:

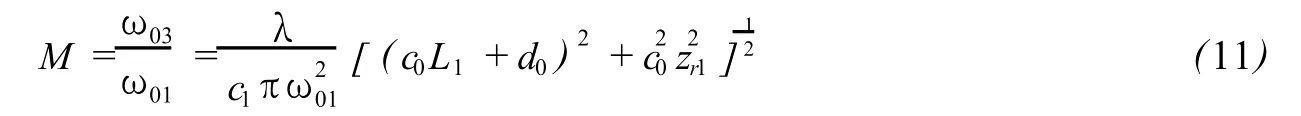
同样,若把入射高斯光束光腰到出射光腰的变换,看做是物-像变换,可令整个系统的矩阵元B=0,可得系统的横向放大率

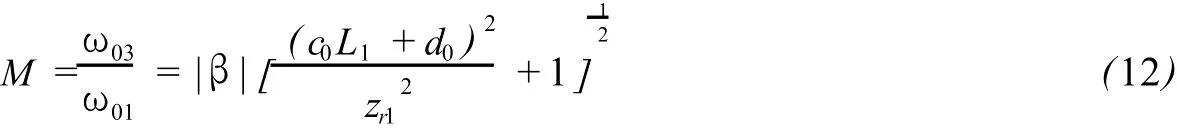
2.2.2 .2 离焦情况下的分析

在轴向失调时,ω02与RP3的距离不再是有一个失调量,记为Δ,则ω与RP023的距离时从中间光腰ω02到最后的出射光腰之间的光线矩阵:

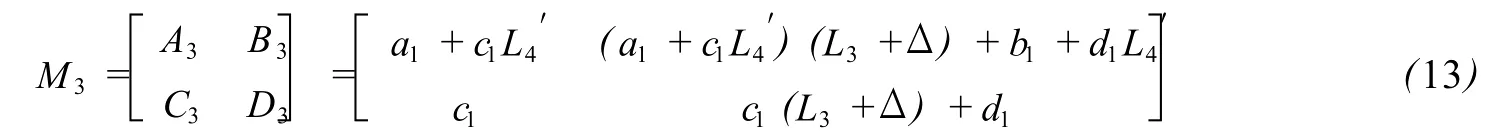
将(13)式中的有关矩阵元代入(2)(3)式,可得扩束比

以上所导出的所有公式正是反映了高斯光束经过可变焦扩束系统的变换规律.从导出的公式,可以看出几何光束与高斯光束的明显区别,例如由(5)(12)式可见,由于zr1的存在,变焦部分的聚焦比M1必小于变焦部分的几何放大率A0,扩束比M必大于整个系统的放大率β.几何光学的规律仅在一定的条件下适用,例如由(5)式可见,在(c0L1+d0)≫zr1时,M1≈A0,由(12)式可见,当zr1≫(c0L1+d0)的时候,扩束比M≈β.

由以上导出的公式也可见,中间束腰宽度ω02和位置L2,系统重焦和离焦时的输出ω03和,以及L4′等与入射光腰的位置L1、入射束腰宽度ω01以及与系统参量(矩阵元)均有关,此系统参量由系统的具体组态决定.作为应用例,我们结合一个具体的三组元变焦扩束系统来讨论这些输出量的变换规律.

3 应用例

3.1 三组元变焦扩束系统

以文献[1]所介绍的三组元变焦扩束系统为例,如图2所示.

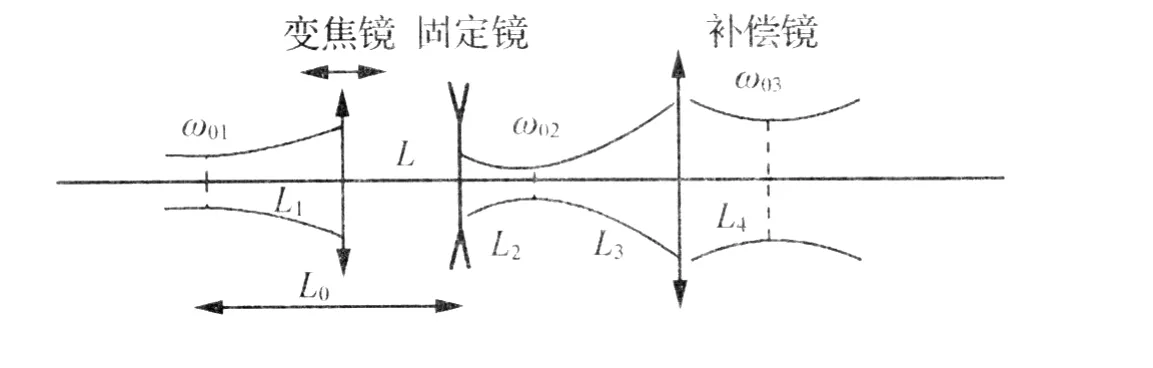
图2 三组元变焦扩束系统

图中变焦透镜(焦距f1)与固定镜(焦距f2)(这些焦距均表示像方焦距,以下同)构成了变焦系统,当变焦镜相对于固定镜移动时,该两透镜系统的组合焦距即发生改变.该变焦系统的光线变换矩阵

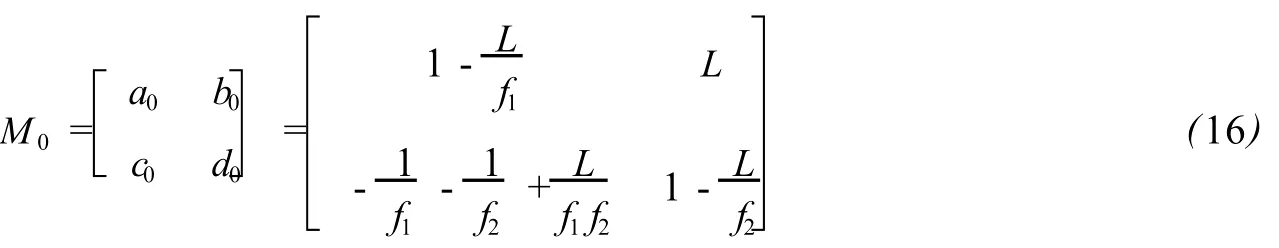
对于补偿镜,其光线矩阵可以表示为

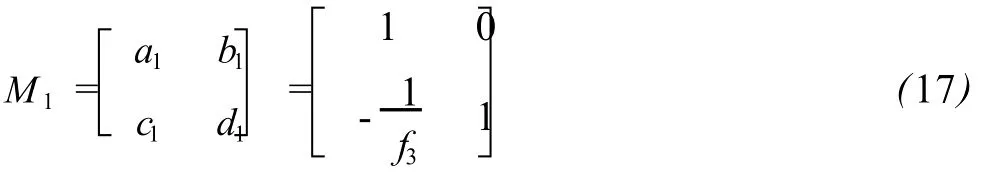
是:对于变焦扩束系统由于两镜之间的距离L是变化的,因此入射光腰不能保持在变焦部分的前焦点处,即不可能保

把(16)(17)中的矩阵元代入前面得出的所有公式,且选固定镜为参考位置,则L1=L0-L,可以得到在现在的组态情况下这些公式的具体形式.限于篇幅,在以下讨论中仅列出少数必要的几个.

3.2 数值计算和讨论

在图2的组态情况下,设f1＞0,f2＜0,f1＞|f2|,有三段可以产生连续的变焦效果的区域:(1)0＜L＜f1+f2,(2)f1+f2＜L＜f1和(3)L＞f1.以下就利用区域(1)为例,以文献[1]给出的参数来讨论.取f1=15mm,f2=-5mm,f3=200mm,则区域(1)的变焦范围为0＜L＜10mm.取λ=0.6328×10-3mm.

由(5)(11)式可见,ω01一定的时候,变焦部分的聚焦比M1随着L1的增大而减小,而M随着L1的增大而变大;当L1一定(在某个确定的L处,也就是L0一定)的时候,M1随着ω01的增大而单调地减小,扩束比M随着ω01的增大而单调地减小;而当L1、ω01以及系统参量同时变化的时候,它们对输出的影响,要比较它们的取值的大小,例如当c0zr1≫c0L1+d0的时候,则M≈即在此情况光束变换特性唯一地由系统的放大率决定.

在图2的组态下,系统在重焦情况下的扩束比和输出光腰位置分别为

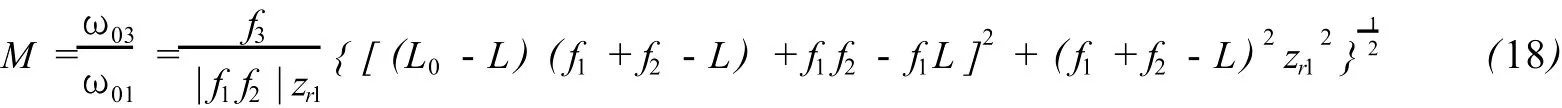
和

即在重焦的情况下,输出光腰的位置即在补偿镜的后焦点处.而整个系统的几何光学横向放大率

图3是根据(18)式在ω01=0.2mm的时候作出的扩束比和几何光学横向放大率β随L变化的图形.由图可见,在相同的入射光腰ω01情况下,入射距离L0越大,扩束比也越大.例如由式(11)或(18)可见,当L1(L0)→时,即入射光腰与变焦组RP1参考面距离无限大的时候,ω02→0,此时ω03以及扩束比M→.但从实际应用来说,必须考虑到实际的需要和受通光孔径的限制,因此入射光腰不能离系统太远[5],应该根据实际的需要选择入射光腰的位置.

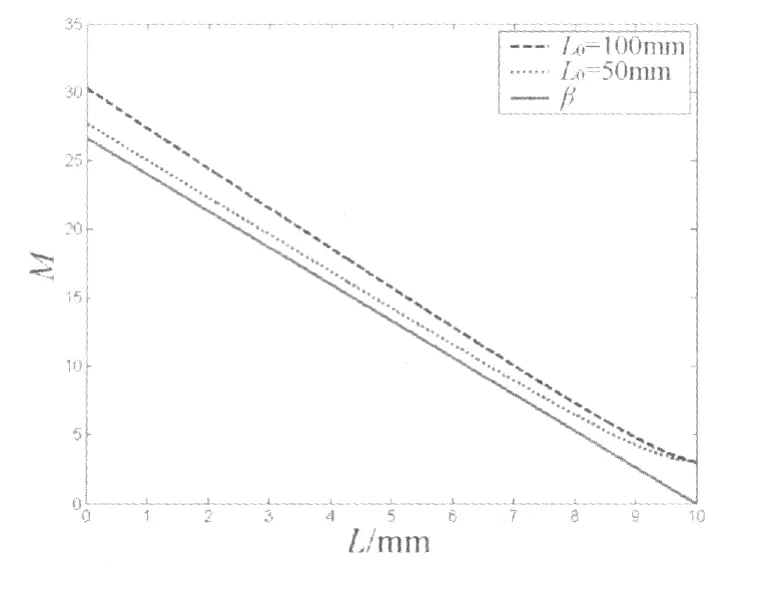
图3 重焦时扩束比M随变焦部分两镜之间的距离L的变化

表1是在入射距离L0=50mm,L=6.25mm,即系统的放大率β=10情况下几种不同入射ω01时对应的扩束比.可见相同的入射距离,入射光腰ω01越大,扩束比越小,越接近于系统的横向放大率β,这些正是前面所讨论的zr1≫c0L1+d0的情况在此组态下的体现.

表1 不同入射束腰宽度时的扩束比

图3中,两条曲线在L=10mm处相交,说明扩束比与L0无关,这可由(18)式得出:在L=10mm时与ω01有关,与L0无关.

图4为中间光腰在当前组态下的位置L2随L变化的曲线,图中L2是相对RP2的距离,其取负值是因为在图2组态中是负焦距.图中曲线1、曲线2对应于L0=50mm,但入射束腰宽度分别为ω01=0.1mm、ω01=0.2mm的情况,而曲线3是当平行光入射时补偿部分的输出位置,也即补偿部分的像方焦距由图可以清楚地看出入射束腰宽度大时,中间光腰的位置变化规律越接近于同样在L0增大,也接近于的变化规律.

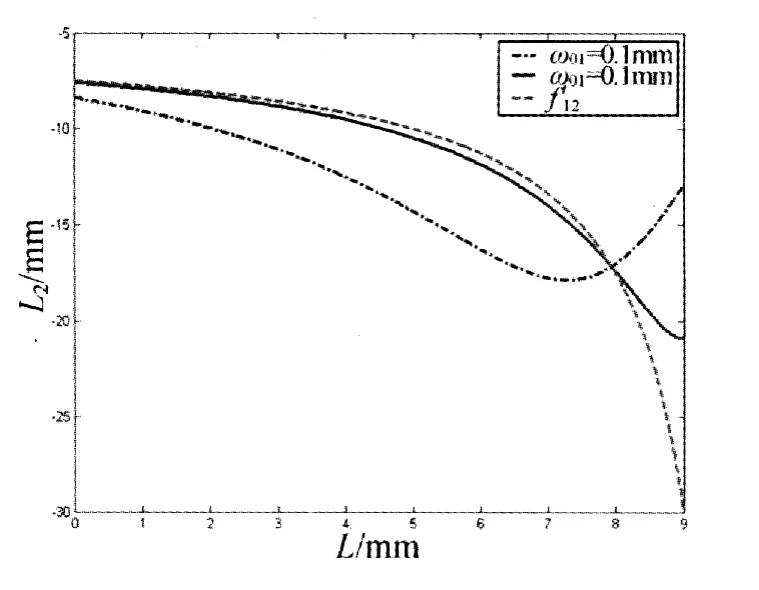
图4 中间光腰的位置随L的变化规律

按照(9)式,L2加上补偿镜的焦距f3即为在重焦时补偿镜移动的规律,实际的变焦扩束系统是采用凸轮结构来主导补偿组的运动,图4的规律以及相关公式可以用于凸轮的设计.

离焦时的扩束比和出射光腰位置由式(14)和(15)可见,也与L0及ω01有关.分析式(15),在现在给定的数据情况下,则式(15)可以近似离焦时的出射光腰位置已经远离补偿镜的后焦点了;分析(14)式,可知:在确定的L、L0及ω01,也就是ω02确定的情况下,离焦时的扩束比随着Δ的增大而迅速地减小,且与Δ的正负无关.为节省篇幅起见,以上两图略.

图5是在给定ω01、L0时,离焦与重焦时的扩束比随L的变化关系的比较.由图可见,在相同L处扩束比随着离焦量Δ的增大而迅速地减小,扩束比的迅速下降,意味着远场发散角的增大;而离焦情况下的扩束比随着L的增大而接近于重焦时的扩束比.

图6是在相同ω01、L和给定离焦量时,离焦与重焦情况下扩束比随L0的变化规律的对比,与重焦情况不同的是:随L0的增大,扩束比反而是减小的.

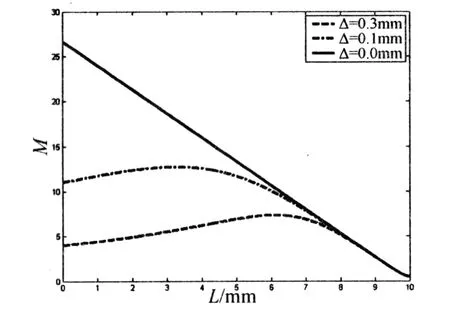
图5 ω01=0.5mm时离焦与重焦的扩束比的比较

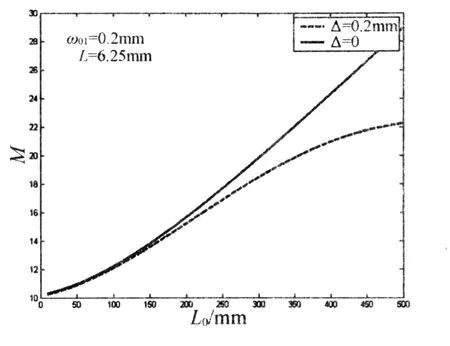
图6 离焦与重焦扩束比随L0的 变化规律的对比

4 结 语

本文所导出的公式反映了高斯光束经多组元变焦扩束系统变换规律.由于光线矩阵方法的普适性,这些公式也具有普适性.

研究结果表明:变焦扩束系统输出束腰宽度、光腰位置、补偿镜移动规律等与入射光腰位置、入射束腰宽度以及系统参量均有关,它们之间的关系由本文所导出的一系列公式给出.在进行变焦扩束系统设计时要根据实际需要综合地考虑这些因素.如入射光腰距离系统较远的话,虽然可以提高扩束比,但对于光学元件的口径以及系统的工作距离等提出了要求;入射束腰宽度的变化极大地影响系统的扩束比,而如入射束腰宽度较大的话,虽然更接近于几何光学的情况,有助于简化对规律的分析,但中间光腰的宽度太小,导致能量过分集中,有可能出现空气的击穿现象,以致光学元件受到损伤.

此外,在设计的时候要根据所需要的系统扩束比来综合地考虑变焦的范围,还需要考虑像差、以及所用元件的优化问题.

[1] 孔祥蕾,郝沛明.变焦扩束系统的光学设计[J].应用光学,2001,22(5):7-11.

[2] 蔡长达.变焦距激光扩束系统的结构设计[J].激光与红外,1996,21(1):30-31.

[3] Kogelnik H. Imaging of optical mode-resonators with internal lenses[J].Bell Syst Tech J,1965,44(3):455-494.

[4] 王绍民,赵道木.矩阵光学原理[M].杭州:杭州大学出版社,1994:41-50.

[5] 程洁.激光扩束望远镜的失调与扩束比[J].激光技术,1995(2):57-60.