基于叶溪河大桥的配索方案对比研究

舒 彬

(陕西铁路工程职业技术学院,陕西渭南 714000)

1 概述

预应力混凝土连续箱梁桥常见的配索方式有两种：一种是采用曲线预应力筋,布置下弯索,由下弯索提供抗剪能力；另一种是取消下弯索,采用直线预应力和竖向预应力共同抗剪。第一种布索方式,优点是下弯索与梁体斜向主拉应力方向一致,抵抗主拉应力的效果很好,缺点是预应力筋要从顶板横向弯曲到腹板对应的位置,再下弯,摩阻损失大,弯曲索法向会产生一定的拉应力,且很难锚固到截面边缘,一般只能锚固到腹板侧面专门设置的齿板上,对腹板横向变形和局部应力都有一定不利的影响。第二种布索方式主要依靠竖向纵向直线预应力组合抵抗主拉应力；通过调整竖向预应力的大小,在理论上是可以完全克服主拉应力的,受力简单,用钢量少且施工方便[1]；然而20世纪90年代以来采用这种方式的连续梁在腹板上出现了大量的斜裂缝[2],说明这种配索方式也存在缺陷。基于叶溪河大桥实测和分析,对比两种配索方案的预应力损失对内力的影响,综合分析并提出合理的配索方式。

2 直线+竖向配索方案的理论分析

根据箱梁优化理论可知[1]：腹板的主拉应力可以通过竖向预应力和纵向预应力两者组合来控制,而不需要下弯预应力索来承受。主拉应力公式

假设主拉应力σl≤0(即没有拉应力或表现为主压应力)则

即σxσy≥τ2

当σxσy≥τ2时，腹板只出现主压应力或既没有主拉应力也没有主压应力；采用直线配索方式,由于预应力索没有弯曲,法向不会出现混凝土拉应力,故不需要布置单独的钢筋抵消弯曲预应力产生的法向拉应力,受力模式简单,用钢量少,施工方便；理论上完全可以取消下弯预应力索和弯起预应力索,只要调整σxσy的乘积就可以了。

3 竖向预应力的有效性调查和分析

宜昌—万县叶溪河大桥主体结构为80 m+108 m+80 m连续箱梁铁路桥,竖向预应力筋采用精轧螺纹粗钢筋；对叶溪河大桥中跨1/4跨附近的竖向预应力损失监测报告中根据测试数据建立指数拟合竖向预应力损失曲线如图1所示。

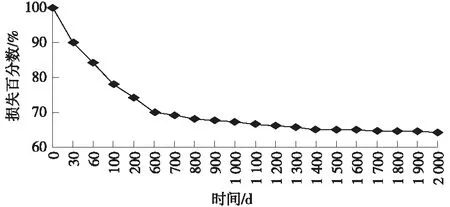
图1 指数拟合预应力损失曲线

由图1可以看出：锚固完成后的一个月左右损失最快可达10%,两年内损失在25%～30%；两年以后损失逐渐减慢,从损失拟合曲线推算,大概5～6年预应力损失就可达到或超过50%。假设先按纵向直线配筋方式分析,且直线预应力损失不计,将测试数据等代转换为混凝土的竖向压应力后带入主拉应力公式计算；全桥有限元分析模型如图2所示。

图2 有限元模型

表1列出了叶溪河大桥中跨1/4跨附近腹板局部应力状态分析,其中预应力1：直线预应力+80%有效竖向预应力设计值；预应力2：直线预应力+60%有效竖向预应力设计值；预应力3：直线预应力+30%有效竖向预应力设计值。

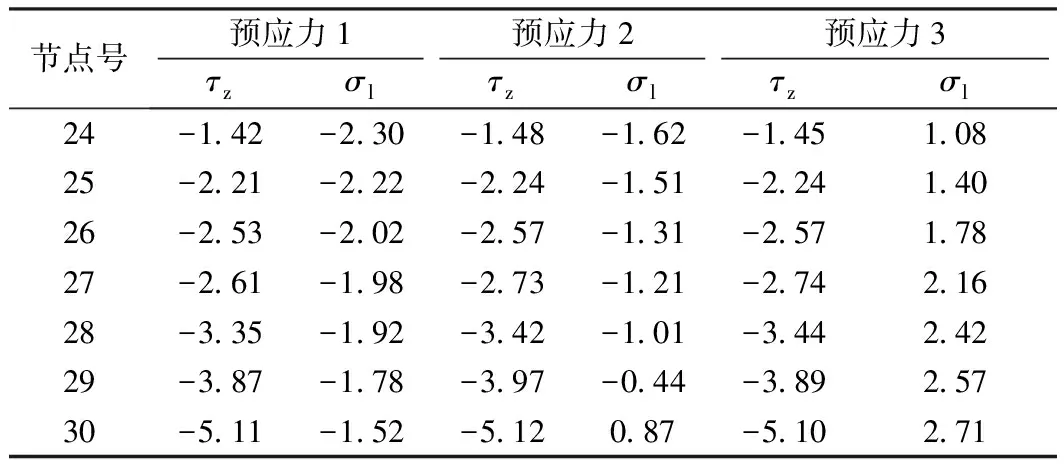
表1 1/4跨附近箱梁腹板在不同竖向预应力条件下的主应力 MPa

注：τz为沿纵断面方向的空间剪应力；σl为沿纵断面方向的主拉应力。

由表1可以看出：竖向预应力按80%设计值计算时,1/4跨基本为主压应力,没有主拉应力出现；竖向预应力按60%设计值计算时,1/4跨就开始出现拉应力；竖向预应力按30%设计值计算时,1/4跨附近主压应力基本全部转换为主拉应力,在30号梁段最大值高达2.71 MPa。从上述分析及文献[3]中可知,理论上竖向预应力对减小主拉应力贡献很大。但是对于梁高较小,竖向预应力筋较短,当预应力粗钢筋锚固端稍有施工不当,或锚固螺栓变形,引起粗钢筋少量的缩短,就会造成很大的预应力损失,所以施工结束后粗短的预应力筋要达到设计值常常很困难,这就造成实际的竖向预应力很小,施工质量较差的结构甚至竖向预应力消失。调查发现，很多结构实际竖向预应力不到设计值的50%,有些梁高2 m左右箱梁,只有设计值的20%～30%[4]。竖向预应力大量损失是很难避免的,这说明主要用竖向预应力来保证斜截面主拉应力的方法是不可靠的。

4 采用曲线式配索

叶溪河大桥采用了下弯曲线预应力索和竖向预应力相结合的配筋方式,为了有足够的安全储备,先不考虑竖向预应力的作用,忽略弯曲索使混凝土产生的法向局部拉应力,按只配纵向曲线预应力方案分析,有限元配索模型如图3所示。

图3 纵向曲线布索模型

4.1 正应力分析

施加预应力后,整体截面正应力组合值从图4可以看出：整体截面基本受压,没有受拉区出现,最大值位于边跨3/4,中跨3/8、5/8左右附近区域,组合最大压应力为10.3 MPa。

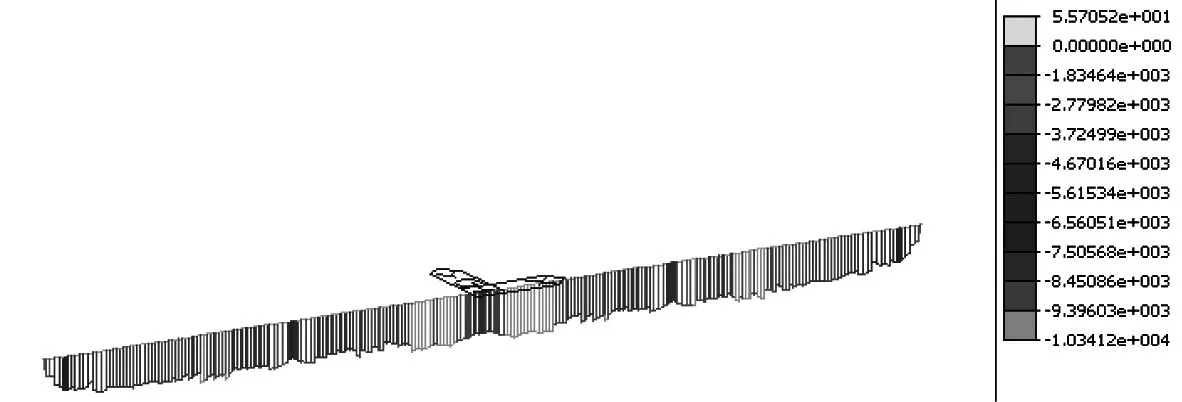
图4 施加预应力后截面实际应力组合值(单位：kPa)

由于纵向预应力筋较长,除了锚具变形、混凝土收缩徐变等前期损失外,后期预应力损失主要表现为混凝土的收缩徐变,预应力筋的应力松弛。这两种预应力损失在后期运营阶段都很小,为了保守起见,按远期预应力损失20%进行截面应力分析。从图5中可以看出组合正应力分布规律基本不变,全梁基本受压,最大值位于边跨3/4,中跨3/8、5/8左右附近区域,组合最大压应力为8.29 MPa。从图6中可以看出,箱梁上下缘也基本整桥受压,边跨支座附近压应力较小,其他部位7.5 MPa左右波动,故箱梁上下缘也不会出现竖向裂缝。C50的混凝土抗压设计值远大于实际应力值,所以从正应力角度出发,这样配置预应力筋是非常合理的。

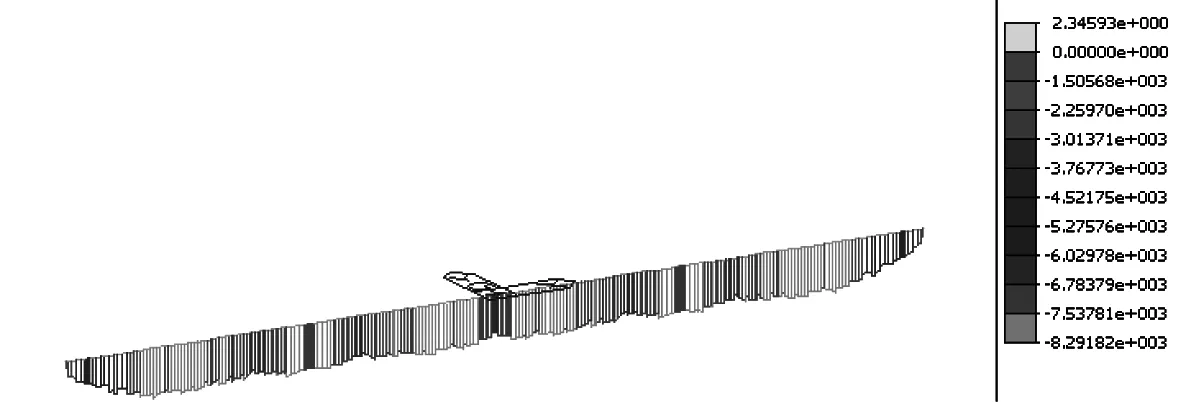
图5 按远期预应力损失20%进行截面应力组合值(单位：kPa)

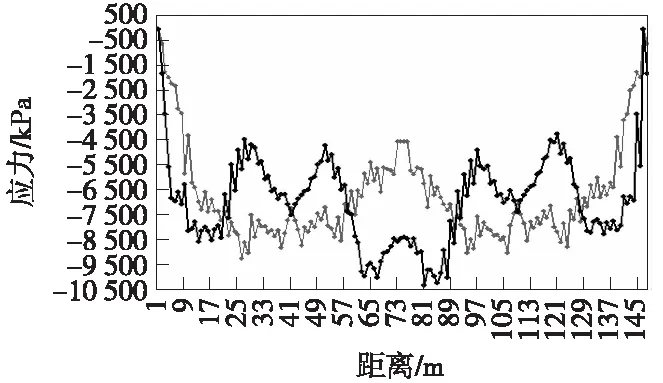
图6 箱梁上下缘正应力值

4.2 剪应力分析

从图7中明显看出，支座处剪应力改变不大,但其他截面剪应力很小,基本被曲线预应力抵消。按曲线预应力损失20%后的剪应力值计算如图8所示,从图8中可以看出,边跨支座附近剪应力变化较大,其他部位剪应力变化幅度很小,均在混凝土的抗剪强度设计值范围之内。所以除了还需要加强支座应力调整外,只要预应力损失不大,这种曲线预应力配筋方式对抵消剪应力也是有效的。

图7 实际截面剪应力值(单位：kPa)

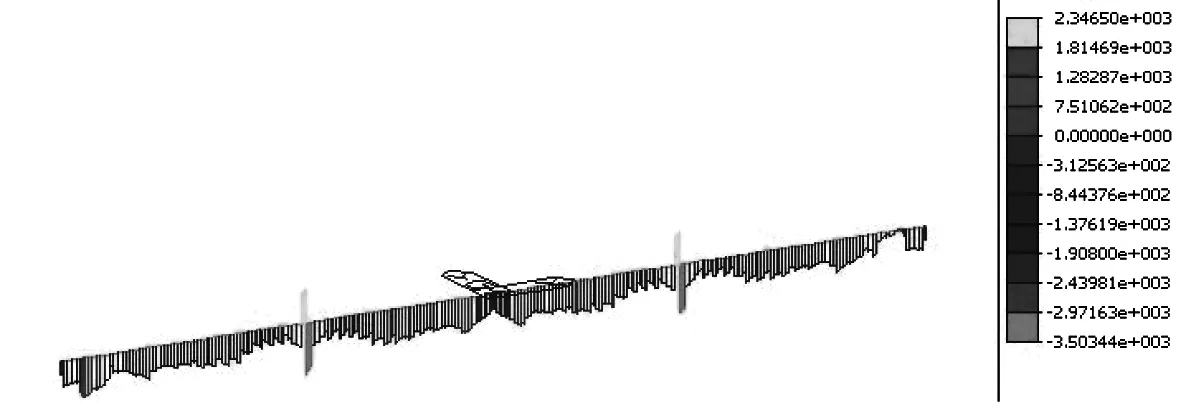
图8 曲线预应力损失20%后的剪应力值(单位：kPa)

4.3 斜截面主拉应力分析

以上分析可以看出,全桥混凝土基本上是整体受压,没有出现拉应力区(即σx≤0),剪应力除支座外也被抵消到很小范围内。假设竖向预应力全部损失(即σy=0),由主拉应力公式得

斜截面的主拉应力基本被抵消并转化为主压应力,叶溪河大桥即使在竖向预应力有一定损失的情况下也没有产生斜裂缝,箱梁下上缘也没有竖向弯曲裂缝出现,这说明采用纵向曲线预应力配筋方式是合理的。

5 分析与结论

通过对两种配索方式分析可以看出：直线+竖向预应力配索方式,在竖向预应力损失小于50%时,腹板斜截面一般不会出现主拉应力裂缝,此时这种配索方式总体上优于下弯配索方式；但竖向预应力在长期作用下,预应力损失很难保证在50%以内,大部分都在5～6年以后突破此损失值,使截面转为主拉应力区而开裂。下弯配索方式管道摩阻力大,前期预应力损失较大,但可以通过适当超张拉加以弥补,后期预应力损失较小,叶溪河大桥即使按20%预应力损失计算,斜截面正截面均基本全桥受压,从计算角度不会出现弯剪裂缝和弯曲裂缝；箱梁顶板底板弯曲索法向混凝土会局部受拉,通过配置一定的构造钢筋可以弥补这一缺陷[5],从实际观测也没发现横向弯曲索附近有纵向裂缝,腹板下弯法向受拉完全被纵向压应力抵消,基本可以不考虑。通过分析计算，曲线配索式加合理的构造钢筋布置是可以避免长期服役状态下裂缝的出现。

从叶溪河大桥实测分析可以得到以下主要结论。

(1)在理论上取消下弯索,通过适当调整顶、底板索和竖向预应力筋,调整截面σxσy的乘积,采用纵向预应力和竖向预应力联合抵抗构件斜截面主拉应力的方式,来实现对腹板裂缝控制是可行的,不仅减少了钢材的用量,且施工简单。

(2)实际上用精轧螺纹粗钢筋做成的竖向预应力筋预应力损失较大,且很难控制；由于竖向预应力的有效性不可靠,导致纵向直线预应力抵抗主拉应力的效果也大打折扣,结构分析模型与真实情况差异过大,实际结构很容易出现主拉应力而导致腹板斜裂缝。

(3)采用主要以纵向曲线预应力索来抵抗斜截面主拉应力,以竖向预应力作为安全储备而不参加计算的配索方式是保证箱梁在长期使用状态下不出现结构性裂缝的最有效方法。

[1] 张文学.预应力混凝土连续箱梁不同布索方式对比分析[J].公路交通科技,2009,26(7):81-83.

[2] 浙江省交通厅公路管理局.预应力混凝土箱形连续梁桥裂缝调查分析及防治研究报告[R].杭州:浙江省交通厅公路管理局,2000．

[3] 方 志.预应力混凝土箱梁桥竖向预应力损失的实测与分析[J].土木工程学报,2009,39(5):79-81．

[4] 钟新谷.预应力混凝土连续箱梁桥裂缝防治与研究报告[R].长沙：中南大学,2001．

[5] 舒 彬.预应力混凝土连续箱梁裂缝分析与防治[J].四川理工学院学报(自然科学版),2008,21(4):105-107．