导管架式海洋平台的MRFD半主动模糊控制理论研究

霍发力, 曲鹏翔

(1.上海振华重工股份有限公司,上海200125;2.江苏科技大学,镇江212003)

导管架式海洋平台的MRFD半主动模糊控制理论研究

霍发力1, 曲鹏翔2

(1.上海振华重工股份有限公司,上海200125;2.江苏科技大学,镇江212003)

基于模糊理论控制采用磁流变阻尼器(MRFD)对海洋平台在规则波和随机波浪载荷、线性波和Stokes5节波作用下的振动控制效果进行研究。以平台的位移、速度响应为输入量,给出最优控制力的计算方法,并运用Morison方程实现了波浪力的数值仿真。以平台结构振动响应幅度为控制目标,设计MRFD系统,实现对海洋平台的最优控制。基于MATLAB调用ANSYS软件,开发平台振动控制界面,以典型导管架平台为例,进行多自由度数值仿真。仿真结果表明模糊控制下MRFD的半主动控制系统对海洋平台的动力响应有明显的控制效果。

海洋平台;模糊控制理论;磁流变阻尼器;半主动控制

0 前言

随着陆上建筑结构振动控制技术研究与应用不断成熟,海洋平台结构的振动控制技术已引起国内外学术界和工程界的重视,特别是磁流变、电流变阻尼器等新型控制器的研究与应用[1～3],为海洋平台的振动控制研究提供了更大的空间。欧进萍、杨飏等对海洋平台的冰、地震载荷振动控制进行了研究[4～6];李华军等对海洋平台波浪载荷的半主动振动控制进行了研究[7,8]。

在对海洋平台的数值模拟时,大多文献采用单自由度进行研究。把海洋平台简化为单自由度计算简单方便,但是仿真结果存在一定的误差。本文运用ANSYS有限元软件,以典型导管架平台为例,进行多自由度数值仿真。采用模糊控制理论研究海洋平台在规则波和随机波浪、线性波和Stokes5节波载荷下的磁流变阻尼器(MRFD)半主动振动控制理论,并通过一算例数值仿真了半主动MRFD对海洋平台的模糊控制效果。运用Matlab,开发了海洋平台半主动控制界面,更好地实现了海洋平台半主动控制。

1 导管架海洋平台结构的动力模型

1.1 海洋平台振动控制方程

带有MRFD的海洋平台运动方程表示如下:

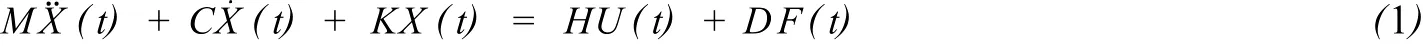
式中:X(t)=[x1,x2,…,xn]T是一n维位移向量;X¨(t)和X˙(t)分别表示对应的速度和加速度向量;M、C和K分别是质量、阻尼和刚度矩阵;F(t)表示外界载荷矩阵;D是外界载荷作用的位置矩阵;H表示磁流变阻尼器的位置矩阵;U(t)是磁流变阻尼器提供的控制力矩阵。其对应的状态空间方程为

式中Z(t)是2n维状态向量,式中各矩阵定义如下:

1.2 波浪载荷数值模拟[9]

运用Morison方程在时域内进行仿真波浪力。作用在海洋平台桩腿上的波浪力可表示为

式中:CD为拖曳力系数;CM为质量系柱体直径;ρ为海水密度;d为水深;z为积分变量;u(z,t)和˙u(z,t)分别为波浪水质点的水平速度和加速度。其中,u(z,t)和˙u(z,t)分别根据线性波浪理论和Stokes5节波理论分别求解,即可求出响应的随机波浪载荷和规则波浪载荷大小[9]。

2 模糊控制理论

2.1 模糊控制系统参量及参量的模糊化

本文采用二维模糊控制器(见图1),二维模糊控制器的两个输入基本上都选用受控变量及其给定值的偏差E和偏差变化EC。由于它能够较严格地反映受控系统中输出变量的动态特性,因此在控制效果上要比一维模糊控制器好得多。

图1 二维模糊控制器

对于应用于海洋平台的振动控制,模糊控制器的输入变量选取海洋平台的位移响应误差e(i)=rx(i)和误差变量ec(i)=e(i-1)-e(i),x为位移响应,r为参考输入,在振动控制中r=0,而输出变量选取模糊控制器的最优控制力。

2.2 建立模糊数模型[2]

为设计一个优良的模糊控制器,其关键是要有一个便于灵活调整的模糊控制规则。基于解析表达式的模糊数模型就具有这一规则。

双输入单输出模糊控制器所涉及的3个语言变量是:误差E、误差变化EC和控制量的变化U,即对应海洋平台的位移、速度和MRFD的控制力。本文采用的论域为[-3,3],通过响应的量化因子对论域进行模糊分割,3个语言变量被分割为7个模糊子集,它们分别为:{NBN M N S O PSPMPB}={-3,-2,-1,0,1,2,3}。

模糊数模型的结构可采用下列解析式来表达:

式中＜·＞表示四舍五入取整运算。

为使控制规则的修改更加灵活,满足系统在不同状态下对修正因子的不同要求,可在式(4)描述的模糊数模型中引入两个或两个以上的修正因子。

带4个修正因子的解析式可表示为

式中:αi,i=1,2,3,4∈[0,1]为修正因子,采用ITAE积分性能指标对多个修正因子寻优。

由于式(4)和式(5)的模糊量化取整运算,只有当E和EC恰好都是模糊数时才能准确地反映模糊控制规则。而在其他情况下只能近似地反映模糊控制规则,因此很不准确。由于量化误差的存在,不仅使模糊控制器的输出不能准确地反映控制规则,而且会造成调节死区,并在稳态阶段,使系统产生稳态误差,甚至产生稳态颤震现象。为了克服稳态性能差的缺点又不增加模糊控制器的复杂程度,宜采用泰勒二元函数在线插值模糊控制系统。

3 磁流变阻尼器

磁流变阻尼器具有能耗低、出力大、响应速度快、结构简单、阻尼力连续顺逆可调及可方便地与微机控制结合等优点,已经成为土木工程结构新一代高性能、智能化的减振装置,并已经在土木工程结构振动控制方面取得了初步的应用。

3.1 磁流变阻尼器力学模型

本文采用剪切阀式MRFD进行分析,根据Bing-ham流体在窄缝中流动的压力梯度方程,得到磁流变阻尼器力学分析模型[10]:

式中:L为导磁区长度;h为阻尼通道高度;D为缸体内径;d为活塞直径;v(t)为活塞与缸体间的相对速度;sgn为符号函数;τy为阻尼液的剪切屈服强度;η为阻尼液的表观黏度;cd为黏滞阻尼力系数;fdy为可调库仑阻尼力。

由阻尼力公式可知,阻尼力分为黏滞阻尼力和可调库仑阻尼力两种。其中库仑阻尼力可通过改变输入电流按需要调节。

3.2 半主动控制算法

本文采用简单的Bang-Bang磁流变阻尼控制算法,其可表示为

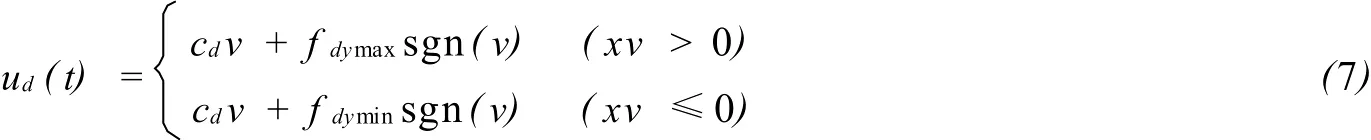
式中:x=xd是磁流变液阻尼器的相对位移。该控制算法表明,当磁流变液阻尼器所在位置,如结构层间背离平衡点振动时,需施加阻尼器能实现的最大阻尼力,否则,施加最小阻尼力。

4 算例

墨西哥湾某典型导管架海洋平台总质量为15 570 000 kg,上层建筑简化为八个集中载荷作用在顶层,水深125 m,等效高度160 m,桩腿直径2.2 m。本文以该平台为例,进行数值模拟。并运用ANSYS有限元软件建模,平台模型如图2所示。

磁流变阻尼器安装位置为第一、五层(自上而下)对角主桩腿上,如图2所示。

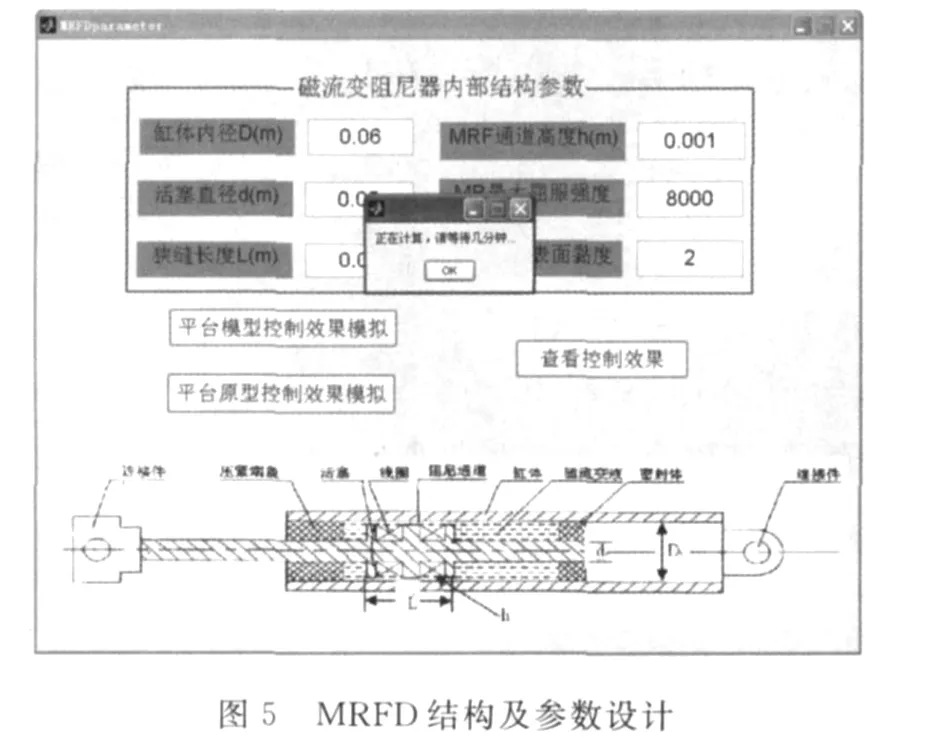
根据线形波浪理论进行分析,运用JONSWAP谱描述墨西哥湾某恶劣海况:有效波高10 m,周期为8 s。采用Morison方程,计算得到作用在海洋平台上随机波浪力(如图3～图4所示),并计算出在同等工况下规则波波浪力。运用ANSYS应用软件建立海洋平台模型,并计算出波浪力加载在海洋平台的X方向情况下,海洋平台的运动响应(位移、速度、加速度),以及在MRFD作用下的运动响应。MRFD结构及参数设计如图5所示。图6～图8所示为海洋平台顶层上NO.2节点的随机波浪载荷下运动响应及控制效果;MRFD半主动控制下,图9～图12为规则波中Stokes5节波作用下的响应及控制效果;图13～图16为规则波中线性波浪载荷的振动响应及控制效果。根据数值模拟效果可知:规则波浪载荷作用下控制效果明显好于随机波浪的控制效果,线性波载荷的控制效果好于Stokes5节波的控制效果。随机波浪的控制效果接近30%,规则波的控制效果接近40%;对速度、位移和加速度响应的控制效果中,加速度控制效果最好,位移控制效果次之,速度控制效果较差。

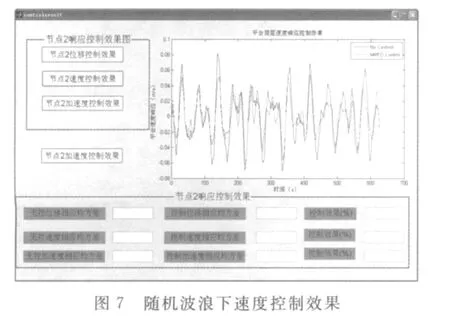
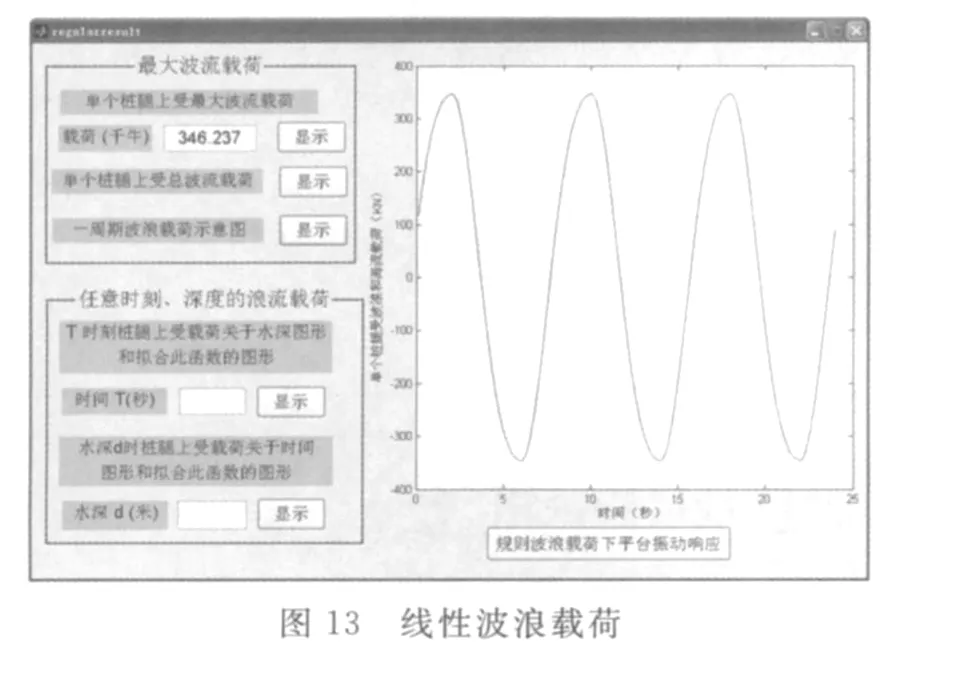
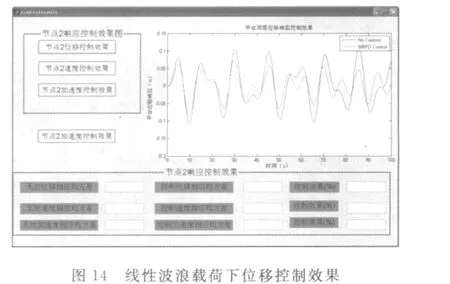
以上分析充分表明MRFD的半主动控制系统对海洋平台在随机波和规则波载荷作用下的位移、速度及加速度动力响应有明显的效果。

5 结束语

本文运用模糊控制理论并根据磁流变液的特性设计了MRFD的控制系统。运用MATLAB工具和ANSYS有限元软件,开发了固定式海洋平台半主动控制系统,模拟出了某典型导管架海洋平台多自由度模型在随机波浪荷载和规则波浪载荷作用下的动力响应,以及在MRFD控制下海洋平台的动力响应。计算结果表明,MRFD模糊半主动控制系统能够非常有效地控制海洋平台动力响应。其中,规则波要好于随机波,线性波要好于Stokes5节波,较大提高了海洋平台抗击随机载荷的能力,改善了海洋平台的工作环境。

[1] 祝世兴,田静,金平等.磁流变减震器结构及控制算法研究[J].机床与液压,2008,36(5):111-113.

[2] 王保兵,韩江水.MR阻尼器的特性试验研究[J].西安科技大学学报,2008,28(1):105-108.

[3] 张春巍,欧进萍.结构磁流变阻尼半主动控制的改进算法与仿真分析[J].世界地震工程,2003,19(1):37-43.

[4] 张纪刚,吴斌,欧进萍.海洋平台冰振控制试验研究[J].东南大学学报:自然科学版,2005,35(AO1):31-34

[5] 杨飏,欧进萍.导管架式海洋平台磁流变阻尼隔震结构的模型试验[J].振动与冲击,2006,25(5):1-5.

[6] 张纪刚,吴斌,欧进萍.渤海某平台磁流变智能阻尼隔振控制[J].沈阳建筑大学学报:自然科学版,2006,22(1):68-72.

[7] Li H J,Wang S Q,Ji C Y.Semi-Active Control of Wave-Induced Vibration for Offshore Platforms by Use of MR Damper[J].China Ocean Engineering,2002,16(1),33-40.

[8] Zhao D,Cai D M,Ma RJ,et al.The Vibration control of a combined anti-vibration platform under the rare seismic wave forces[C].Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering,OMAE 2007.

[9] 嵇春艳.海洋平台动力响应分析与振动控制技术研究[D].青岛:中国海洋大学.2003.

[10] 欧进萍.结构振动控制——主动、半主动和智能控制[M].北京:科学出版社,2003,71-75.

Research on MRFD Semi-Active Fuzzy Control Theory of Jacket Offshore Platforms

HUO Fa-li1, QU Peng-xiang2

(1.Shanghai Zhenhua Heavy Industries Co.,Ltd,Shanghai 200125,China;2.Jiangsu University of Science and Technology,Zhenjiang 212003,China)

A Magnetorheological Fluid Damper(MRFD)is adopted to control the vibration of the offshore platforms under regular wave and random wave,linear wave and Stokes5 wave loads based on the fuzzy control theory is studied.Taking the displacement and velocity of platforms as the inputs variables,the calculation means of the optimal control force is gave,and the numerical simulation of the wave force is calculated by Morison equation.Taking response amplitude of platforms structural vibration control as objectives,the MRFD system is designed optimally for controling the vibration platforms.Based on the MATLAB and ANSYS,design a control interface for the platforms,a typical platform as an example to make it multi-degree-of-freedom numerical simulation.The simulation results show that MRFD semiactive vibration control system is obviously effective on the offshore platforms.

offshore platform;fuzzy control theory;MRFD;semi-active control

P751

A

2009-09-13;修改稿收到日期:2009-12-28

国家自然科学基金资助项目(50609009)

霍发力(1982-),男,硕士,主要从事船舶与海洋工程方面的设计研究。

1001-4500(2010)02-0039-06