基于FLAC强度折减法的边坡稳定性分析

史 博，袁光明

(武汉理工大学 资源与环境工程学院，湖北 武汉 430070)

1 概述

边坡的稳定性，主要受岩土体本身和其结构面、夹层、夹层中充填物的物理力学参数控制。 边坡稳定性分析的计算方法，是边坡工程设计以及治理的主要内容，也是边坡应用的理论基础。目前，边坡的稳定性分析方法有很多种，归纳起来主要有极限平衡法、有限元法和极限分析法等。最常规的是极限平衡分析法，其特点是方便快捷，很多工程单位都采用该方法来计算、设计。然而，极限平衡分析法不能解决分析边坡应力和应变的问题。后来出现有限元分析边坡的稳定性，有限元在解决小变形方面有其优越性，但通常的边坡破坏为大变形问题，有限元在解决大变形方面不是十分方便。

随着计算机技术的发展和数值计算技术的提高，强度折减分析方法正成为边坡稳定分析研究的新趋势。对于复杂边坡的稳定分析，利用强度折减有限差分法，能考虑岩土体的非线性应力和应变关系，求得边坡内部每一计算点的应力应变及变形，同时可以对连续介质进行大变形分析，这样能比较真实地反映应力应变情况[1]。

本文把FLAC法和强度折减法结合起来形成强度折减有限差分法，进而分析边坡的稳定性问题，对岩土体材料的抗剪强度折减直至边坡达到临界破坏状态，从而得到安全系数。这样的做法，适用于任何复杂的边坡，与实际的边坡失稳过程较吻合。

2 边坡稳定性分析的FLAC强度折减法

2.1 FLAC法简述[2]

FLAC法，即连续介质快速拉格朗日差分分析方法(FLAC)，是用于研究连续介质在达到稳定塑流过程中的机制行为的显式有限差分程序。程序的结果，是由特殊的数学模型和专门的数值插值导出的。能较好地模拟地质材料在达到强度极限或屈服极限时发生塑性流动的力学行为，特别适用于分析渐进破坏和失稳及模拟大变形问题。

FLAC法基本原理类同于离散单元法，但它却能象有限元那样适用于多种材料模式与边界条件的非规则区域的连续问题求解。在求解过程中，FLAC又采用了离散元的动态松弛法，不需求解大型联立方程组，便于计算。另外，FLAC法不但能处理一般的大变形问题，而且能模拟岩体沿某一软弱面产生滑动的变形。FLAC法能针对不同的材料特性，使用相应的本构方程来比较真实地反映实际材料的动态行为。FLAC法还可考虑锚杆、挡墙、抗滑桩等支护结构与围岩的相互作用。

2.2 强度折减法(strength reduction methods)基本原理[3，4]

目前，数值分析方法一般只能得出边坡的应力、位移、塑性区等，无法得到边坡危险滑面以及相应的安全系数。强度折减法将强度折减技术与数值模拟方法相结合，在给定的评判指标下，通过调整折减系数对边坡的稳定性进行分析，求得边坡的最小稳定安全系数。其基本原理是将岩土体强度指标c、φ值同时除以一个折减系数F，得到一组新的c′、φ′，作为材料新的参数进行数值计算。当边坡岩土体符合给定的临界破坏状态判定条件时，对应的F称为边坡的最小安全系数。

2.3 FLAC强度折减法步骤[5]

根据边坡抗滑稳定安全系数的定义，运用弹塑性理论，FLAC强度折减法求解边坡抗滑稳定安全系数的迭代步骤，如图1所示。

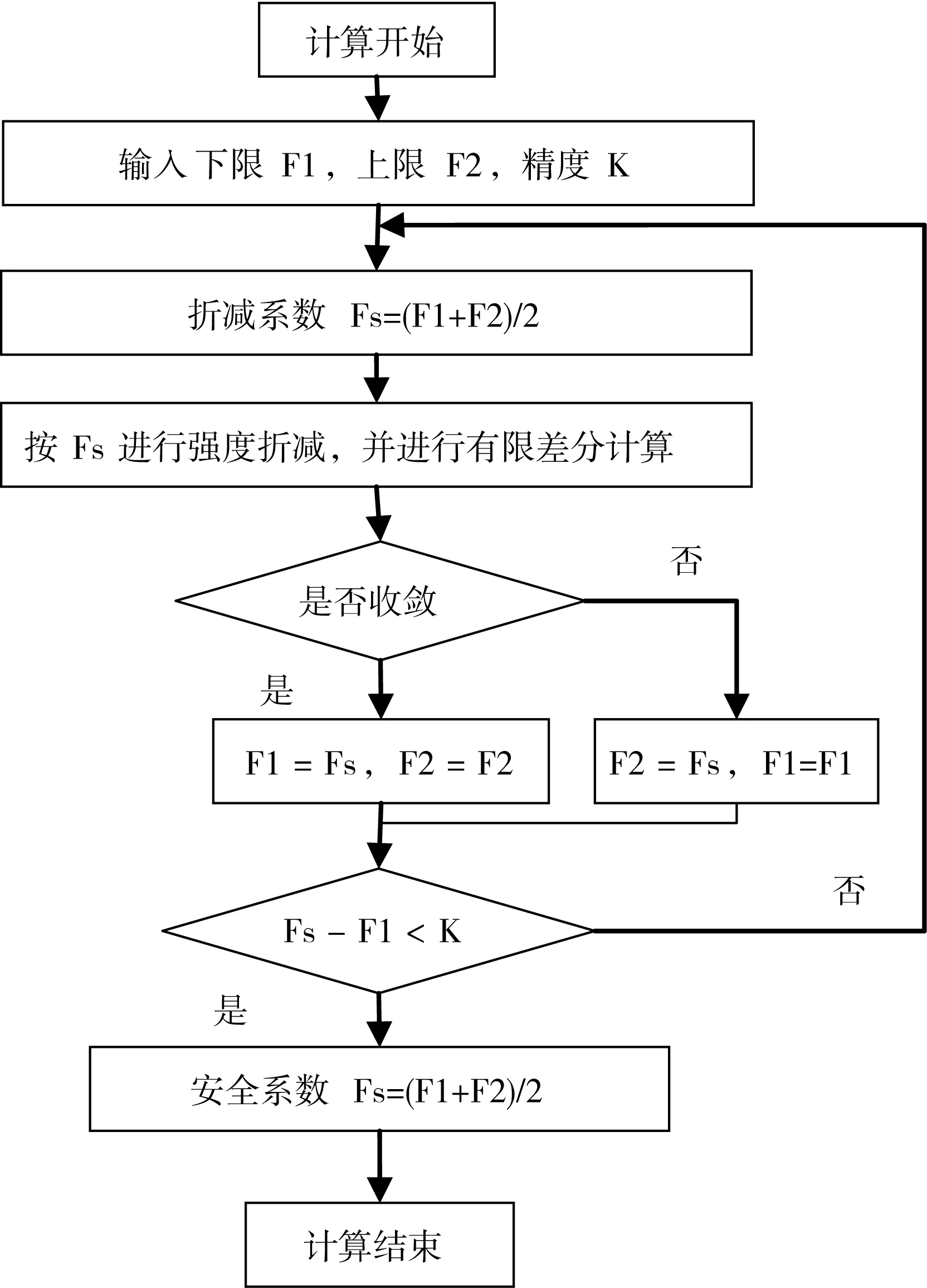
图1 FLAC强度折减法计算流程图

3 汉阳港区专用线改建工程边坡稳定性分析

3.1 工程概况

汉阳港区专用线隧道位于武汉市拦江大道旁，起始里程DK4+900，终点里程DK7+400，隧道建筑长度2500m。主通道北端起始里程DK4+900，终点里程DK5+665，长度为765m，采用钢筋混凝土U形槽结构。洞身明挖暗埋段起始里程为DK5+655，终点里程DK6+145，长度为480m，采用明挖暗埋矩形钢筋混凝土结构。南端引导段起始里程为DK6+145，终点里程DK7+400，长度为1255m，采用钢筋混凝土U形槽结构。

考虑到该隧道边坡比较长，为简化计算模型，本文选取具有代表性的DK5+905～DK5+935暗埋段隧道边坡断面进行分析，边坡高度10m，上部0～4m采用1∶2.5放坡，4～7m采用1∶3放坡，下部7～10m采用1∶3放坡。根据地质调查，现场钻探坑探、物探、原位测试及室内岩土试验成果，其边坡形态及土层分布如下图2所示。

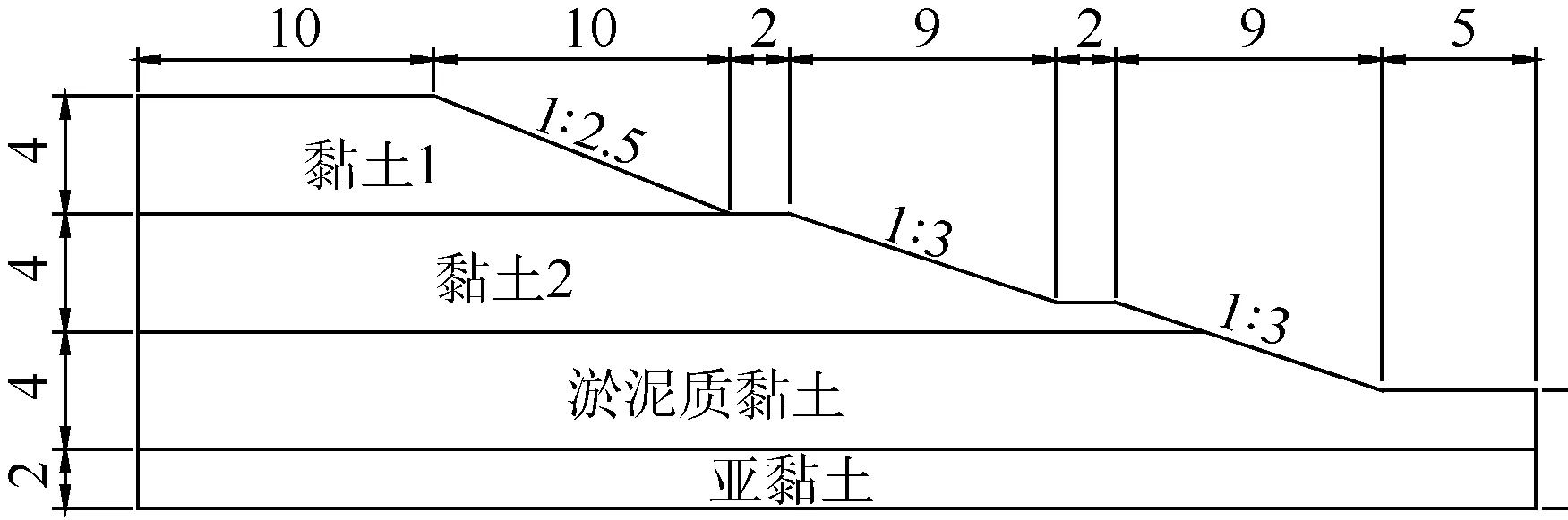
图2 脉冲放电单位体积能量消耗与其他碎岩方法的比较

3.2 计算参数

在土体稳定性的计算分析中，抗剪强度(土的内摩擦角和黏聚力)是其中最重要的计算参数。而对于黏性土来说，影响其抗剪强度指标的因素又很复杂。在充分踏勘调查的基础上，本文选取了边坡典型地段有代表性的岩土试样，在野外做了现场原位大剪试验和配套的室内物性试验。钻探揭露的岩土体物理力学性质见表1。

表1 各岩土层力学参数

3.3 FLAC计算模型的建立

模型的建立按照如下原则进行：

①计算所使用的坐标系垂直方向为y轴，水平方向为x轴。②采用Mohr-Coulomb本构模型。由于斜坡的变形和破坏主要发生在坡体的浅部，构造应力在长期的地质过程中已松弛殆尽。因此，模型边界不考虑水平构造应力的作用，只考虑自重应力的作用。③初始地应力为自重地应力场，垂直应力σy=γH，水平应力由岩土体泊松关系确定。④由于轴向变形可以忽略，故本计算属于平面应变问题。⑤计算中不考虑地下水及地震的影响。⑥边界条件为:左右侧边界作X方向约束，底部作Y方向约束，开挖面为自由面。⑦计算参数的选取:岩体的计算参数按照表1选取。

根据上述原则，结合工程边坡形态和岩层分布状况，所建立模型如图3所示。

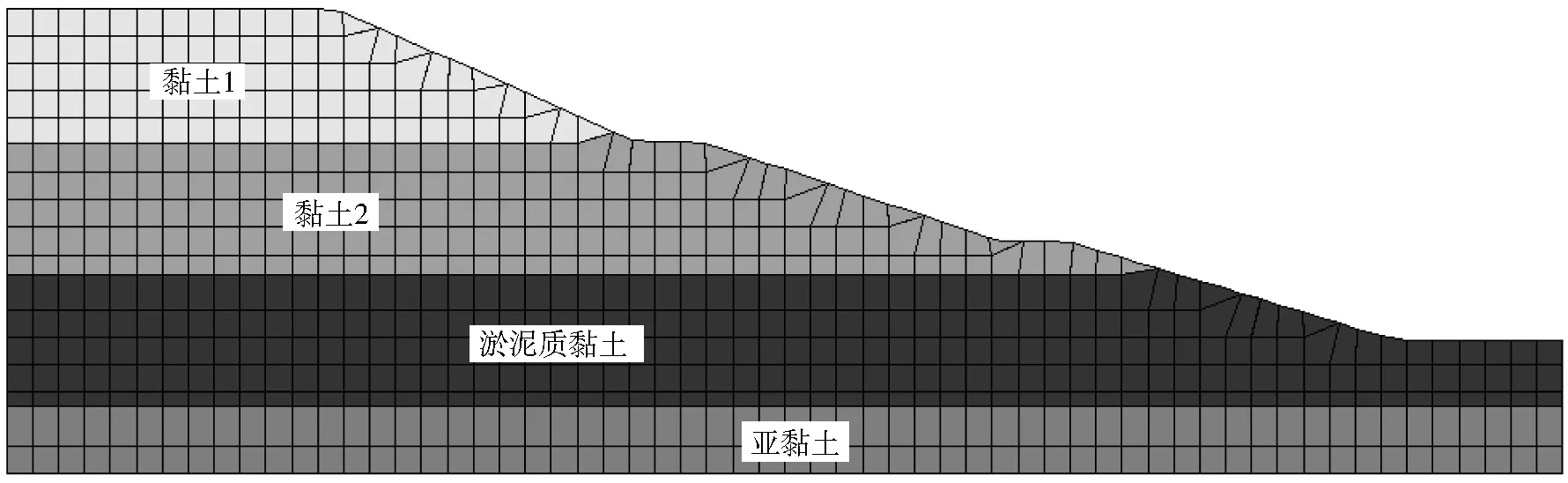
图3 隧道边坡模型

依据上述模型，当计算不再收敛时， 汉阳港区专用线隧道边坡的滑移面图见图4。为了对比分析FLAC强度折减法的可靠性，应用Slope/w[6]中的Janbu法所得的模拟结果如图5所示。

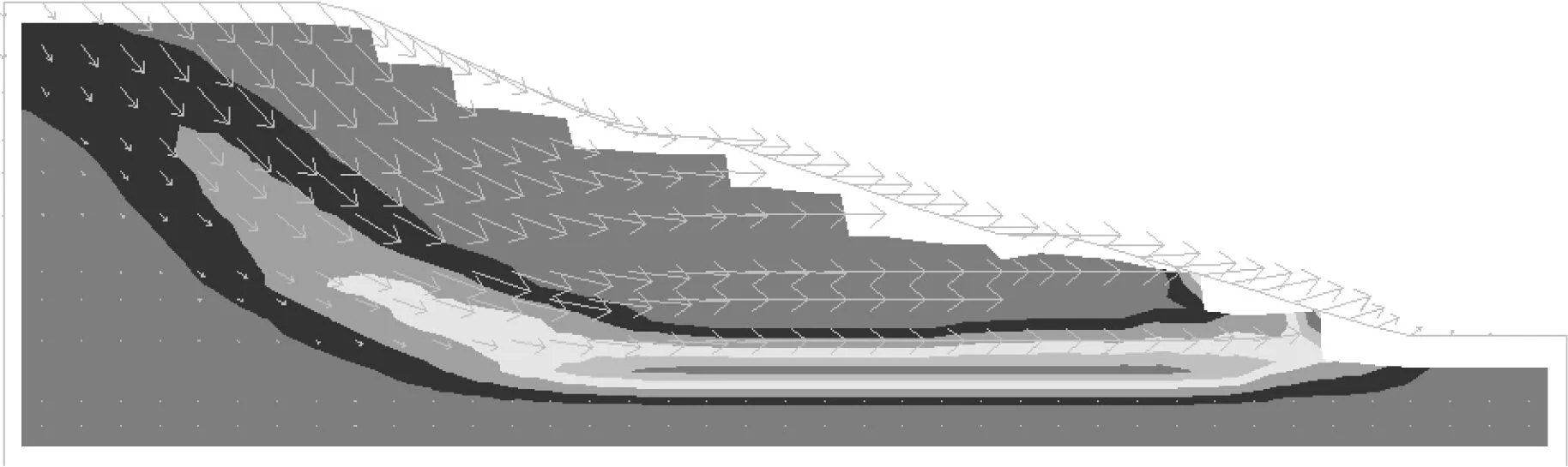
图4 汉阳港区专用线隧道边坡的滑移面图(FLAC强度折减法)

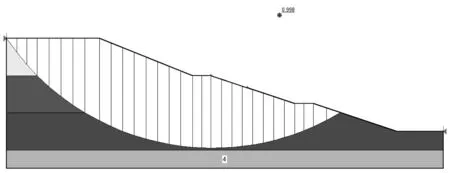
图5 汉阳港区专用线隧道边坡的滑移面图(Janbu法)

3.4 数值模拟结果及分析

数值模拟计算结果见表2。FLAC强度折减法求得边坡的安全系数与传统极限平衡法求得的比较接近，数值上略小。

由表2可以看出，FLAC强度折减法所得的安全系数最小，但与极限平衡条分法相比相差不大，其中FLAC强度折减法和Janbu法所得的安全系数小于1，说明该边坡处于不稳定状态，极有可能发生滑坡；Morgenstern-Price法和Bishop法均略大于1，说明边坡处于极限平衡状态。通过对该边坡的长期监测，该边坡最终发生了破坏，说明FLAC强度折减法对于计算边坡稳定性是完全可行的，结果是可靠的，此方法可推广使用。

表2 汉阳港区专用线隧道边坡稳定系数表

4 结 语

基于强度折减理论的显式拉格朗日有限差分法分析土坡稳定性，具有计算简单方便、结果可靠的优点，同时避免了极限平衡法需要事先假设滑动面以及人为假定等不足[7]。

将FLAC强大的数值计算能力与强度折减技术相结合，以广义剪应变发展与数值计算的不收敛性作为边坡失稳的评价依据，形象地描绘出了边坡失稳形态，为准确判定边坡的真实受力状态提供可靠的依据。此方法可以较为准确地通过最大剪应变增量和剪应变速率自动地搜索出滑坡潜在滑动面或剪切错动面，判断岩土体的稳定性状况。通过汉阳港区专用线隧道边坡稳定性分析表明，强度折减所确定的边坡安全系数与Janbu法、简化的Bishop法及Morgenstern-Price法所得的结果十分接近，滑面的形状及位置也极为相似，与实际监测结果完全吻合。因此，该方法是合理可行的，对分析类似岩土边坡工程具有借鉴意义[8]。

[1] 程海英，等.边坡稳定及加固分析的FLAC强度折减法[J].中国科技论坛，2006(3)：22-24.

[2] 江德飞，何光春.传递系数法与FLAC强度折减法比较分析——以猴子石滑坡分析为例[J].重庆交通学院学报，2005，24(1)：94-99.

[3] DAWAON EM，ROTHWH and DRESCHER A. Slope stability analysis by strength reduction[J]. Geotechnique，1999，49:835-840.

[4] 吴明，傅旭东，刘欢.边坡稳定分析中的强度折减法[J].土工基础，2006，20(1): 49-52.

[5] 欧湘萍，白楷，朱云升，袁灿，等.基于FLAC-3D的强度折减法边坡稳定性分析[J].武汉理工大学学报，2009，31(9)：59-61.

[6] 高涛，毛巨省，罗建峰，等.SLOPE/W程序在土质边坡稳定性分析中的应用[J].西安科技大学学报，2006，26(2)：184-188.

[7] 迟世春，关立军.基于强度折减的拉格朗日差分方法分析土坡稳定性[J].岩土工程学报， 2004， 26 (1): 42-46.

[8] 刘娉慧，房后国，黄志全，刘煊.FLAC强度折减法在边坡稳定性分析中的应用[J].华北水利水电学院学报，2007，28(5)：52-58.