随从力作用下热弹耦合轴向运动梁的稳定性*

郭旭侠，王忠民

（1.西安理工大学理学院，陕西 西安 710054；

2.宝鸡文理学院机电工程系，陕西 宝鸡 721007）

随从力作用下热弹耦合轴向运动梁的稳定性*

郭旭侠1，2，王忠民1

（1.西安理工大学理学院，陕西 西安 710054；

2.宝鸡文理学院机电工程系，陕西 宝鸡 721007）

研究了切向均布随从力作用下热弹耦合轴向运动梁的稳定性问题。建立了热弹耦合轴向运动梁在随从力作用下的运动微分方程，采用归一化幂级数法，推导出了2种边界条件下热弹耦合轴向运动梁在随从力作用下的特征方程。计算了系统的前3阶量纲一复频率，分析了量纲一运动速度、量纲一热弹耦合系数和量纲一随从力等参数对梁的稳定性的影响。

固体力学；稳定性；随从力；轴向运动梁；热弹耦合；幂级数法

1 引 言

非保守力对工程系统中构件的稳定性影响很大，空中飞行的飞机、导弹受到的气体摩擦力、输流管道中流体的粘滞阻力等都属于非保守力。对随从力（非保守力）作用下构件的动力稳定性问题已有很多研究：赵凤群等［1］用积分方程法研究了具有多个点弹性支承的Kelvin型粘弹性简支杆在切向均布随从力作用下的动力特性和稳定性问题；M.A.Langthjem等［2］研究了随从力作用下粘弹性杆件的动力稳定性；禚瑞花等［3］采用幂级数法得到了三参量模型粘弹性非保守梁的特征方程，分析了不同边界条件下粘弹性梁的稳定性；R.F.Fung等［4］采用Galerkin法研究了同时受到随时间变化的轴向和横向载荷作用的三参量模型粘弹性梁的动力稳定性。但是，这些研究均没有考虑温度改变对系统稳定性的影响。F.L.Guo等［5］用蒙特卡罗方法计算了两端固支耦合热弹梁的振动频率；Y.X.Sun等［6］研究了考虑耦合热弹阻尼时微型梁的振动特性，结果表明考虑耦合效应时的振动频率大于非耦合时的振动频率。轴向运动梁作为工程实际中的构件之一，热弹耦合条件下在切向均布随从力作用下的稳定性问题却少有报道。

本文中试图采用归一化幂级数法，得到不同边界条件下热弹耦合轴向运动梁的特征方程，分析量纲一运动速度、量纲一热弹耦合系数和量纲一随从力等参数对梁的稳定性的影响。

2 运动微分方程

图1所示为弹性矩形截面梁，沿x方向的运动速度为v，受到切向均布随从力q0的作用。梁的跨度为L，宽度为b，高度为h，材料密度为ρ，弹性模量为E。设梁的初始温度为τ0，任一瞬时t梁的温度改变为T＝T（z，t）。

切向均布随从力作用下热弹耦合轴向运动梁的运动微分方程为［1，7］

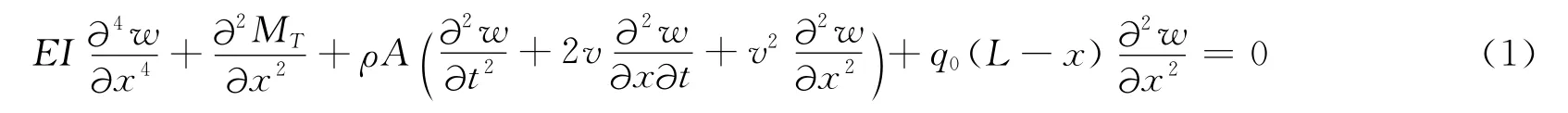
式中：梁在z方向的位移w＝w（x，t）；热弯矩MT＝bEαT∫h／2－h／2Tzdz，其中αT为线热胀系数；梁的横截面面积A＝bh；横截面惯性矩I＝bh3／12。

梁的热传导方程为［8］

式中：导温系数a＝k／（ρcV），k为导热系数，cV为比定容热容。

求解方程（5b），得

梁的两端恒温时，边界条件为

3 幂级数法及特征方程

设式（7）的解为

式中：Bn是待定常数，Vn（ξ）为基本解，即

式中：ωo、ωd分别表示ω的实部和虚部。

由于f、g 中含有待定系数dn，i＋2、en，i＋2、dn，i＋1、en，i＋1、dn，i、en，i，式（12）被称为待定系数的递推公式。

由幂级数解的归一化条件可知［9］

式（15a）中B2、B4不全为0，式（15b）中B3、B4不全为0，因此式（15a）和（15b）的系数行列式为0，得

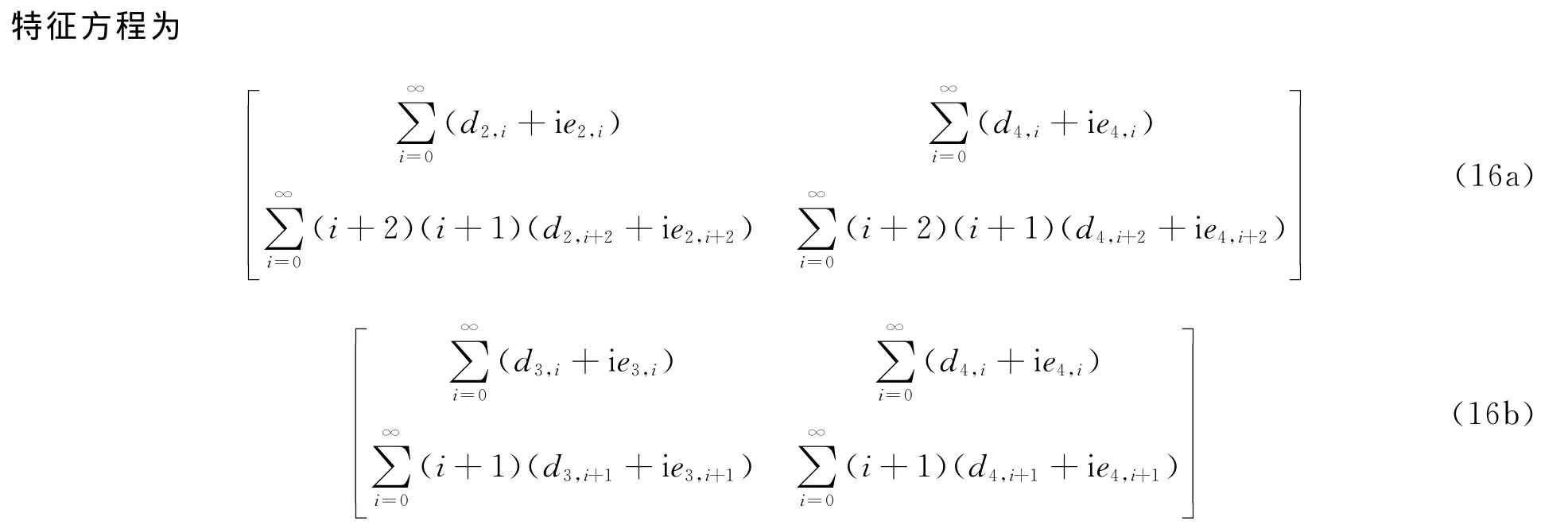
分别求解方程（16a）和（16b），即可得到2种边界条件下，受切向均布随从力作用时热弹耦合轴向运动梁的复频率。从而分析量纲一运动速度、量纲一热弹耦合系数和随从力等参数对梁的稳定性的影响。

4 计算结果与分析

当λ＝0，c＝0，q＝0时，方程（7）退化为弹性梁自由振动的振型方程。首先计算弹性梁自由振动时的前3阶固有频率和1阶临界载荷，计算结果与文献的比较见表1。计算时i＝50。

表1 弹性梁前3阶固有频率和1阶发散载荷的本文解与文献中解的比较Table 1 Comparison of the first three orders natural frequencies and the divergence load of the first order for elastic beams with those in reference

4.1 两端简支梁

图2～4分别表示不同条件下梁的量纲一复频率与量纲一运动速度之间的关系。图2中量纲一热弹耦合因子λ＝0，量纲一随从力q＝10；图3中λ＝0.2；图4中q＝15。比较图2～4可知，其他参数相同，q＝10，当λ从0增大到0.2时，第1阶模态的发散临界速度c由2.20变为2.63；当λ＝0.2时，q由10增大到15，此时，第1阶模态的发散临界速度c由2.63减小到2.06。图2～4中的第2阶模态都出现了单一模态颤振失稳，只是条件不同产生颤振失稳时的临界速度不同。其他参数相同时，第2阶模态颤振失稳时的临界速度随量纲一热弹耦合因子的增大而增大，随量纲一随从力的增大而减小。

图2 量纲一复频率随量纲一运动速度的变化曲线Fig.2 Dimensionless complex frequencies versus dimensionless moving speeds

图3 量纲一复频率随量纲一运动速度的变化曲线Fig.3 Dimensionless complex frequencies versus dimensionless moving speeds

图4 量纲一复频率随量纲一运动速度的变化曲线Fig.4 Dimensionless complex frequencies versus dimensionless moving speeds

图5、6分别表示不同条件下，量纲一复频率与量纲一随从力之间的关系曲线。图5中量纲一运动速度c＝1，可以看出随着热弹耦合因子的增大，第1、2阶模态的发散载荷也增大；图6中量纲一运动速度c＝3。比较图5、6可知，其他参数相同的条件下，随着量纲一运动速度的增大，第1阶模态的发散载荷减小。由于参数的改变，图6中第2阶模态出现了单一模态颤振失稳。

图5 量纲一复频率随量纲一随从力的变化曲线Fig.5 Dimensionless complex frequencies versus dimensionless follower forces

图6 量纲一复频率随量纲一随从力的变化曲线Fig.6 Dimensionless complex frequencies versus dimensionless follower forces

4.2 两端固支梁

图7、8分别表示不同条件下，量纲一复频率与量纲一运动速度之间的关系曲线。图7中量纲一随从力q＝40，从图中可以看出随着量纲一热弹耦合因子的增大，第1阶模态的临界速度增大。图8与图7相比，q增大到60，其他参数相同条件下，随着量纲一随从力的增大，第1阶模态的临界速度减小。图7、8中的第2阶模态也出现了单一模态颤振失稳，而且产生颤振失稳时的临界速度随着参数的改变而变化。

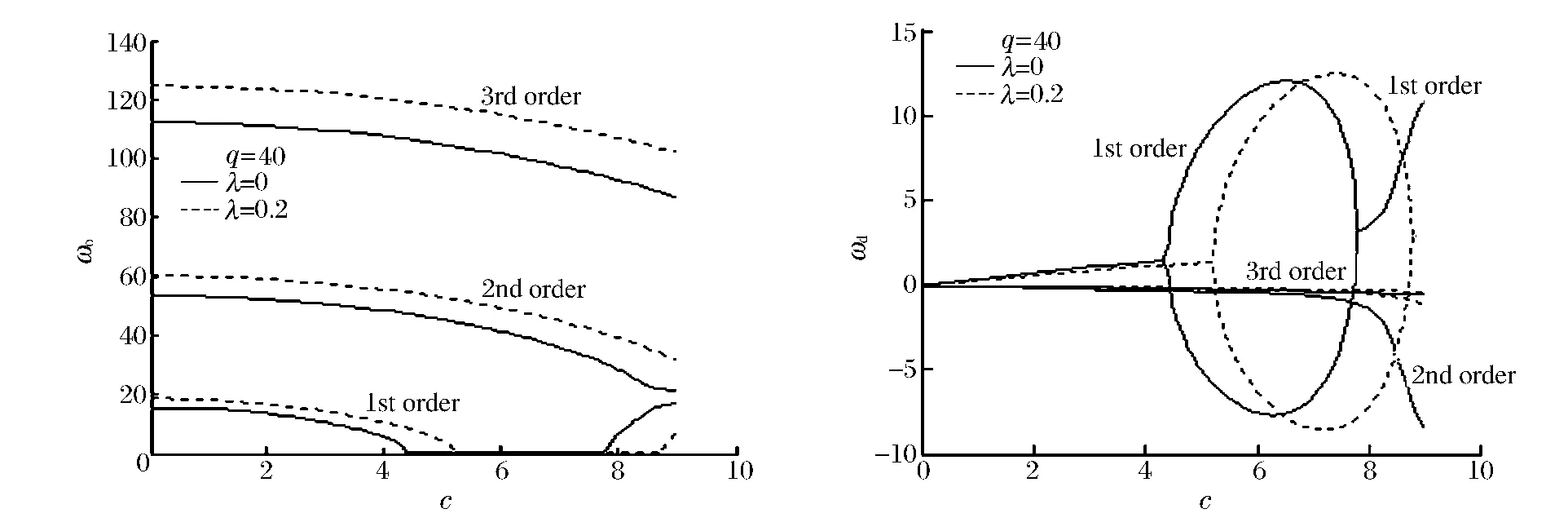
图7 量纲一复频率随量纲一运动速度的变化曲线Fig.7 Dimensionless complex frequencies versus dimensionless moving speeds

图8 量纲一复频率随量纲一运动速度的变化曲线Fig.8 Dimensionless complex frequencies versus dimensionless moving speeds

图9、10分别表示不同条件下，量纲一复频率与量纲一随从力之间的关系曲线。图9中量纲一运动速度c＝1，随着量纲一热弹耦合因子的增大，第1阶模态的临界载荷q由78.5增大到93.1，第2阶模态没有出现发散失稳。图10中量纲一运动速度c＝3，随着量纲一热弹耦合因子的增大，第1阶模态的临界载荷也增大。图9与图10相比，其他参数相同的条件下，随着量纲一运动速度的增大，第1阶模态的临界载荷减小。

图9 量纲一复频率随量纲一随从力的变化曲线Fig.9 Dimensionless complex frequencies versus dimensionless follower forces

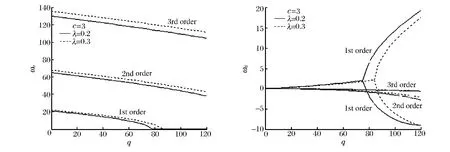
图10 量纲一复频率随量纲一随从力的变化曲线Fig.10 Dimensionless complex frequencies versus dimensionless follower forces

5 结 论

计算结果表明：其他参数相同的条件下，随着热弹耦合因子的增大，第1阶模态的临界速度和临界载荷都增大；增大量纲一运动速度，第1阶模态的临界载荷减小；第1阶模态的临界速度随着量纲一随从力的增大而减小。

［1］赵凤群，王忠民.点弹性支承下非保守粘弹性杆的稳定性分析［J］.西安理工大学学报，2003，19（3）：230-234.

ZHAO Feng－qun，WANG Zhong-min.Stability analysis of viscoelastic rod with elastic point supports subjected to nonconservative forces［J］.Journal of Xi’an University of Technology，2003，19（3）：230-234.

［2］Langthjem M A，Sugiyama Y.Dynamic stability of viscoelastic beam under follower forces［J］.Journal of Sound and Vibration，2000，238（5）：809-851.

［3］禚瑞花，冯叔忠.粘弹性梁在随从力作用下的动力稳定性［J］.工程力学，2005，22（3）：26-30.

ZHUO Rui-hua，FENG Shu-zhong.Dynamic stability of viscoelastic beam under follower forces［J］.Engineering Mechanics，2005，22（3）：26-30.

［4］Fung R F，Huang J S，Chen W H.Dynamic stability of viscoelastic beam subjected to harmonic and parametric excitations simultaneously［J］.Journal of Sound and Vibration，1996，198（1）：1-16.

［5］Guo F L，Rogerson G A.Thermoelastic coupling effect on a micro-machined beam resonator［J］.Mechanics Research Communications，2003，30（6）：513-518.

［6］Sun Y X，Fang D N，Ai K S.Thermoelastic damping in micro-beam resonators［J］.International Journal of Solids and Structures，2006，43（10）：3213-3229.

［7］Guo X X，Wang Z M，Wang Y，et al.Analysis of the coupled thermoelastic vibration for axially moving beam［J］.Journal of Sound and Vibration，2009，325（3）：597-608.

［8］严宗达，王洪礼.热应力［M］.北京：高等教育出版社，1993.

［9］周银锋，王忠民，王砚.考虑随从力作用的运动粘弹性板的动力稳定性［J］.工程力学，2009，26（1）：25-30.

ZHOU Yin-feng，WANG Zhong-min，WANG Yan.Dynamic stability of moving viscoelastic plate subjected to follower forces［J］.Engineering Mechanics，2009，26（1）：25-30.

［10］倪振华.振动力学［M］.西安：西安交通大学出版社，1990.

Thermoelastic coupling stability of the axially moving beam subjected to follower force＊

GUO Xu-xia1，2，WANG Zhong-min1
（1.School of Sciences，Xi’an University of Technology，Xi’an710054，Shaanxi，China；
2.Mechanical and Electrical Engineering Department，Baoji University of Arts and Sciences，Baoji 721007，Shaanxi，China）

The thermoelastic coupling stability of the axially moving beam under the action of uniformly distributed tangential follower forces was investigated.The differential equation of motion for the axially moving beam under the action of uniformly distributed tangential follower forces was established，and the eigenequation for the axially moving beam with two kinds of boundary conditions subjected to follower forces was derived by a normalized power series method.The first three orders dimensionless complex frequencies of the system were calculated，and the effects of the dimensionless moving speed，the dimensionless thermoelastic coupling factor，the dimensionless follower forces on the stability of the axially moving beam in the thermoelastic coupling case were analyzed.

solid mechanics；stability；follower force；axially moving beam；thermoelastic coupling；power series method

23July 2009；Revised 14December 2009

GUO Xu-xia，gxx5432106＠sina.com

（责任编辑 曾月蓉）

O347.2 国标学科代码：130·15

A

1001-1455（2010）06-0614-08

2009-07-23；

2009-12-14

国家自然科学基金项目（10872163）；陕西省教育厅科学研究计划项目（08JK394）；宝鸡文理学院重点项目（ZK09147）

郭旭侠（1976— ），女，博士研究生，讲师。

图1随从力作用下的热弹耦合轴向运动梁

Fig.1An axially moving beam in the thermoelastic coupling case subjected to follower force

Supported by the National Natural Science Foundation of China（10872163）