2010年全国卷Ⅰ压轴题中的“多种圆”

陈凭心

(安徽灵璧中学,安徽灵璧 234200)

2010年全国卷Ⅰ压轴题中的“多种圆”

陈凭心

(安徽灵璧中学,安徽灵璧 234200)

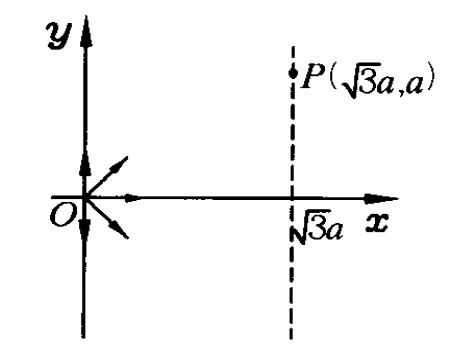
图1

2010年普通高校招生全国卷Ⅰ第26题:如图1,在0≤a区域内存在与xy平面垂直的匀强磁场,磁感应强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0～180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上

P(3a,a)点离开磁场.求:

(2)此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围;

(3)从粒子发射到全部粒子离开磁场所用的时间.

题给条件:在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0～180°范围内.由条件知,所有粒子的初速度矢量未端在以O为圆心的圆上,故此圆称为“矢端圆”,见图2中圆O.

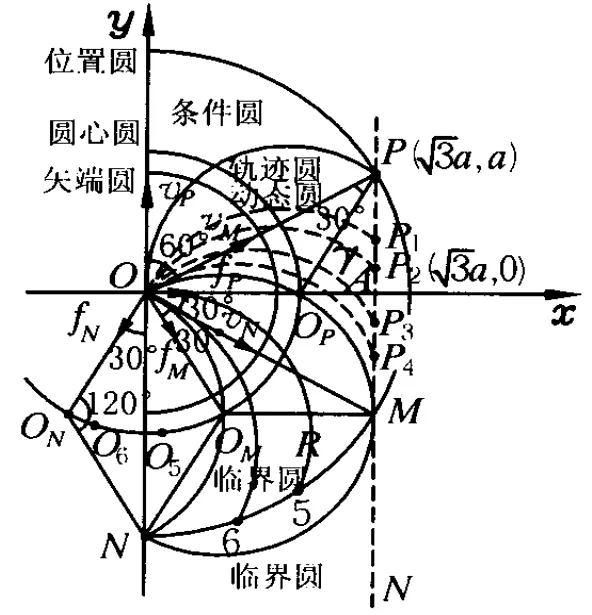
图2

由“已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P(3a,a)点离开磁场”,题中虽然未给出磁场方向及粒子电性,但由沿y轴正方向发射的粒子打到P点,刚发射时该粒子所受洛伦兹力必沿x轴正方向,圆心必在x轴上,在x轴上以某点为圆心,以适当长度为半径作圆OP过O、P点,可称作“轨迹圆”,由于此圆是由题给条件作出,亦可称“条件圆”,其他所有粒子轨道半径与其相等,环绕方向与其相同.

由于所有粒子都从O点开始作匀速圆周运动,且轨道半径相等,故所有粒子作圆周运动的圆心,都在以O为圆心,R为半径的圆上,此圆称之为“圆心圆”.随发射出的粒子与y轴正方向夹角不断增大,粒子作圆周运动的圆心也由OP点在圆心圆上顺时针移动,可在图2中作出一系列“动态圆”,这些粒子分别从P1…P4点穿出磁场右边界.

t0时刻仍在磁场中的粒子,与打到P点的粒子相比,应该在相同的时间内走过的弧长相等,对应的弦长度相等,即该时刻在磁场中的粒子到O点的距离相等,即在以O为圆心,以OP为半径同一时刻“位置圆”上.

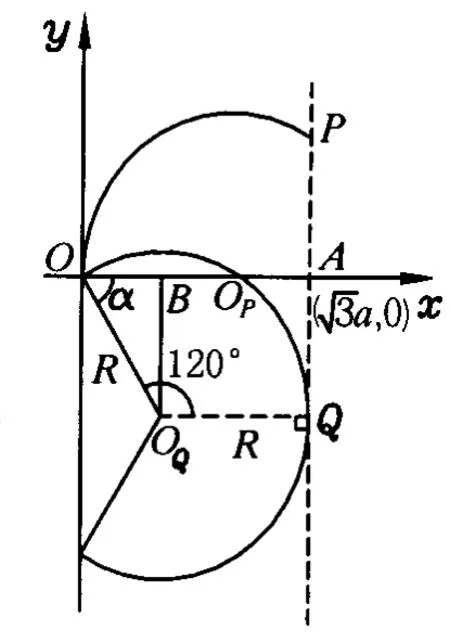
图3

t0时刻在位置圆上MN上的粒子仍在磁场中,其圆心在圆心圆上自OM至ON之间的O5、O6等位置,其轨迹如图 2中的圆OM、O5、O6、ON等一系列动态圆;在这些动态圆中,M、N是在磁场中的临界位置,圆OM、ON为“临界圆”,因P、M关于x轴对称,∠OOMM=∠OOPP= 120°,OOM⊥OOP,且速度方向与半径垂直,打到M点的粒子初速度沿OP方向,与y轴正方向夹角60°,又∠OONN=120°,∠ONON=30°,vN⊥OON,与y轴负方向夹角为60°,与y轴正方向夹角为120°,故t0时刻仍在磁场中的粒子的初速度与y轴正方向夹角为60°≤θ≤120°.

2010-07-06)