一类具有时滞和带毒素的功能性反应的植物-食草动物系统性态分析
沈莉莉,赵维锐
(武汉理工大学 理学院,湖北 武汉 430070)
20世纪80年代以来,植物在动物-植物系统中的作用倍受生态学家的关注[1],植物因食草动物“捕食”而受损害,但植物不是完全被动的,植物有各种补偿机制以及防护作用.在长期的进化过程中,有些植物形成一定的毒性用于防御食草动物的觅食活动.这些带毒素的植物在被食草动物觅食后,会对动物产生潜在的生理影响.大量的研究表明:植物次生化合物(包括植物的气味,味道以及毒素等)对食草动物的食物摄入[2]、蛋白质利用率、酶活性、肝脏和肾脏细胞膜的完整性、生长速度、存活以及繁殖均具有显著的抑制作用[3].因此在研究动物-植物系统的相互作用时考虑毒素的作用能使理论更真实的反应现实.20世纪80年代初,以J.P.Bryant和R.K.Swihart等为代表的数学家在研究动物-植物系统的相互作用时开始考虑了毒素的作用.而在本世纪初,以冯芷兰、闫慧臻等为代表的中国学者开始了对毒素在植物-食草动物系统作用以及毒素对个体生长模型的影响的研究,并得到了一系列较好的成果.但美中不足的是这些模型中都没有纳入对时滞的考虑.
为了能够更好的研究动植物系统的动力学行为,本文就一类具有时滞和带毒素的功能性反应的植物-食草动物系统进行分析,研究植物-食草动物的相互动态.
1 模型分析
最常用的研究植物-食草动物生态系统的模型为传统的Holling-II型功能性反应[4]:
(1)
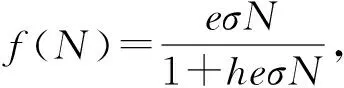
(2)
e为食草动物的觅食率,其大小取决于捕食者的移动速度以及捕食者能侦测到的食饵的分布区域的半径大小.σ是N的函数,为食草动物的消化率,h为捕食者对每一份食饵的掌控时间,即为食草动物消化每一份食物所需的时间.r是植物的内禀增长率,K为环境容纳率,B为被消耗的植物量转换成新的动物量的转换率(通过增长和繁殖),d为食草动物的与植物毒素无关的死亡率.显然这里食草动物的增长率是植物密度的单调递增的函数.但当我们在系统中考虑到植物毒素的影响时,这种假设就不合适了,因为当植物密度达到一定程度时,植物毒素对食草动物的防御作用会导致食草动物生长率的降低.为了刻画植物毒素对食草动物的影响,冯芷兰,刘荣松等学者在传统的Holling-II型功能性反应中加入了毒素对食草动物成长的影响的功能性反应:
(3)
则原来的系统变为:
(4)
在自然界中,很多现象都具有时间滞后性.有的现象受时间滞后的影响并不大,而有些现象则不然,它们在受到时间滞后影响时原系统和影响后的系统差别特别大.这时,必须考虑时间滞后这一因素.特别是在生态系统中,这种时间滞后更不容忽略.同样,在现实中食草动物通过觅食而得到增长和繁殖(即消耗的植物量转换成新的动物量)这个过程是需要一定的时间来实现的.为了分析这一段时间对系统稳定性的影响,引进滞量τ,对原系统做如下改变:
(5)
在这部分假设食草动物能控制自己的消化率,当植物密度足够大的时候,食草动物就会减少自己对植物的消化量.故设定一个阈值Nm:当植物量N不高于阈值Nm时,食草动物的消化率为常数;当植物量N超过阈值Nm时,食草动物的消化率就是植物量N的递减函数.
(6)
这里的σ0>0是一个常量.在对σ(N)做了如上假设之后,C(N)也发生了变化,故不妨假设:
(7)
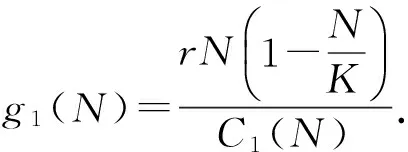
(8)
则可将系统(5)改写成:
(9)
2 平衡点及其稳定性
系统(9)有两个边界平衡点:E0=(N0,P0)=(0,0)以及Ek=(Nk,Pk)=(k,0).同时系统只有一个正的内部平衡点,将其记作E*=(N*,P*),其中0
其中Δv=BG(BG-d).
(10)
E*是否为内部平衡点是由N*和K的值的大小来决定的:只有当N* (11) (12) 在做了如上假设之后,可以得到以下结论:在(G,ω)平面上,只要满足条件ω>ωk(G),则内部平衡点E*总是存在. 这是因为G 下面来考虑边界平衡点E0和EK的稳定性: 定理1 (1)E0总是鞍点; (2)当ω<ωk(G)时EK是稳定的,而当ω>ωk(G)时EK不稳定. 证明由于边界平衡点E0和EK对于所有的G和ω都是存在的,从而很容易就能得到它们的稳定性. 当ω>ωk(G)时,也即是BC1(K)>d,则λ2=BC1(K)-d>0, 故EK为鞍点,从而EK是不稳定的. 当ω<ωk(G)时,也即是BC1(K) 为了便于对内部平衡点稳定性的讨论,做如下假设: (H3) 其它. 关于内部平衡点的稳定性有如下定理: 定理2 (1)内部平衡点(N*,P*)在τ=0处是局部渐近稳定的. (3)当(H2)成立时,内部平衡点(N*,P*)的稳定性将随着τ的增大而改变有限次,最终变得不稳定. 证明首先定义(N(t),P(t))T: (13) 其中(N*,P*)是系统(1)的唯一的正的内部平衡点.将式(13)带入系统(9)得到: (14) 对式(14)线性化得到: (15) (16) 显然式(16)有非零解当且仅当它的系数矩阵的行列式为零,也就是: (17) 因此可以得到式(15)的特征方程: P(λ)+e-λτQ(λ)=0, (18) 其中P(λ)=λ2+[d-C1(N*)g1′(N*)]λ-dC1(N*)g1′(N*), (19) (20) λ2+a1λ+a0+e-λτ(b1λ+b0)=0 (21) 应用Cooke和Grossman在文献[8]中的引理可以得到: (3)当(H3)成立且τ>0时,方程(21)没有纯虚根. 其中 (22) (23) (24) 现在给定G和ω,把τ做为参数,结合前面的讨论,再应用文献[9]中的引理3可以得到: 对于τ=0的情况,只要满足条件ωK<ω<ωHopf,内部平衡点是局部渐近稳定的.其中ωK的定义见本文式(12), 而: ωHopf=BG-dHopf(G)= 在研究系统平衡点的稳定性时,发现引入时滞的系统存在稳定性开关现象,即当时滞变化经过一序列值时,系统平衡点的稳定性也随之发生变化:从渐进稳定到不稳定,再到渐进稳定,经过有限次循环最后进入不稳定状态.另外,对于平衡点附近的Hopf分支产生的条件及其方向和稳定性,将在以后的文章中给与讨论. [1]Tallamy D W, Rauph M J. Phyto-chemical induction by herbivores[M].New York:New York press USA,1991:201-245. [2]Foley W J, Hume I D.Digestion and energy metabolism in a small arboreal marsupial, the greater glider (Peratauriodes volons) fed high terpene eucalyptus forliage[J].J Comp Phisiol,1987,157(3):355-362. [3]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001. [4]Holling C S.Some characteristics of predation and parasitism[J].Can Ent,1959,91:293-320. [5]Li Y,Feng Z,Swihart R,et al.Modeling plant toxicity on plant-herbivore dynamics[J].J Dynam Differential Equations,2006,18(4):1 021-1 024. [6]Liu R,Feng Z,Zhu H.Bifurcation analysis of a plant-herbivore model with toxin-determined functional response[J].J Differential Equations,2008,245(2):442-467. [7]Liu R,Feng Z,Donald L DeAngelis.Plant-herbivore interactions mediated by plant toxicity[J].Theoretical Population Biology,2008,73(3):449-459. [8]Haukioja F.On the role of plant defenses in fluctuation of herbivore population[J].Oiko S,1980,35:202-213. [9]Wei J,Ruan S.Stability and bifurcation in a neural network model with two delays[J]. Physica D,1999,130(3/4):255-272.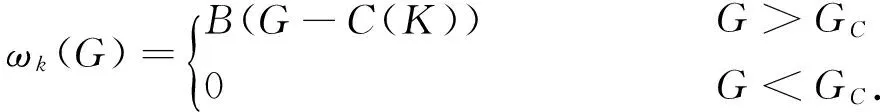
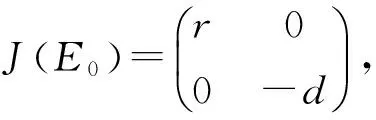
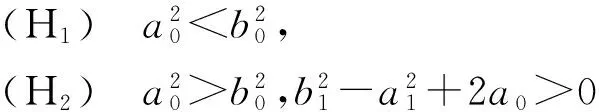
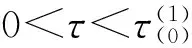
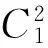
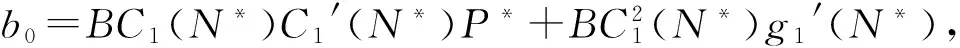
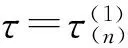
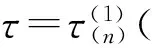

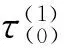
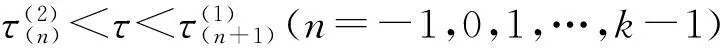
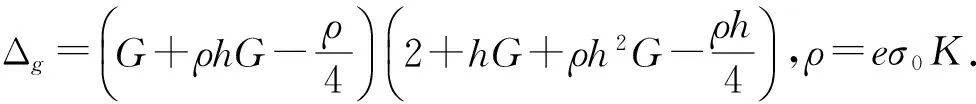
3 结论

