邓肯-张E-μ模型的改进

沈广军

(河海大学岩土工程科学研究所,江苏南京 210098)

邓肯-张E-μ模型的改进

沈广军

(河海大学岩土工程科学研究所,江苏南京 210098)

针对邓肯-张E-μ模型体变经验公式不能准确描述三轴剪切试验体积变形与轴向变形之间关系的问题,首先进行了粗粒土饱和样大型三轴剪切试验,并对试验结果进行了分析,提出了可以准确描述三轴剪切试验体积变形与轴向变形之间关系的体变经验公式,然后利用其他试验数据对该体变经验公式进行了验证,证明了该体变经验公式的通用性,最后基于该体变经验公式对邓肯-张E-μ模型进行了改进,提出了一种新的E-μ模型.

土体;三轴试验;邓肯-张E-μ模型;体变经验公式

随着高土石坝、高速公路、高速铁路等工程的不断兴建,粗粒土的力学性质和本构模型成为岩土工程研究的一个重要课题.从土力学创立以来,已经建立了很多各具特色的本构模型,其中邓肯-张E-μ模型[1]由于形式简单且参数易于确定而在工程中得到了广泛应用.然而,很多试验数据表明,邓肯-张E-μ模型侧向应变-εr与轴向应变εa呈双曲线关系的假定常常并不满足.于是,Daniel等[2-5]提出了一些改进模型(包括Duncan等[5]提出的体积模量代替弹性模量的邓肯E-B模型).笔者通过分析发现,这些改进模型也不能很好地描述实际三轴剪切变形情况.为此,笔者进行了粗粒土饱和样大型三轴剪切试验,并通过对试验结果的分析,提出了可以准确描述三轴剪切试验体积变形与轴向变形之间关系的体变经验公式,在验证了该体变经验公式通用性的基础上,提出了一种改进的E-μ模型.

1 本文体变经验公式的建立

为了研究粗粒土应力与应变之间的关系,笔者采用干密度为2.0g/cm3的砂岩粗粒料进行了饱和样等围压大型三轴排水剪切试验.试验仪器采用河海大学岩土工程科学研究所和长春朝阳仪器厂联合研制的LSW-1000型大型三轴流变仪,试样尺寸为∅300mm×600mm,最大允许粒径60mm,试验结果如图1(a)所示(其中:σ1表示第1主应力;σ3表示第3主应力).

1.1 试验结果规律分析

将试验得到的体积变形 εv与轴向变形εa的关系通过εr=(εv-εa)/2变换成-εr与εa的关系,如图 1(b)所示.从图1(b)可以看出,试验-εr与εa之间并不呈很好的双曲线关系.如果-εr与εa之间呈很好的双曲线关系(即邓肯-张E-μ模型-εr与εa双曲线关系成立),则它们之间的关系可表示为

式中f和D为参数.将式(1)变为

按照式(2),-εr/εa与-εr的关系应为一直线.然而,笔者试验得出的-εr/εa与-εr并不存在很好的线性关系(图1(c)),且f和D的规律性也不是很好.由此可以看出,邓肯-张E-μ模型-εr与εa之间呈双曲线关系的假定存在较大误差.

由于-εr与εa之间的关系用双曲线拟合存在较大误差且参数规律性不是很好、参数不易确定,因此有必要对其进行改进.

笔者经过研究发现,用

可以很好地描述-εr与εa之间的关系.将式(3)变为

式中:f′——直线的截距;D′——直线的斜率.

将体变与轴变的关系变换成-εr/εa与的关系,如图1(d)所示.从图1(d)可以看出,同一围压时的-εr/εa与基本呈直线关系,-εr/εa计算与试验结果误差也较小,一般小于0.03.这说明式(4)能很好地描述试验结果.各围压时-εr与εa关系的拟合效果如图1(e)所示.从图1(e)可以看出,用-εr=f′εa+D′可以很好地描述-εr与εa之间的关系.

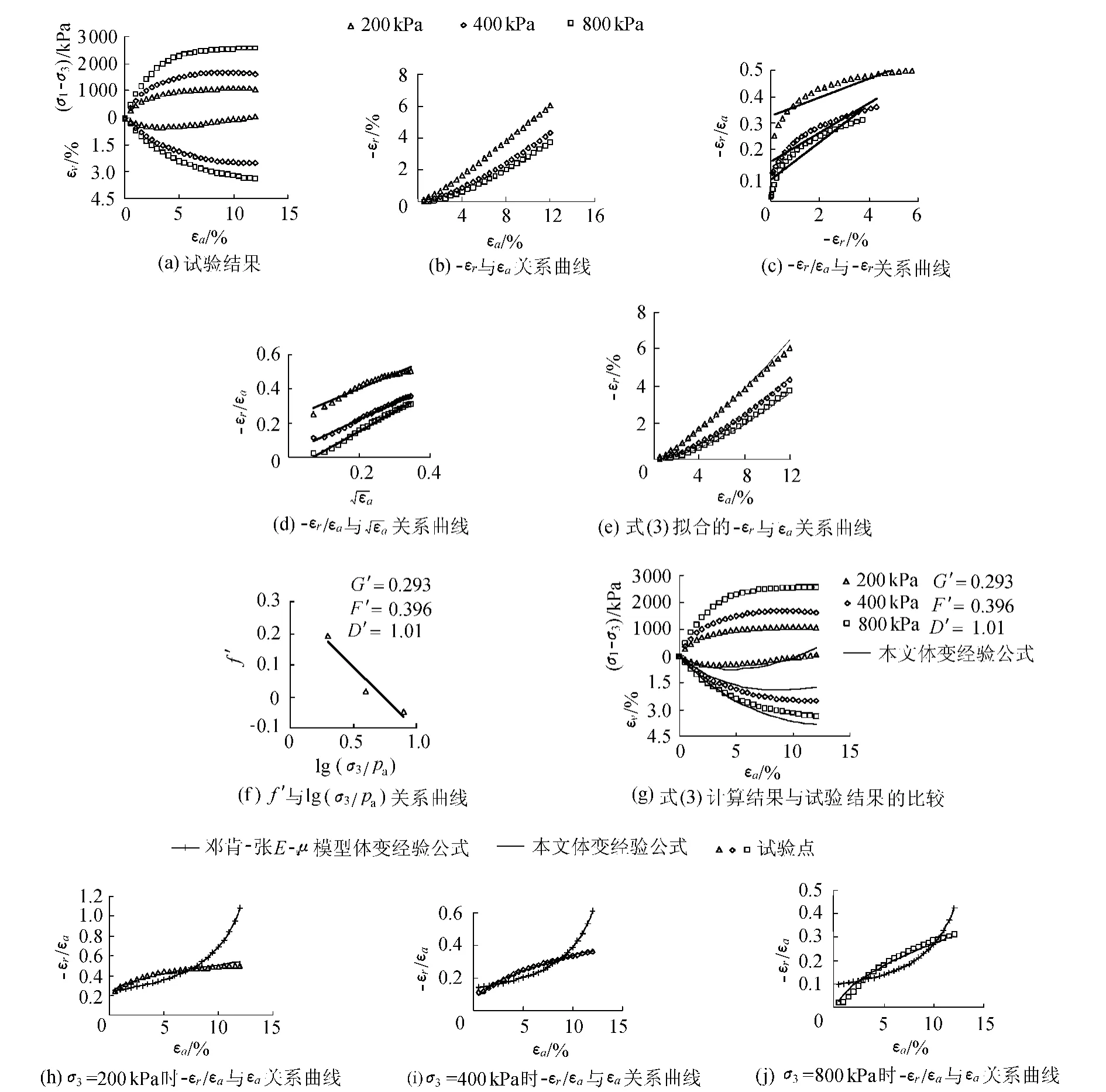
图1 笔者砂岩粗粒料饱和样等围压大型三轴排水剪切试验结果及其分析Fig.1 Results of large-scale triaxial shear tests on saturated samples of coarse-grained sandstone material under same confining pressure

1.2 斜率 D′的确定

从图1(a)可以看出,D′与围压σ3有关,随着σ3的增加而稍有增大,但不同围压之间D′的变化幅度不大,一般取同组试样不同围压下D′的平均值,不会产生太大误差,这里取同组试样不同围压下D′的平均值.

1.3 截距 f′的确定

不同围压下f′与lg(σ3/pa)的关系如图1(f)所示.由图1(f)可以看出,f′与 lg(σ3/pa)呈线性关系,可以表示为

式中:G′,F′——参数;pa——大气压力.

1.4 本文体变经验公式的计算结果

利用式(3)及其参数并根据该试验条件所得计算结果如图1(g)实线所示.从图1(g)可以看出,式(3)能很好地描述实际土体体变规律,能准确地拟合试验结果,能同时准确地描述粗粒土低围压时的剪胀变形和高围压时的剪缩变形.

1.5 2种体变经验公式计算结果的比较

为了对计算结果与试验结果进行比较,将邓肯-张E-μ模型体变经验公式计算结果、本文体变经验公式计算结果和试验结果统一用-εr/εa与εa关系曲线表示,如图1(h),(i),(j)所示.

从图1(i),(j)可以看出:邓肯-张E-μ模型体变经验公式计算得到的-εr/εa在εa较小(即应力水平较小)时偏大,在εa特别大(即应力水平特别大)时明显偏大,而且偏大很多;本文体变经验公式计算结果介于邓肯-张E-μ模型体变经验公式计算结果与试验结果之间,且更贴近试验结果.由此可以看出,本文体变经验公式优于邓肯-张E-μ模型体变经验公式,能更好地描述实际变形规律.

2 本文体变经验公式的验证

为了验证本文体变经验公式的通用性,对50组不同土体的等围压三轴排水、排气剪切试验数据(包括笔者进行的粗粒土风干样和饱和样剪切试验数据,双江口坝壳花岗岩粗粒料风干样、饱和样大型三轴排水(排气)剪切试验数据[6],小浪底堆石料干样、饱和样剪切试验数据[7],干密度为1.45g/cm3的横山坝壳砂砾料饱和样三轴排水剪切试验数据[8],干密度为1.54g/cm3的砂干样、饱和样排水(排气)剪切试验数据[9],三峡二期围堰复合料和垫层料三轴剪切试验数据[10],铁山坝斜墙黏性土三轴排水剪切试验数据[11]等)进行了分析.分析结果表明,本文体变经验公式计算结果与试验结果吻合较好,本文体变经验公式能在较大应变范围内准确描述土体随应力水平增加而变形由体缩向体胀发展的过程,能准确描述粗粒土在低围压下随应力水平增加而先剪缩后剪胀变形、高围压下随应力水平增加而一直剪缩变形,细粒土在低围压下随应力水平增加而一直剪胀变形、高围压下随应力水平增加而一直剪缩变形的过程.由于所有验证结果基本一样,这里仅给出2种验证结果.

2.1 验证结果1

采用干密度为2.078g/cm3的双江口坝壳花岗岩粗粒土饱和样大型三轴排水剪切试验数据(图2(a))[6]对本文体变经验公式进行验证.

将试验数据整理成-εr/εa～关系曲线,如图2(b)所示.从图2(b)可以看出,-εr/εa与呈很好的线性关系.将其表示成-εr/εa=f′+D′,各个围压的D′相差不大,取其平均值D′=1.08.f′随着围压的增加而减小,将f′与lg(σ3/pa)的关系曲线绘出,如图2(c)所示.从图2(c)可以看出,f′与lg(σ3/pa)呈很好的线性关系,据此确定出的G′=0.425,F′=0.348.

利用本文体变经验公式及其参数并根据该试验条件所得计算结果如图2(d)所示.从图2(d)可以看出,本文体变经验公式能很好地拟合试验结果.

图2(e)比较了本文体变经验公式与邓肯-张E-μ模型体变经验公式的拟合效果.从图2(e)可以看出,本文体变经验公式优于邓肯-张E-μ模型体变经验公式.

2.2 验证结果2

采用干密度为1.45g/cm3的横山坝壳砂砾料饱和样三轴排水剪切试验数据(图3(a))[8]对本文体变经验公式进行验证.

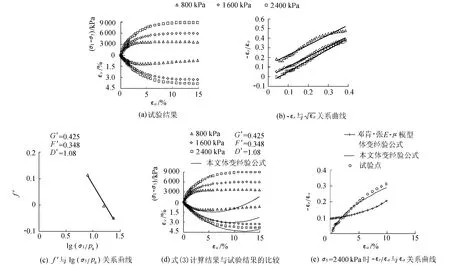
图2 双江口坝壳花岗岩粗粒料饱和样大三轴排水剪切试验数据验证结果Fig.2 Validated results of large-scale triaxial shear tests on saturated samples of coarse-grained granite material of Shuangjiangkou Dam

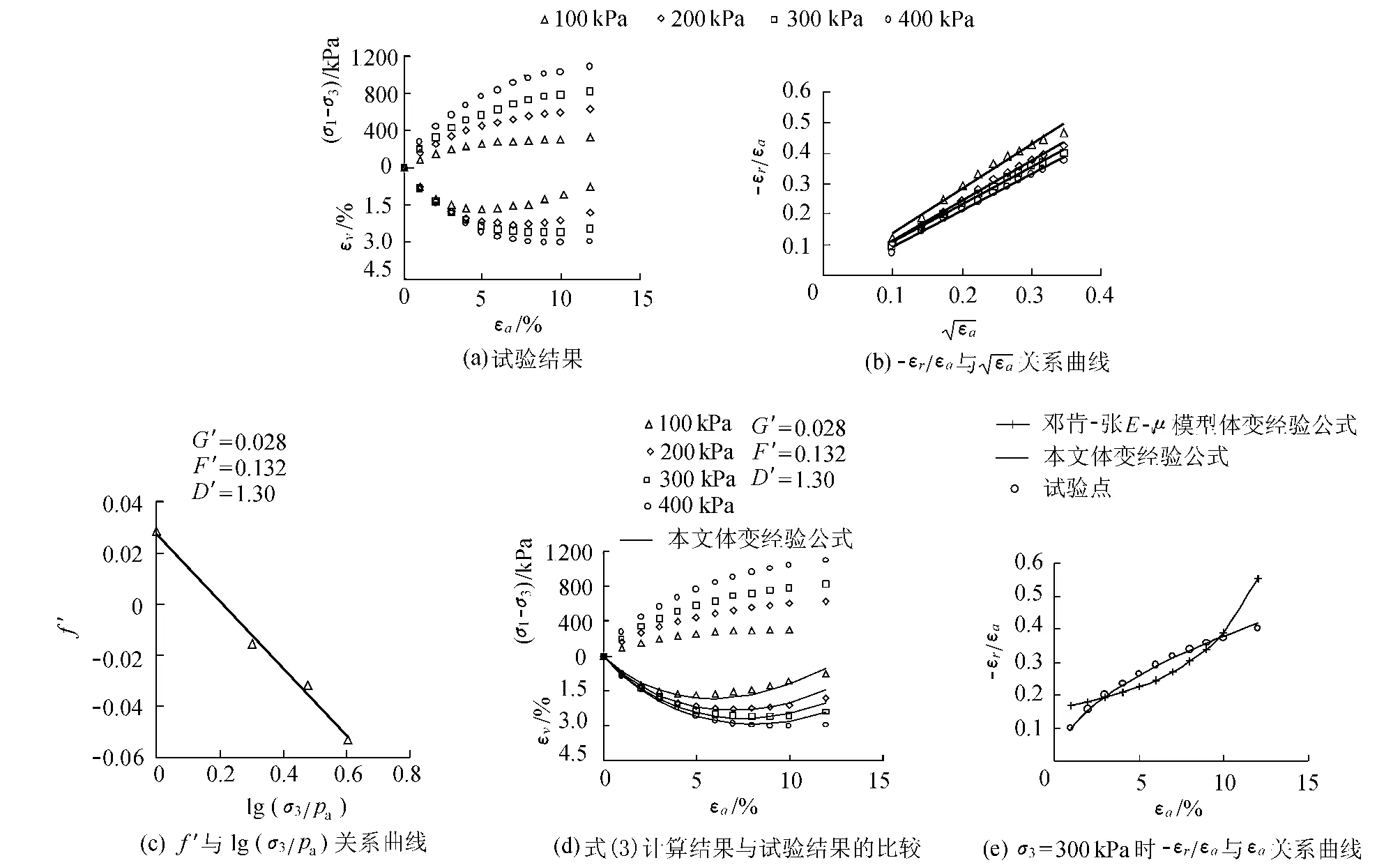
图3 横山坝壳砂砾料饱和样三轴排水剪切试验数据验证结果Fig.3 Validated results of large-scale triaxial shear tests on saturated samples of coarse-grained gravel material of Hengshan Dam

将试验数据整理成-εr/εa～关系曲线,如图3(b)所示.从图3(b)可以看出,-εr/εa与呈很好的线性关系.将其表示成-εr/εa=f′+D′,各个围压的D′相差不大,取其平均值D′=1.30.f′随着围压的增加而减小,将f与lg(σ3/pa)的关系曲线绘出,如图3(c)所示.从图3(c)可以看出,f与 lg(σ3/pa)呈很好的线性关系,据此确定出的G′=0.028,F′=0.132.

利用本文体变经验公式及其参数并根据该试验条件所得计算结果如图3(d)所示.从图3(d)可以看出,本文体变经验公式能很好地拟合试验结果.

图3(e)比较了本文体变经验公式与邓肯-张E-μ模型体变经验公式的拟合效果.从图3(e)可以看出,本文体变经验公式优于邓肯-张E-μ模型体变经验公式.

3 邓肯-张E-μ模型的改进

邓肯-张E-μ模型为

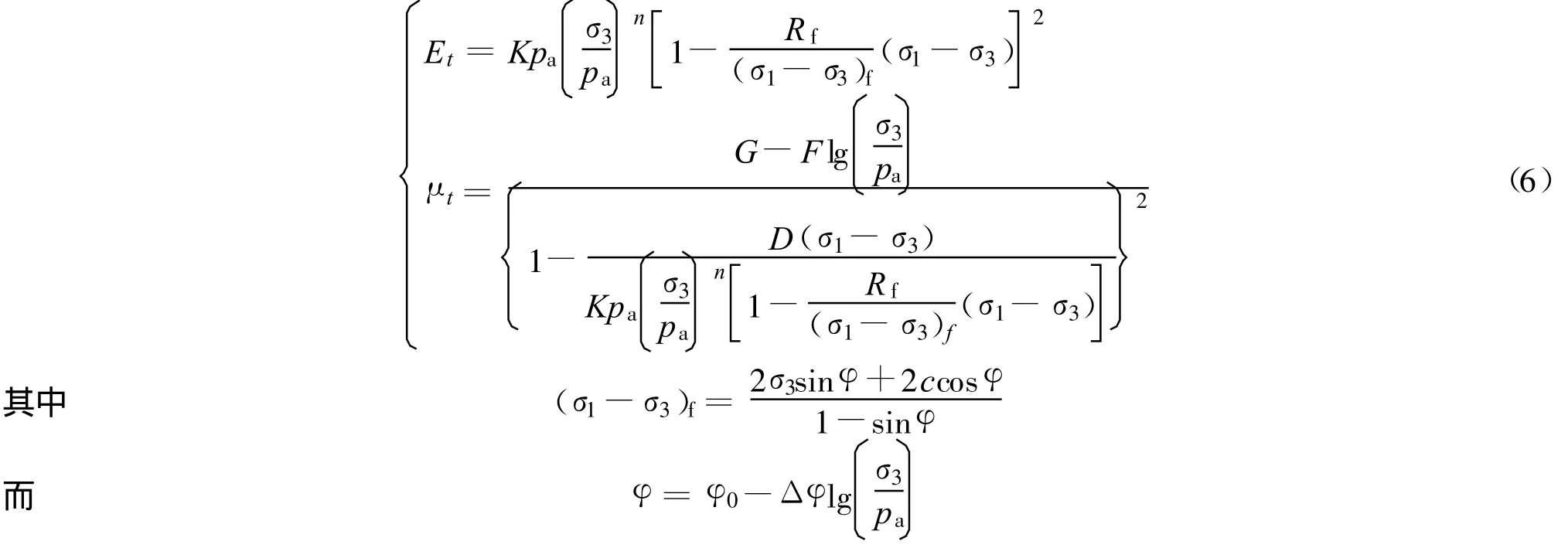
式中:c——黏聚力,非黏性土c=0;φ——摩擦角;φ0,Δφ——计算摩擦角的参数;(σ1-σ3)f——破坏时侧向抗压强度;Rf——破坏比;K,n,G,F,D——试验常数.该模型主要参数c,φ(或 φ0,Δφ),Rf,K,n,G,F和D可通过三轴剪切试验确定.

依据本文所提出的体变经验公式_对邓肯-张E-μ模型体变_经验公式进行改进,则可得到改进的E-μ模型

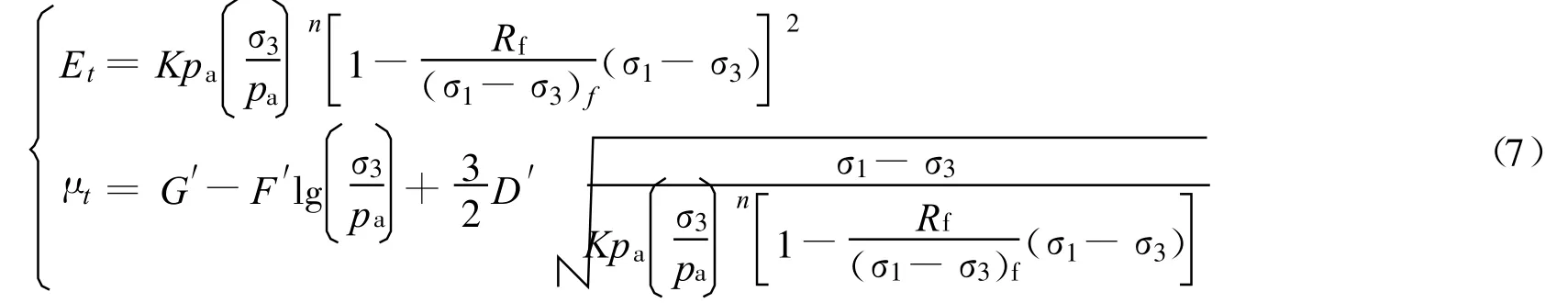
式中G′,F′,D′为试验常数.由于虎克定律不能反映剪胀性,因此有必要限制 μt的取值范围,故令 μt≤0.49.

4 结 论

a.本文分析得出的等围压三轴排水剪切试验-εr与εa呈-εr=f′εa+关系的结果对很多土体都非常适用.

b.体变参量f′和D′规律性很好,且易于准确确定.

c.利用本文体变经验公式及其参数预测得到的三轴排水剪切试验条件下的试验结果与实际试验结果吻合很好.

d.本文所提出的体变经验公式明显优于邓肯-张E-μ模型体变经验公式.

e.与邓肯-张E-μ模型相比,改进的E-μ模型参数更易准确确定,拟合效果更好.

[1]DUNCAN J M,CHANG C Y.Nonlinear analysis of stress and strain in soils[J].Journal of the Soil Mechanics and Foundations Division,ASCE,1970,96(5):1629-1653.

[2]DANIEL D E,OLSON R E.Stress-strain properties of compacted clays[J].Journal of the Geotechnical Engineering Division,ASCE,1974,100(10):1123-1136.

[3]沈珠江.考虑剪胀性的土和石料的非线性应力应变模式[J].水利水运科学研究,1986(4):1-14.(SHEN Zhu-jiang.A nonlinear dilatant stress-strain mode for soil and rock materials[J].Hydro-science and Engineering,1986(4):1-14.(in Chinese))

[4]司洪洋.确定土石坝坝壳料邓肯模型参数的几个问题[J].水力发电,1983(8):31-35.(SI Hong-yang.Several problems of determining the earth and rockfill dam parameter of duncan model[J].Water Power,1983(8):31-35.(in Chinese))

[5]DUNCAN J M,BYRNE P,WONG K S,et al.Strength,tress-strain and bulk modulus parameters for FEA of stress and movements in soil masses,Report No.UCB/GT/80-01[R].California:California University,1980.

[6]左永振.粗粒料的蠕变和湿化试验研究[D].武汉:长江科学院,2008.

[7]李广信.干、湿状态的小浪底土坝堆石料的三轴试验研究[R].北京:清华大学,1988.

[8]沈珠江,王剑平.横山水库土石坝有效应力应变分析[J].水利学报,1990(4):59-65.(SHEN Zhu-jiang,WANG Jian-ping.Effective stress and strain analysis of Hengsan reservoir earth-rock dam[J].Journal of Hydraulic Engineering,1990(4):59-65.(in Chinese))

[9]沈珠江,左元明.坝壳砂砾料的浸水变形特性的测定[R].南京:南京水利科学研究院,1986.

[10]张嘎,张建民.粗颗粒土的应力应变特性及其数学描述研究[J].岩土力学,2004,25(10):1587-1591.(ZHANG Ga,ZHANG Jian-min.Study on behavior of coarse grained soil and its modeling[J].Rock and Soil Mechanics,2004,25(10):1587-1591.(in Chinese))

[11]谢晓华,沈珠江.土石坝计算中非线性模型的改进[J].水利水运工程学报,1988(3):43-55.(XIE Xiao-hua,SHEN Zhu-jiang.Modification of nonlinear model in the stress-strain analysis of earth and rockfill dam[J].Hydro-science and Engineering,1988(3):43-55.(in Chinese))

Improvement of Duncan-ChangE-μmodel

SHEN Guang-jun
(Geotechnical Research Institute of Hohai University,Nanjing210098,China)

Since the empirical formula of volumetric deformation of the Duncan-ChangE-μmodel cannot accurately depict the relationship between the volumetric and axial deformation of the triaxial shear tests,large-scale triaxial shear tests on saturated samples of coarse-grained soils were carried out.The test results were analyzed.An empirical formula of volumetric deformation that can accurately depict the relationship between the volumetric and axial deformation of the triaxial shear tests was proposed.The proposed empirical formula was validated using other researchers'test data.Its universality was proved.Based on the proposed empirical formula of volumetric deformation,a newE-μmodel that is an improvement of the Duncan-ChangE-μ model is presented.

soil;triaxial test;Duncan-ChangE-μmodel;empirical formula of volumetric deformation

TU411.3

A

1000-1980(2010)01-0109-06

10.3876/j.issn.1000-1980.2010.01.023

2009-09-05

沈广军(1979—),男,江苏扬州人,博士研究生,主要从事岩土材料特性和数值模拟研究.E-mail:shen_gj@sina.com.cn