用神经网络技术确定枇杷叶中熊果酸提取时间*

孙益民，焦容容，孙若琼，张继红

1(安徽省功能性分子固体重点实验室，安徽芜湖，241000) 2(安徽师范大学化学与材料科学学院，安徽芜湖，241000)3(安徽师范大学生命科学学院，安徽芜湖，241000) 4(安徽师范大学环境科学学院，安徽芜湖，241000)5(安徽省天然产物超临界提取工程技术研究中心，安徽芜湖，241007)

熊果酸(ursolic acid)是枇杷叶的有效成分之一，又名乌苏酸、乌索酸，是多种植物的功能成分，具有抗炎抗菌、抗肝损伤［1－2］、抗氧化［3］、降血糖、降血脂、止咳等多种药理活性［4］。近年来又发现熊果酸是很好的免疫增强剂［5］，具有较显著的免疫和抗致癌作用。同时，熊果酸及其衍物还对病毒具有抑制活性，可望成为低毒、有效的新型抗癌和抗爱滋病毒药物［6］。日本专利显示熊果酸在抗癌保健食品、饮料和护发素、头发生长剂等方面也有一定的应用［7］。可见，熊果酸有着广阔的应用前景和十分重要的开发利用价值。

目前，对熊果酸提取多采用溶剂提取法。其特点是操作简单，成本低廉。作者曾对超声波辅助提取熊果酸进行较为系统的研究，运用均匀设计法安排试验［8－9］，以高效液相色谱测定熊果酸的含量，以提取率为试验指标，研究了乙醇体积分数、提取时间、提取次数、液固比及粒子大小5个因素对提取效果的影响。本文针对提取时间的影响进行了重点研究。

均匀设计可以安排多因素多水平试验，均匀试验成功关键在于科学合理地建立试验因素与试验指标间的定量关系，对实验体系进行描述，从而进行工艺优化［10］。本文应用人工神经网络技术挖掘试验信息，并进行仿真指导验证试验，最终获得了提取熊果酸的优化工艺，为工业化生产提供可靠参考信息。

1 实验部分

1.1 主要试剂与仪器

枇杷叶采自安徽芜湖，经鉴定为蔷薇科植物枇杷Eriobotrya japonica(Thunb.)Lindl.的叶。无水乙醇(AR)，石油醚(AR、沸点60～90℃):国药集团化学试剂有限公司;NaOH(AR):汕头市西陇化工厂有限公司;熊果酸标准品:安徽芜湖甙尔塔医药科技有限公司。

FA1204电子天平，上海民桥精密科学仪器有限公司;WG-43电热鼓风干燥机，天津市泰斯特仪器有限公司;WF-111型高速中药粉碎机，江阴市新友机械制造有限公司;TG328B分析天平，上海良平仪器仪表有限公司;RE-52AA旋转蒸发仪，上海振捷实验设备有限公司;CQ-150超声波清洗机，上海跃进医用光学器械厂;美国Mode12000半制备色谱仪(配有Lab Alliance model 500可变波长紫外检测器和Lab Alliance HPLC Workstation)，美国Science System公司。

1.2 实验方法

1.2.1 用超声波法提取枇杷叶中熊果酸

将枇杷叶洗净、去毛后放在干燥箱中烘干，冷却至室温后经粉碎机粉碎，经过分样筛后备用。

称取一定量的枇杷叶粉，超声提取，趁热过滤，滤液经旋转蒸发浓缩后，以石油醚萃取近无色，萃余物配成无水乙醇溶液，加入适量的稀NaOH溶液，调节pH值至10～11，静置。再将所得滤液中加入适量稀HCl，调节pH值至2～3。然后加入一定量蒸馏水，离心分离，干燥即得熊果酸粗品。

1.2.2 高效液相色谱测定所得粗品中熊果酸的含量

1.2.2.1 色谱条件

色谱柱为Column型C18柱(4.6 mm×250 mm，5 μm);流动相为 V(甲醇)∶V(水)=97∶3;检测波长:215 nm;流速0.8 mL/min;柱温13℃。

1.2.2.2 标准曲线的绘制

精密称取熊果酸标准品5.3 mg置于10 mL容量瓶中，以甲醇定容，得到530 μg/mL的标准品溶液。再依次稀释得 106、21.2、10.6、5.3 μg/mL 熊果酸对照品溶液。分别准确吸取熊果酸对照品溶液，在1.2.2.1色谱条件下进样20 μL进行测定。其峰面积和浓度呈线性相关。回归方程为Y=6 799+4 928X，r=0.999 999。

式中:Y为峰面积，X为浓度，r为相关因数。

说明当熊果酸进样量在5.3～106 μg/mL时，线性关系良好。

1.2.2.3 原料溶液的制备

精密称取干燥枇杷叶粉末5.049 6 g，加入30 mL甲醇超声3次，每次30 min，合并提取液，过滤，甲醇定容至100 mL容量瓶，摇匀，取上清液，用孔径为0.45 μm 的微孔滤膜过滤，进样量20 μL，采用高效液相色谱法分析，得原料中熊果酸含量为1.042%。

1.2.2.4 粗品溶液的制备

精密称取一定量的熊果酸粗品，甲醇定容至50 mL容量瓶中，摇匀，取上清液，用孔径为0.45 μm的微孔滤膜过滤，进样量20 μL，采用高效液相色谱法分析，归一法测定粗品中熊果酸的含量，并分别计算出各个试验的提取率。

2 结果与讨论

2.1 均匀试验设计与结果

取20g枇杷叶粉末，乙醇为溶剂，超声提取。用均匀设计法考察了乙醇体积分数、提取时间、提取次数、液固比以及粒子大小对提取效果的影响。以提取率为试验评价指标，试验安排与结果如表1所示。

从表1可以看出，均匀设计试验的结果没有整齐可比性，大多数文献报道试验结果通常用多因素多水平线性回归分析或逐步回归分析的方法来筛选变量，建立定量关系［11］。然而提取率与提取工艺条件之间是一种复杂非线性关系，提取条件间存在交互影响，如果工艺条件多结果分析很难做到科学合理。而人工神经网络作为人工智能的一种计算工具，能够有效地考察提取条件间的交互作用，具有强大的处理非线性问题的能力［12］。本文用人工神经网络技术研究试验结果、分析系统规律。

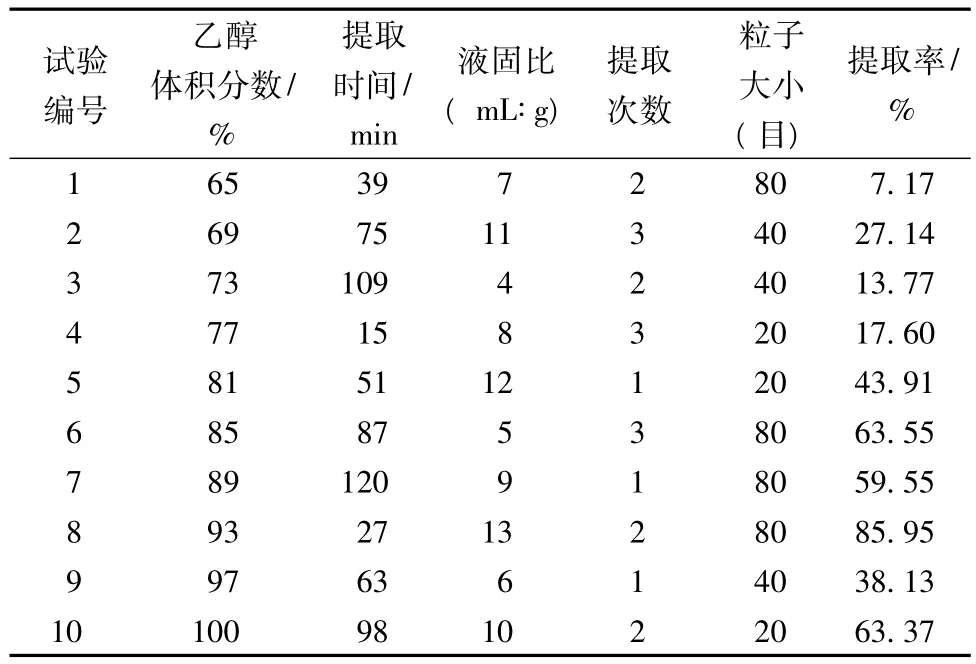
表1 均匀设计试验与结果

2.2 人工神经网络建模

2.2.1 人工神经网络模型的建立

对试验数据采用3层的拓扑结构为5－3－1的误差反向传播模型(back-propagation，BP)建立描述熊果酸提取的人工神经网络辨识模型。网络输入层的节点数即为工艺中影响因素的数量，试验为5个影响因素因此有5个输入节点。网络输出层的节点数是试验评价指标即提取率指标，亦即优化工艺预报的对象。本工作的输出节点数为1。为了保证模型的健壮性，本文中隐藏层的节点数经过反复试验计算，确定其数量为3，此数值较小建立的模型健壮性强。

2.2.2 人工神经网络模型参数的确定

BP网络具有学习功能，每次以随机抽取的8(=10－2)组试验数据进行训练，其余2组试验数据用作测试模型质量，称为“留二法”(leave-two-out)，在训练过程中可以根据计算误差调整权重，当误差达到10－6时，记录当前权重值和偏置值，构成模型网络，训练次数为29次，训练误差见图1。网络参数如表2、表3所示。

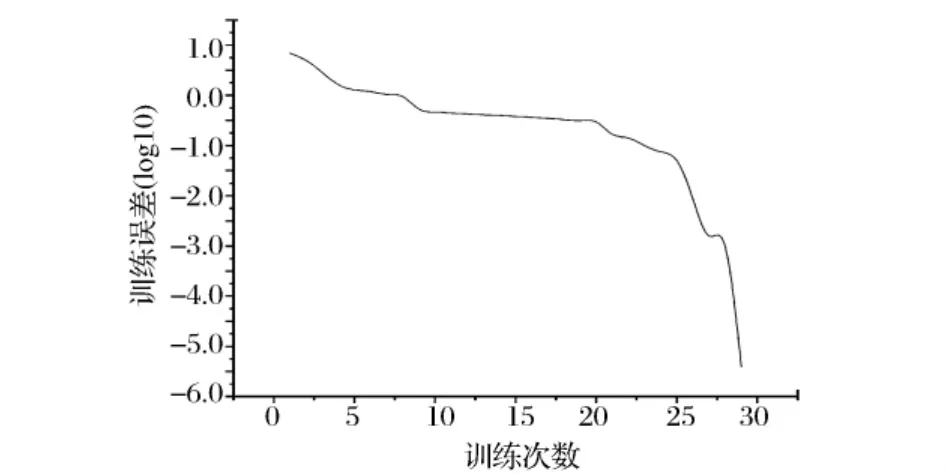
图1 网络模型训练误差

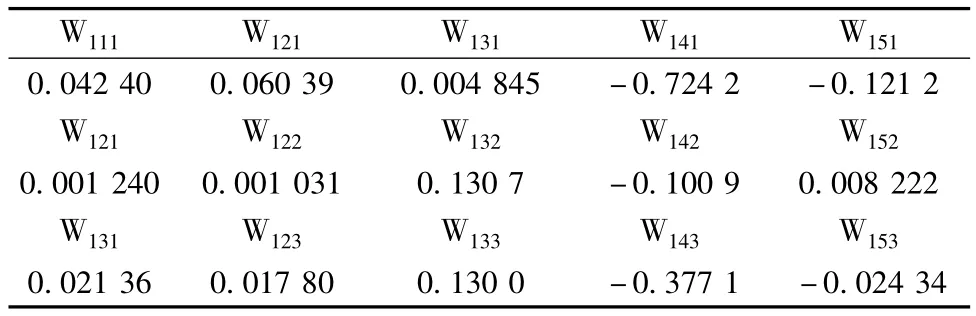
表2 隐含层与输入层的连接权重

表3 输出层与隐含层的连接权重和偏置

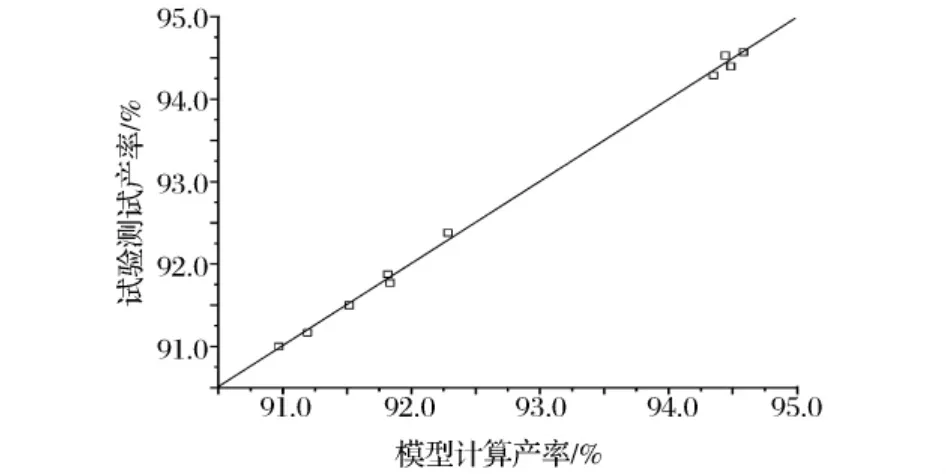
图2 模型计算值与试验值比较

2.2.3 人工神经网络模型的试验验证

为了检验人工神经网络建模结果的可靠性，用验证试验对人工神经网络模型进行验证。

表4 验证试验值与计算值比较

表4给出了试验测定值与神经网络辨识值。图2横坐标为神经网络辨识值，纵坐标为试验测定值，各点越接近对角线就说明两者误差越小。如图2所示，训练预报点和试验点大部分散落在对角线附近，误差较小，验证了人工神经网络模型系统辨识结果的可靠性。

2.3 提取熊果酸时间特性研究

为了使试验更加符合实际情况，更快寻找出优化工艺，采用多因素多水平邻近分析的方法对枇杷叶中熊果酸的提取工艺进行研究，即以均匀试验的各组参数为基础，利用已训练成功的人工神经网络模型对试验点附近的参数组合进行较为系统的研究。此种方法高度保持了均匀试验设计的“均匀”特性，使得研究工艺范围广，研究范例具有均匀性、系统性。

由于需要系统研究的工艺范围广泛，涉及参数众多，限于篇幅原因，本文论述的只是不同乙醇体积分数条件下提取时间对产率影响。在相应试验工艺条件下研究其影响规律，通过神经网络模型指导安排新的试验。

2.3.1 试验1与试验2邻近时间影响分析

图3 液固比7∶1(g∶mL)，提取2次，粒子80目时不同乙醇体积分数下提取时间对产率的影响

图3 可以看出7条曲线的变化趋势基本一致，随着提取时间的延长，熊果酸提取率都为增长的趋势。不同乙醇体积分数条件下，提取时间的延长对产率影响不同。乙醇体积分数在低浓度65%时，随着提取时间的延长，产率增加幅度不大，时间延长到95 min时产率达到最大极限值94.98%。同时随着乙醇体积分数的增大，产率达极限值需要的提取时间在缩短。乙醇体积分数在较低浓度80%时，延长到75 min时产率达到最大极限值95%左右。在试验1条件下，若提取时间小于60 min，则同一提取时间下，乙醇体积分数越高，熊果酸提取率就越高。从提取时间-产率关系上分析，试验1工艺时间特性属于“加速型”，即延长提取时间产率的增长率提高。

图4 液固比11∶1(g∶mL)，提取3次，粒子大小40目不同乙醇体积分数下提取时间对产率的影响

由图4可见，随着提取时间的延长产率先减少后增加，减小的速度明显比增加的速度快，并且增加的幅度很小，产品产率较低。提取时间的延长对低浓度乙醇条件下的产率影响较大。乙醇体积分数为65%时，随着提取时间的延长产率变化很明显，提取时间在60 min时产率大于90%，延长时间到90 min时产率10.18%，90 min后提取率缓慢上升。延长时间到90 min以上时乙醇体积分数越高产率越高。从提取时间-产率关系上分析，试验2工艺时间特性属于“抛物线型”，即提取时间对产率的影响有极低值。

2.3.2 试验3与试验4邻近时间影响分析

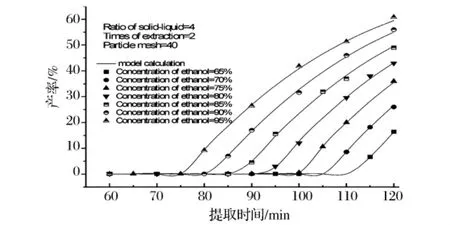
图5 液固比4∶1(mL∶g)，提取2次，粒子大小40目时不同乙醇体积分数下提取时间对产率的影响

图5 中曲线变化趋势基本一致，随着提取时间的不断延长，熊果酸的提取率不断增大。在乙醇体积分数较低的情况下，增加提取时间，产品产率的增加不明显。这种趋势在65%乙醇体积分数下提取熊果酸表现的更为明显，提取时间从60 min变化到110 min时，产率仅为最低极限0.086%。随着乙醇体积分数的不断增大，提取时间对产率的影响较为明显，当乙醇体积分数达到95%时，提取时间延长至80 min以后，提取率快速上升。从提取时间-产率关系上分析，试验3工艺时间特性属于“减速型”，即延长提取时间产率的增长率降低。

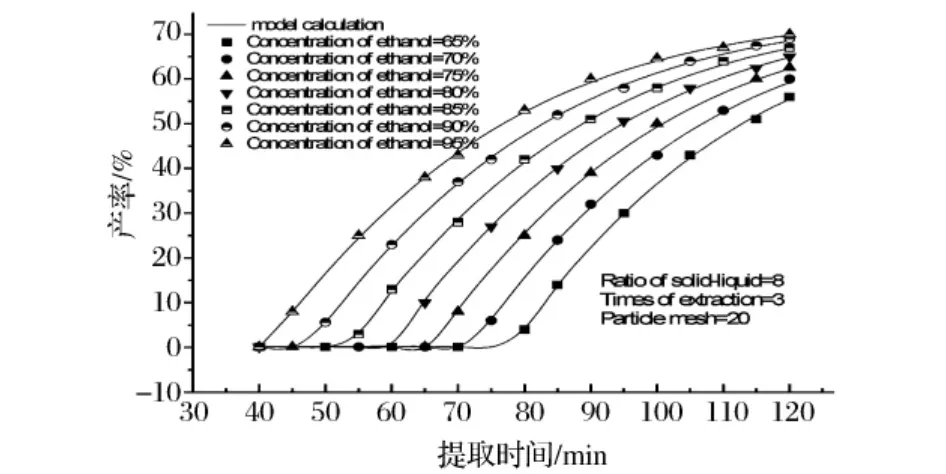
图6 液固比8∶1，提取3次，粒子大小20目不同乙醇体积分数下提取时间对产率的影响

从图6可得到同样的规律:随着提取时间的延长，熊果酸的提取率不断增大而且变化幅度比较大。不同乙醇体积分数条件下要得到同样产率的产品所需提取时间不同。乙醇体积分数为65%时，产率要高于40%至少要提取105 min，乙醇体积分数75%时需要95 min，乙醇体积分数90%时至多需要75 min。从提取时间-产率关系上分析，试验4工艺时间特性与试验3相同属于“减速型”。

2.3.3 试验5与试验6邻近时间影响分析

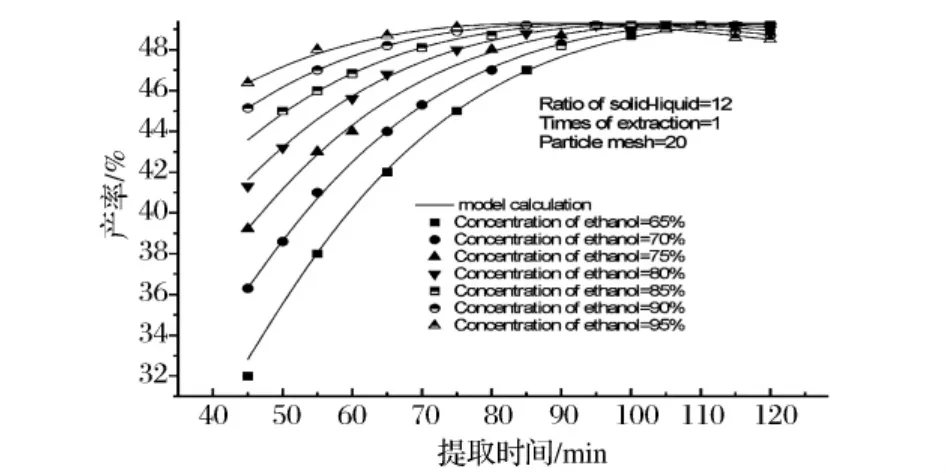
图7 液固比12∶1，提取1次，粒子大小20目时不同乙醇体积分数下提取时间对产率的影响

从图7可见，提取时间的延长对熊果酸提取率的影响不同。乙醇体积分数为65%时，产率随提取时间的增加而增加。随着乙醇体积分数的增大，产率随提取时间的增加幅度不断减小，最终出现不明显的提取率降低趋势。低乙醇体积分数产率增加幅度大，提取时间从60～80 min的20 min内65%乙醇产率提高0.29%/min，85%乙醇产率则提高0.09%/min。从提取时间-产率关系上分析，试验5工艺时间特性亦属于“减速型”。

图8 液固比5∶1，提取3次，粒子大小80目时不同乙醇体积分数下提取时间对产率的影响

图8 中曲线变化的整体趋势是延长提取时间有利于提高熊果酸提取率。若要得到产率在90%以上的产品，90%的乙醇中要提取95 min，80%的乙醇中则要提取110 min，当乙醇体积分数降到70%时，提取120 min，仅得到不足85%的产率。从提取时间-产率关系上分析，试验6工艺时间特性属于“加速型”。

2.3.4 试验7与试验8邻近时间影响分析

图9 液固比9∶1，提取1次，粒子大小80目时不同乙醇体积分数下提取时间对产率的影响

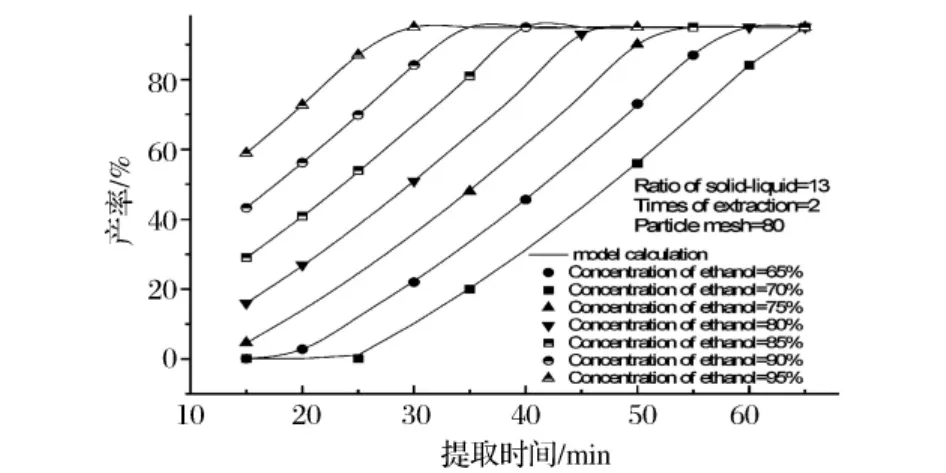
图10 液固比13∶1，提取2次，粒子大小80目时不同乙醇体积分数下提取时间对产率的影响

从图9可见，延长提取时间并不利于熊果酸提取率的提高。较低乙醇体积分数条件下，产率并没有随着提取时间的延长而变化;较高乙醇体积分数条件下，产率随着提取时间的延长反而在降低，下降的幅度较大。若提取时间从105 min延长到120 min，乙醇体积分数为90%时，产率降低了近40%;乙醇体积分数为85%时，产率降低了近25%。因此，在较低乙醇体积分数条件下，105 min时就能得到高产率的产品。从提取时间-产率关系上分析，试验7工艺时间特性为“衰减型”，即延长提取时间产率降低较快。

图10可以看出延长提取时间有利于提高熊果酸提取率。不同乙醇体积分数条件下，延长提取时间对熊果酸提取率影响不同。提取时间为25 min时，乙醇体积分数为65%的提取条件下，产率只有1.10%;乙醇体积分数为80%的产率为38.33%;乙醇体积分数为95%的产率为87.05%;要得到高产率的产品，乙醇体积分数为95%的提取条件下只需延长5 min即得到94.98%的产率，乙醇体积分数为80%的需延长20 min方可得到同产率产品，而乙醇体积分数为65%的则要延长30 min。从提取时间-产率关系上分析，试验8工艺时间特性属于“加速型”。

2.3.5 试验9与试验10邻近时间影响分析

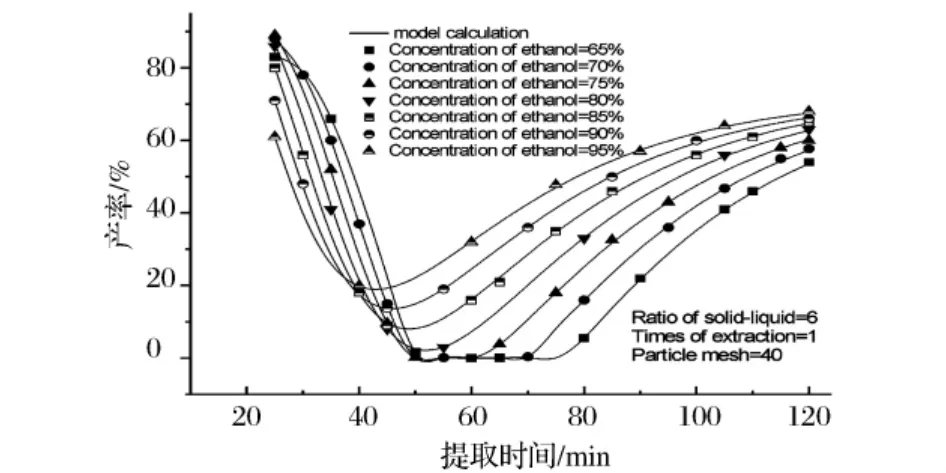
图11 液固比6∶1，提取1次，粒子大小40目时不同乙醇体积分数下提取时间对产率的影响

图12 液固比10∶1，提取2次，粒子大小20目时不同乙醇体积分数下提取时间对产率的影响

可以看出图11中曲线的变化与图4中曲线变化基本一致，随着提取时间的延长产率先减少后增加，减小的速度明显比增加的速度快，并且增加的幅度很小，较低乙醇体积分数提取条件下产品产率低于其相应的初始值。提取时间的延长对低浓度乙醇条件下的产率影响较大。乙醇体积分数为65%时，随着提取时间的延长产率变化很明显，提取时间在25 min时产率大于90%，延长时间产率降低，达到最低值后，时间的延长有利于产率的提高。从提取时间-产率关系上分析，试验9工艺时间特性属于“抛物线型”。

从图12可见，曲线变化趋势一致，延长提取时间有利于提高熊果酸的提取率。不同乙醇体积分数条件下，提取时间的延长对熊果酸提取率的影响是不同的。乙醇体积分数较低时，提取率随时间的延长增加较快;乙醇体积分数较高时，提取率随提取时间的延长增加缓慢。提取相同的时间，乙醇体积分数越高，熊果酸的提取率就越高。从提取时间-产率关系上分析，试验10工艺时间特性与试验3相同属于“减速型”。

2.3.6 时间影响分析

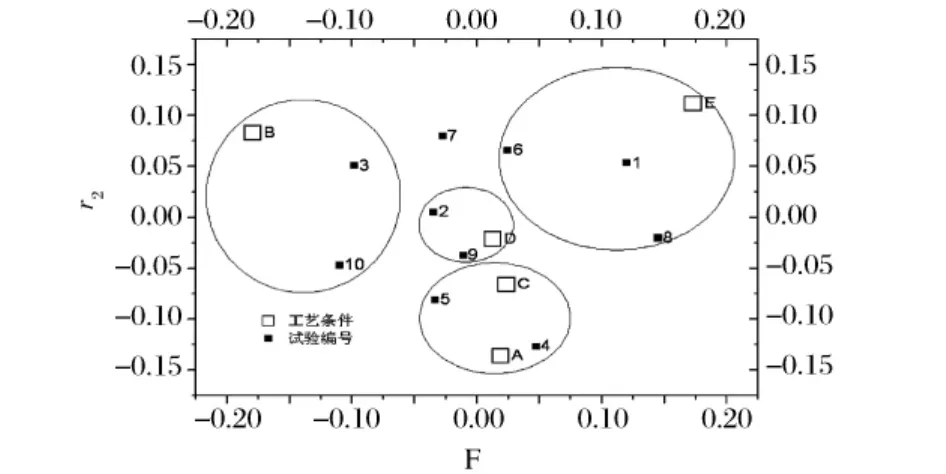
图13 对应因子分析时间特性影响工艺分类

采用对应因子分析方法［13］对10个试验的时间特性进行分析，可以发现其基本规律。对应因子分析坐标 F1=6.321 944×10－2乙醇体积分数(%)+7.569 224×10－2提取时间(min) －7.135 487×10－1液固比(mL/g)+9.362 540×10－2提取次数 +5.111 274×10－2粒子大小(目)+6.882 883 ×10－1提取率(%)

F2=4.270 738×10－2乙醇体积分数(%)－6.612 222×10－1提取时间(min)+3.991 259 ×10－1液固比( mL/g)－3.209 876×10－1提取次数－1.051 221×10－1粒子大小(目)+5.379 590 ×10－1提取率(%)

图13中A、B、C、D和E分别依次表示乙醇体积分数、提取时间、液固比、提取次数和粒子大小。图13可见。试验1、6、8基本属于一类，其时间特性为“加速型”，即随着时间推移提取效率增率提高，且相近原因是粒子大小均为80目，导致“加速型”影响关系。试验3、10相近由于提取时间相近，试验4、5相近由于乙醇体积分数和液固比原因，这4个试验呈“减速型”特性，即随着时间推移提取效率增率降低。试验2、9划为一类，呈现“抛物线型”，即随着时间推移提取效率先降低再升高。7属于另类，“衰减型”，即随着时间推移提取效率降低。

3 工艺优化

利用训练成功的人工神经网络模型优化了枇杷叶中熊果酸提取工艺参数，结果如表6所示。

以产率高于90%为目标优化，提取时间间隔15 min，在考察各影响因素试验范围区间内，共发现307组工艺组合，现列出其中的26组。

表6 产率在91%～99%产品生产工艺部分优化结果(共307组，列出低浓度段26组供参考)

选取表6中的乙醇体积分数为65%，提取时间为15 min，液固比为10，提取次数为2，颗粒目数为40目，做试验，产率为90.77%(模型计算为91.38%)。

4 结论

采用均匀设计法安排试验，其特点研究因素多，研究水平数多，有利于系统研究。采用人工神经网络高度非线性分析技术能够解决多因素多水平试验结果建模问题。本文提出的多因素多水平邻近分析方法将巨大量的试验结果分析合理简化，取得了很好的效果。其优化的工艺经过试验验证基本一致。

［1］ Saraswat B，Visen P K，Agarwal D P.Ursolic acid isolated from Eucalyptus tereticornis protects against ethanol toxicity in isolated rat hepatocytes［J］.Phytother Res，2000，14(3):163－166.

［2］ Miura N，Matsumoto Y，Miyairi S，et al.Protective effects of triterpene compounds against the cytotoxicity of cadmium in HepG2 cells［J］.Mol Pharmacol，1999，56(6):1 324－1 328.

［3］ Somova L I，Shode F O，Ramnanan P，et al.Antihypertensive，antiatherosclerotic and antioxidant activity of triterpenoids isolated from Olea europaea，subspecies Africana leaves［J］.Journal of Ethnopharmacology，2003，84:299－305.

［4］ 刘传安，邹盛勤，陈武.枇杷叶化学成分、药理作用及其应用研究进展［J］.安徽农业科学，2005，33(11):2 117－2 118.

［5］ You H J，Choi C Y，Kim J Y，et al.Ursolic acid enhances nitric oxide and tumor necrosis factor-alpha production via nuclear factor-kappaB activation in the resting macrophages［J］.FEBS Lett，2001，509(2):156 － 160.

［6］ 黄镜，孙燕.熊果酸的抗肿瘤活性［J］.中国新药杂志，1997，6(2):101－104.

［7］ 韩小龙.从枇杷叶中提取分离熊果酸的工艺研究［D］.西安:西北大学:2005.

［8］ 罗乐，孙益民，宋文佳，等.可视分析法在辣椒籽油提取工艺优化中的应用研究［J］.食品科技，2008，33(12):155－161.

［9］ 宋文佳，孙益民，罗乐，等.辣椒红色素提取工艺的可视化分析［J］.应用化工，2008，37(7):743－750.

［10］ 蒋益虹.荷叶黄酮的乙醇提取工艺优化研究［J］.农业工程学报，2004，20(4):168－171.

［11］ 毛东森.均匀设计及其在化学化工中的应用［J］.化工进展，1997(5):16－19.

［12］ 方柏山.生物技术过程模型化与控制［M］.广州:暨南大学出版社，1997.

［13］ 曾道明，纪宏金，高文，等.R－Q型因子分析与对应分析［J］.物探化探计算技术，2008:30(1)，78－80.