用确定流速分布的方法解决大管道气体流量计量问题

殷兴景,熊玉亭,苏中地

(1.浙江苍南仪表厂,浙江苍南 325800;2.中国计量学院计量测试工程学院,杭州 310018)

0 引 言

近年来,很多大管道气体流量检测仪表采用的原理是速度面积法,即仅测取管道中一点或多点的流速来推算管道流量,安装形式为插入式。这类仪表的共同特点:结构简单、安装维修方便、价格低廉和重复性好,是工控系统中检测大管道气体流量性价比较高的仪表[1]。在管道口径(大于300 mm)时,均速管流量计压损小、节能、结构简单和拆装方便等优势更加明显。

均速管流量计是基于早期皮托管(Pitot)测速原理发展起来的,它是以测管道中直径(圆管)或长与宽(矩形管)上几点的流速来推算流量的一种插入式流量仪表。

在国内倡导建设节约型社会的前提下,均速管流量计被广泛运用于大口径、大流量气体介质管道的测量中。西气东输工程中,在内径为1 000 mm的干线管道上,选用了50台均速管流量计,占总量的52%[2]。此外,均速管流量计在国内电力、冶金、石化等行业中,也得到广泛应用。

针对均速管流量计输出差压小、精确度低,忽视管内径对精确度的影响等缺点推出的一项专利产品——均速环流量计。它由双文丘里管测低压,提高了输出差压,用多根均速管充分反映了管内的流速分布等一系列措施,改善均速管的技术特性,已引起国内外厂商及用户的关注[3]。

1 方法分析

笔者建议,在可能的情况下,针对不同管道的特定截面使用精度较高的流速计测量其速度分布曲线及一定流速范围内的速度分布曲线的变化趋势,就可以根据速度分布公式推出该面的速度分布情况,最后通过速度面积法得出流量。

对于圆管内速度分布式的研究,最经典且最常用的是Nikaradse于1932年提出的指数分布模型(如图1所示)。v是管道截面上一点的流速;r代表管道内相对于中心轴线的位移;R代表管道半径,则v和r在理论上满足公式:

式中 vmax——管道中心处的最大速度,vmax=——管内平均流速,n——指数,随雷诺数 ReD变化的常数[4]。

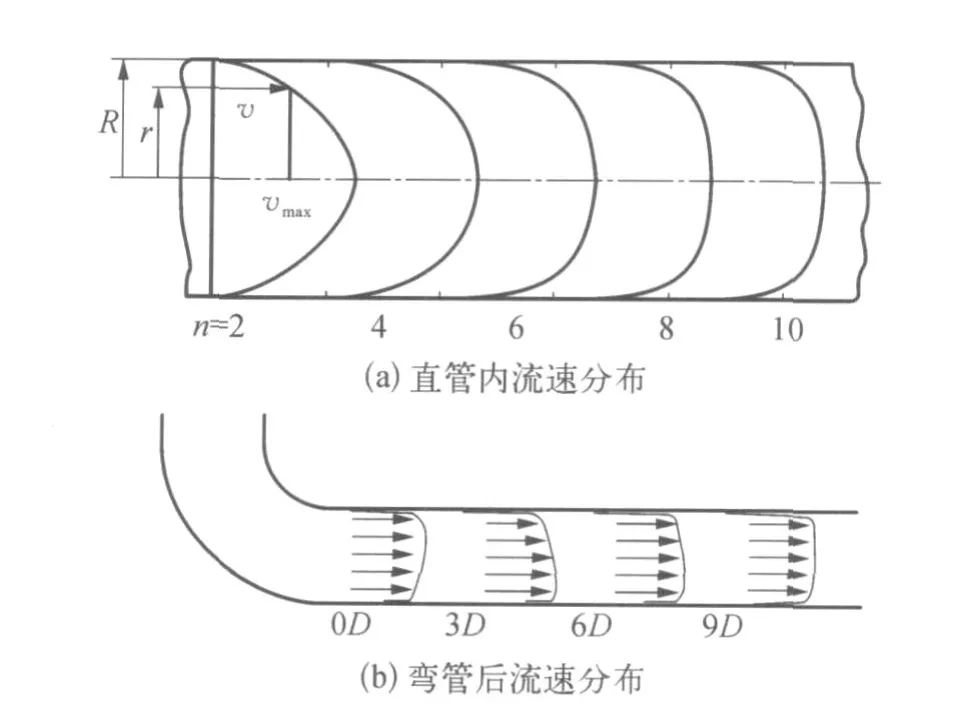
图1 流速分布图

该模型所描述的流速分布在管壁附近 (r= R)和管道中心 (r=0～ 0.2R)两处,无论雷诺数为多少,均与实际情况有较大偏离。因此,用该模型来拟合实际管道中的流速分布吻合度不够高。

从边界层的半经验理论出发,考察圆管中充分发展的湍流问题。整个边界层可分为粘性底层、缓冲层和湍流核心层三部分[5],以下三位学者分别提出了按边界层分段的速度分布公式:

a)Von Karman表达式:

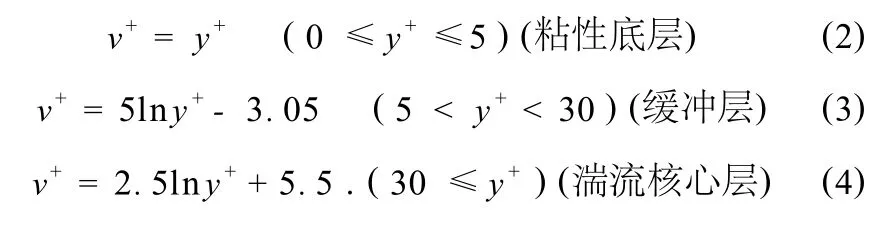
b)Taylor表达式:

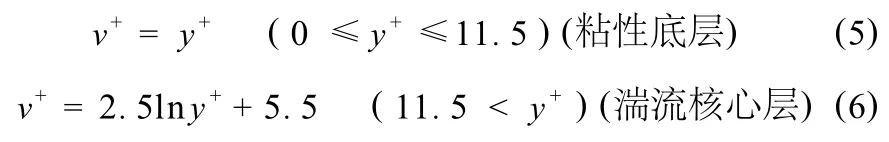
c)Spalding表达式[6]:

式中 v+——无因次流速;y+——无因次距离;常数B=5.2,K=0.41。

这些经典的分段式模型与实验数据吻合得较好,但必须考虑自变量范围分段计算的过程,增加了实际工程计量的难度。为解决这一问题,国内有学者于20世纪80年代对Spalding式进行了改进,得到了统一描述整个管道截面上的速度分布模型如下[7-8]:

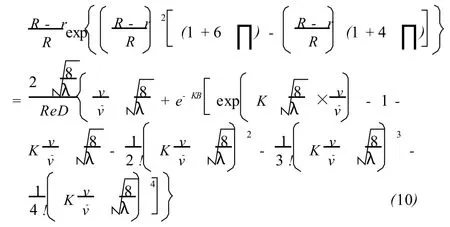
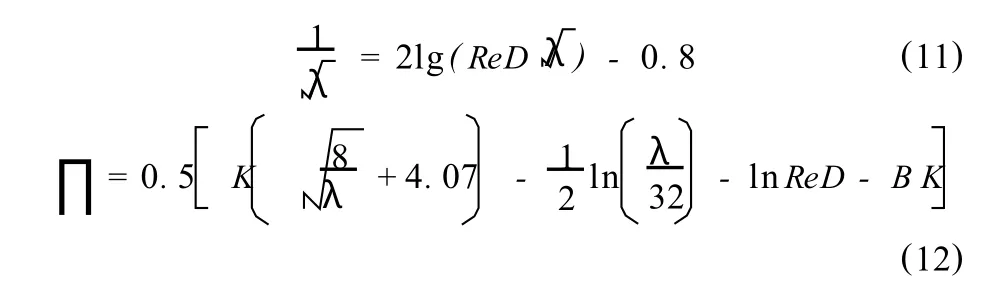
把式(11)和(12)代入式(10),可得到在不同ReD下之间的关系,它就是以ReD为参量的的一族曲线,当预先给定一ReD值时,可借助计算机而得到不同下的值。

文献[13]中通过对比光滑圆管中指数公式(1)和统一分布式(10)的解,证明了统一分布式与实际情况更吻合。

在图1中,选择一个具有稳定流速分布的面,在该面上选择多条直径上的测点,用皮托管进行流速测量,当测得足够多的点后,可获得该面的速度分布曲线。

然而,由于工业现场各阻力件,管道粗糙度以及前直管段长度不足等因素对流动的影响,管道截面的流速分布可能有畸变,不再是对称的。因此,必须有针对性地对需要获得流量值的管道的某一截面进行流速分布测量,获得流速分布方程,再根据该流速方程以及管道中某点的坐标推算出流速。

2 实验数据与结果讨论

实验在300 mm管道气体流量装置上进行,实验装置框架如图2所示,整套装置长50D,实验段前后各有20 Hz的直管段长度。此套装置采用吸气式,动力源为变频器(6～50 Hz)控制的风机,正常工作时管内流速范围为1.30～11.74 m/s。标准表采用精确度为±1%的TBQ系列气体涡轮流量计,流量范围为320～6 500 m3/h,工作温度为-30～60℃,大气压力为86～106 kPa,相对湿度为5%～95%RH。

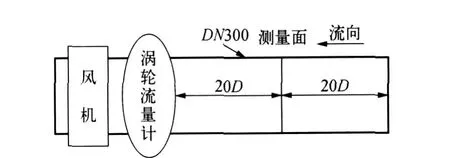
图2 实验装置框架

由于变频器的频率在30 Hz以上时,管道受风机扰动,产生一定振动,影响测量精确度,实验中选用10 Hz的频率,实验温度为20℃,使用皮托管测量,皮托管半径为2 mm。实验中,通过调节变频器频率,测量管道内不同流速下,在图2所示的测量面上的流速分布。10 Hz频率下测量面的流速分布图,实验数据如图3所示,从图3中可以看出,该面上是充分发展的湍流速度分布。分别取直径上坐标为-140,-100,-50,0,50, 100,140七个点,利用式(1)和式(10)计算点流速,如图4所示。

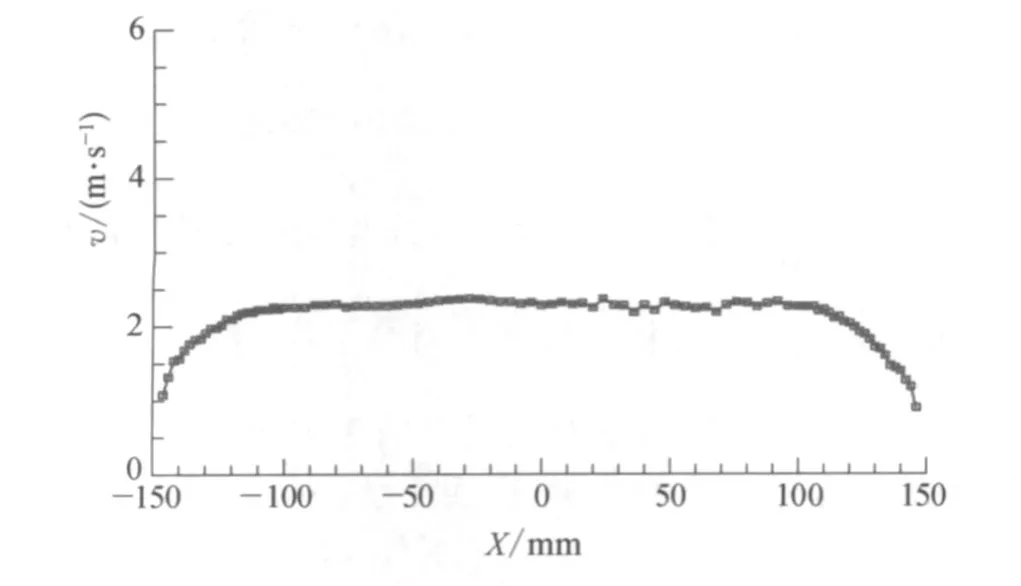
图3 测量面上的流速分布曲线

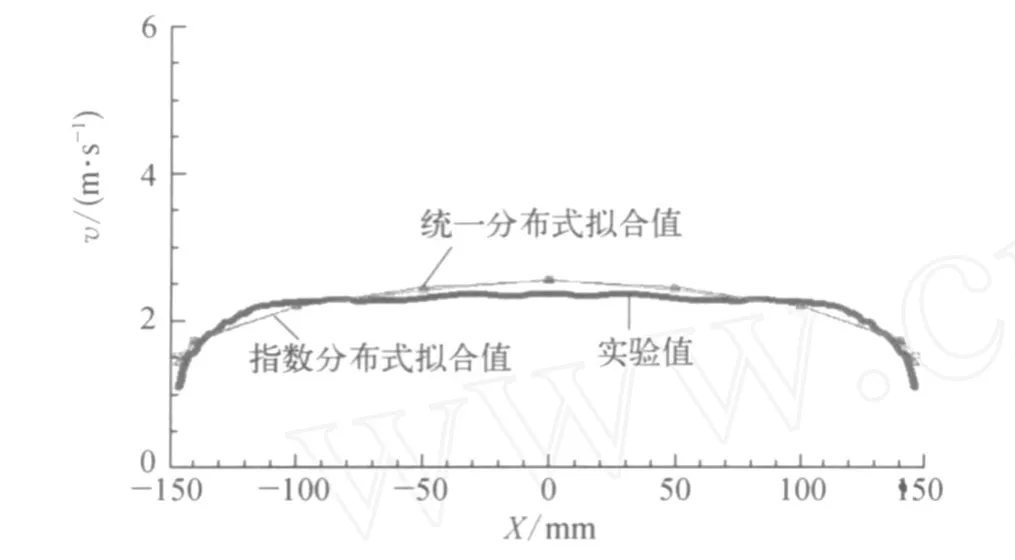
图4 实验值与拟合值的对比曲线

为准确计量平均速度,如图5所示,在测量面的一条直径上均匀地取10个点,r值分别为±15 mm, ±45 mm,±75 mm,±105 mm和±135 mm。采用速度面积法获得该面的流量值,与式(1)和式(10)的流量对比,并与涡轮流量计测得的数值进行比较,由于涡轮流量计的示值的最后一位会发生上下跳动,取一定时间内的平均值,见表1所列。

表1 各种方法的流量值对比 m3/h

通过计算发现,通过公式拟合的流速与实际流速在大部分区域基本吻合,且统一分布式(10)较式(1)在管中心部分更接近实际值。

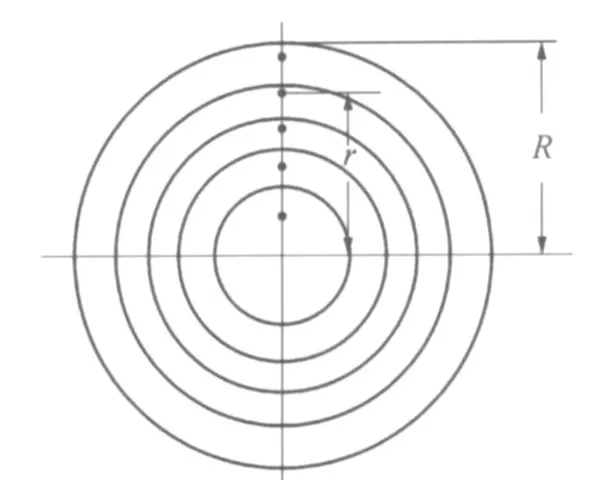
图5 圆管速度面积法测点位置

3 结束语

该文通过测量圆管内的某个面上的流速分布,获得流速分布曲线后,用指数分布方程和统一分布式方程拟合该曲线,发现拟合曲线上的点流速与实际流速较接近。通过这种方法,可以在之后的流速测量中直接利用该面的流速分布曲线及统一分布式方程推算各点的流速值。

该方法必须对不同的管道分别测取某个面的流速分布,获得对应的流速分布曲线,然后用统一分布式方程进行拟合,并对方程做必要的修正。最后达到通过方程和流速分布曲线直接推算流速的目的。

[1] 毛新业,李伟健.大管道气体流量检测仪表[J].电力设备, 2008,9(12):8-11.

[2] 张东飞,苏中地,史晓妍,等.不同雷诺数下均速管流量计流量系数的确定[J].中国计量学院学报,2007,18(1): 18-21.

[3] 毛新业.大管道气体流量检测仪表[J].传感器与仪器仪表, 2006,10(10):56-58.

[4] 孔 珑.工程流体力学[M].北京:中国电力出版社,2007: 106-107.

[5] 苏中地.非牛顿幂律流体圆管湍流的新速度分布式[J].中国计量学院学报,1997,(1):111-115.

[6] SPALDING D B.A Single Formula for the Law of the Wall [J].Journal of Applied Mechanics,1961.

[7] 张维一,龚家彪.圆管中充分发展湍流的速度分布与平均流速位置的研究[J].计量学报.1983,4(1):1-5.

[8] 薛恨春,龚家彪.充分发展圆管流速分布统一模型及其平均流速位置的研究[J].计量学报,1985,6(4):274-278.

[9] 张东飞,苏中地,何馨雨.一种适用于均速管测量的管内统一速度分布式[J].中国计量学院学报,2007,3: 200-203.