基于Agent的电子商务在线议价研究

江资斌,王春玲

(湖南大学工商管理学院,湖南长沙 410082)

基于Agent的电子商务在线议价研究

江资斌,王春玲

(湖南大学工商管理学院,湖南长沙 410082)

针对电子商务中交易双方的议价问题,引入Agent,建立了通用的基于多Agent的在线议价模型。通过构造Agent报价策略的概率密度函数,并考虑议价双方的下一步期望价格和保留价格,构建了基于价格的议价算法,该算法考虑了Agent的偏好、议价时间约束等参数,而且该议价算法能动态地修改可能的报价区间范围,并具有一定的学习能力,使议价过程能够较好地反映交易双方的心智态度,可模拟传统交易中的议价过程。

电子商务;Agent;议价模型

一、引 言

随着网络技术和计算机软件技术的飞速发展,电子商务伴随着一种全新的购买方式越来越多地走进了人们的生活,社会生活的各个领域都受到了深远的影响。人们期待电子商务在降低交易成本的同时,能和传统商务一样,通过议价的方式来满足交易双方的各种偏好,以期获得较好的供货、优惠的价格和高质量的产品。

一些研究者分别从基于博弈论、启发式方法、智能优化算法和基于论据理论的角度针对该问题展开了研究[1-4]。然而,基本的博弈论模型一般只适合于对结果的分析,对于电子商务中的在线议价问题,其结果通常是未知的,应更加关注对其过程的分析。启发式方法由于基于过多的假设,需要反复模拟才能得到较理想的结果。而对论据的研究,对于论据的产生和选择,论据可信度的判断,仍然缺少具有更高实用性的推理模型。面对激烈的市场竞争,如何优化网上交易的议价过程和提高效率,并使参与者双方都满意其结果,以实现双赢,这些问题亟需解决。

起源于分布式人工智能(DAI)研究领域的多Agent系统(MAS)具有自主性、分布性、动态性、协调性等特点,并能通过多智能体协商进行分布式问题合作求解(DPS),正好与其需求相吻合。在电子商务中,议价是一种不完全信息下的多阶段连续过程。基于Agent的方法需要考虑一个很重要的问题,即在考虑对方报价、自身环境特点和信念的基础上如何确定下一步报价策略。Zeng等人基于贝叶斯决策提出了一个具有学习能力的Bazaar模型,Bazaar模型是一个静态模型,它没有具体的实现过程,且没有考虑协商过程的约束条件和协商策略等因素[5]。高璐等人研究了企业基于Agent的自动协商,设计了一个包含时间策略、资源策略和模仿策略的多策略模型[6]。叶斌等人从统计的角度分析了多Agent协商行为的行为效用,从而为更好地设计多Agent系统的组织规则和协商策略提供了效用依据[7]。然而这些模型和方法一般处于理论研究阶段,不容易实现,且交易双方各自追求自身利益最大化,没有考虑“双赢”,要使它们能适用于电子商务的自动议价,还需进一步扩展。为此,本文提出了一种基于Agent的电子商务议价模型,并设计了相应的报价策略和议价算法,算法考虑了Agent双方策略的采用,以及时间约束,使得议价效率提高,并能提高交易双方的效益,实现双赢。

二、在线议价模型

在实际的议价过程中,交易的双方都希望自己的效用最大化,都希望通过不断的报价和反报价来达到自己的目的。考虑到交易的时间、报价和反报价、效用评价等因素,交易双方的Agent将采用不同的策略。为此,本文构建了如下议价模型:

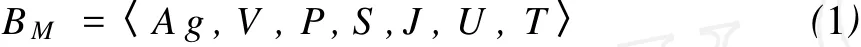
第一,Ag为参与议价的Agent集合。设卖方Agent为 S集,B为买方Agent集,则 Ag=S∪B。

第二,V={v1,v2,…,vn}为议价议题集合。在电子商务的在线交易中,指某产品或服务的价格、交货期限、质量等因子。

第三,P为议价协议的集合。如同时报价和轮流报价等议价协议。

第四,S为议价策略的集合,包括单一让步策略、组合让步策略和遗传算法搜索策略等。

第五,J为议价中Agent的联合行动集合,包括接受 (Accept)、拒绝 (Refuse)、报价 (Offer-Proposal)与反报价(Reject-Proposal)等。

第六,U={US,UB}为Agent的效用评价集合。

以上是电子商务中基于多Agent的在线议价模型,模型主要包括参与在线议价的Agent集合、议价议题、议价交互协议和议价策略等。

三、议价算法

(一)议价过程描述及假设

假设议价参与者为 Ag={s,b},其中s表示卖方Agent,b表示买方Agent,该产品的单件价格s和b查询各自的知识库,估计其处于[l,h]之间。设RPb为b的保留价格,即b所能接受的该产品单件最高价格;设 RPs为s的保留价格,即所能接受的该产品单件最低价格。假定双方都不知道对方的保留价格。此时,议价的成交价格应处于区间[RPs,RPb],如图1所示。

交易双方都有自己的报价信念,假定在一次报价过程中,其信念固定。在一轮交互之后,买卖主体可能会根据情况改变其出价信念。在现实生活中,买方通常希望以最低价格获得某一商品,通常买方效用函数为单调递减的,即如果v1b≤v2b,那么Ub(vs,v1b)≥Ub(vs,v2b)。卖方效用函数正好相反,单调递增。假设议价成本主要为通信费用,可以忽略不计,如果议价失败,双方的效用为0。

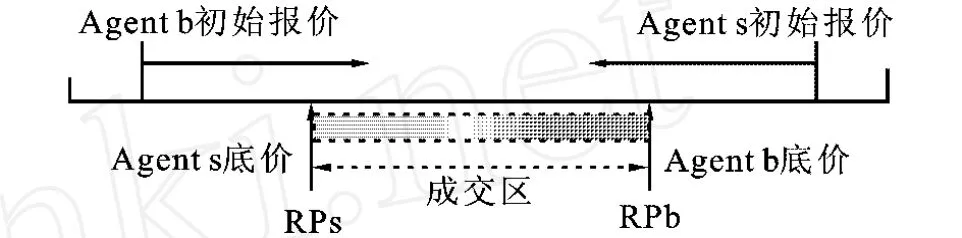
图1 议价的成交价格区间图

买方 b效用函数可定义为:

若以实现双赢为目标,就必须同时实现买卖Agent效用的最大化,为此定义联合效用函数 UJ为:

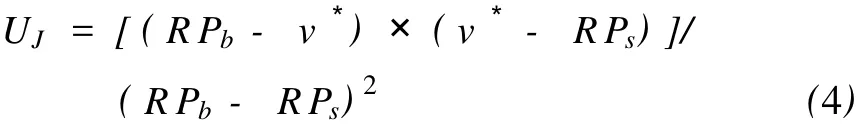
其中 v3为成交价格,由此函数可知,当 v3为 RPs和RPb的数学平均值时,UJ达到最大值0.25。

(二)报价策略及参数分析

显然,Agent采用何种报价策略,以使自己在获得尽可能多收益的同时又能为对方接受,这是议价成功的关键。然而,要求所有Agent采用某一固定策略模型是不现实的,Agent需要在议价过程中不断调整自己的报价策略,以期获得更多的收益,因此,对策和学习是Agent参与在线议价的重要机制。

在式(8)中s的报价策略若采用式(5),则为保守策略,若采用式(6)则为激进策略,与 b的情况正好相反。在议价过程中,若不考虑买方的报价则

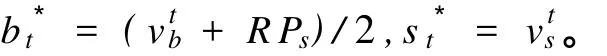
假定双方约定最大协商次数已知,以买方 b的报价概率密度函数为例,t越大,即离议价结束期限越近,报价概率分布曲线越陡峭。这表明当b采用信念更新方法如式(5)时,其报价靠近,这时随着议价剩余的时间越来越短,b相信s不大可能改变其报价,因而其报价作出较大的让步。当 b采用式(6)更新信念时,其报价靠近,这时 b相信s报价不合理,随着议价剩余的时间越来越短,b相信s有可能作更大的让步,因此 b让步较小。

参数β用于调整协商时的让步程度,β越大,概率密度曲线越平缓,对于式(5),b的报价偏离越远些,因而b让步较小;对于式(6),b的报价偏较远。当β足够大,式(5)和式(6)收敛于均匀分布报价。

(三)议价算法步骤

基于以上讨论的报价策略,本文设计了买卖双方Agent的议价算法,具体步骤如下:

步骤 1:针对某产品,买方 Agent b向卖方Agent s发出议价请求,置 t=1,=l,=h,并生成初始报价,s亦生成初始报价,b和s通过通讯语言约定 tmax。

步骤3:b采用式(5)或式(6)更新其信念,并根据式(7)生成反报价。

步骤4:采用式(5)或式(6)更新其信念,并根据式(8)生成反报价,转步骤2。

步骤5:b和s签订协议,议价结束。

步骤6:议价失败。

四、数值算例

在B2B电子商务交易平台,假定某产品的市场价格范围为[50,100],买方考虑其议价成本,认为最多讨价次数为 tmax=10,其私有信息保留价格为RPb=90,则它可以接受的价格范围为[50,90],报价策略分别采用式(5)和式(6)。假定第一次期望报价=55,由此确定买方报价策略特征参数βb,为简化计算,并假定以后的交易中βb值保持不变。

对于s,其保留价格为 RPs=60,因而它可以接受的价格范围为[60,100],报价策略分别采用式(5)和式(6);假定第一次报价=94,由此确定它的报价策略特征参数βs,同样为简化计算,假定以后交易中βs值保持不变。

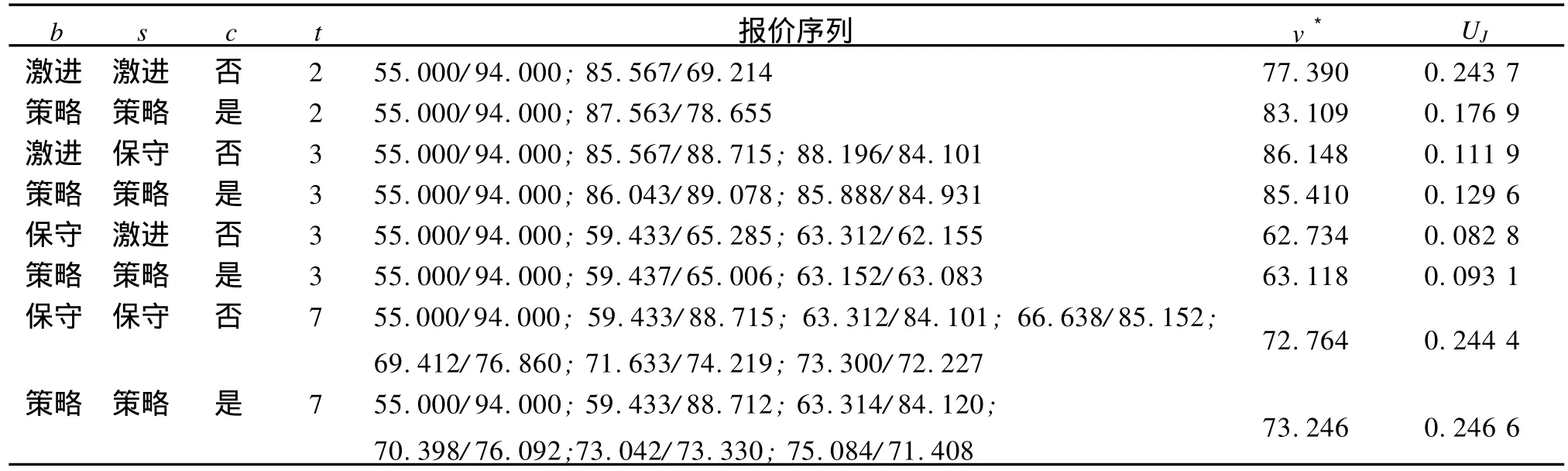
由于买方 b和卖方s分别可以采取式(5)和式(6)的报价策略,报价又可基于不考虑对方报价和考虑对方报价,因此总共有8种情况,其计算结果如表1所示。其中 c列表示是否考虑对方报价,t列表示最终协商的次数。对比以上各种不同组合的情况可知,当某一方 采用激进报价策略时,它一般会在价格方面吃亏。这是显而易见的,因为它每次让步幅度比较大。

表1 考虑对方报价与否的议价过程比较表

b s c t 报价序列 v3 UJ激进 激进 否 2 55.000/94. 000;85.567/69.214 77.390 0.243 7策略 策略 是 2 55.000/94. 000;87.563/78.655 83.109 0.176 9激进 保守 否 3 55.000/94. 000;85.567/88. 715;88.196/84.101 86.148 0.111 9策略 策略 是 3 55.000/94. 000;86.043/89. 078;85.888/84.931 85.410 0.129 6保守 激进 否 3 55.000/94. 000;59.433/65. 285;63.312/62.155 62.734 0.082 8策略 策略 是 3 55.000/94. 000;59.437/65. 006;63.152/63.083 63.118 0.093 1保守 保守 否 7 55.000/94. 000;59.433/88. 715;63.312/84. 101;66.638/85. 152;69.412/76. 860;71.633/74. 219;73.300/72.227 72.764 0.244 4策略 策略 是 7 55.000/94. 000;59.433/88. 712;63.314/84. 120;70.398/76. 092;73.042/73. 330;75.084/71.408 73.246 0.246 6

对于买方来说,当卖方上一次报价高于自己心中的最高保留价格而不能成交时,该算法可使买方加快抬高价格的幅度。然而当卖方上一次报价低于自己心目中的最高保留价格时,买方觉得成交有望,故而会减缓自己的报价幅度。

卖方正好相反,当买方上一次报价小于自己心中的最低保留价格时,该算法可使卖方加快降低自己价格的幅度。然而当买方上一次报价高于自己心目中的最低保留价格时,卖方觉得成交有望,故而会减缓自己报价的幅度。

在算例中,因为买方先报价,对卖方报价进行学习。然而买方的第一次报价55往往低于卖方的保留价格60,为了能够协商成功,买方往往会加快自己的提价幅度,故而最后的议价结果往往比没有进行学习的成交价格要高一些,卖方则相反。这样,买方相对吃亏,以高价买回了产品。

另外,可以看出考虑对方报价比不考虑对方报价策略,联合效用普遍要高,这有利于实现双赢目的。这些都和现实生活中的议价实际心理状态相似。因此,算法能较好地模拟现实生活中的议价过程,在B2B和B2C电子商务中均具有较强的实用性。

五、结束语

本文通过研究基于Agent的方法,来解决电子商务中的议价问题。针对Agent的议价问题,设计了通用的议价模型,并为Agent设计了不同的报价概率密度函数,Agent通过采用这些指数分布概率密度函数,可更新对方的信息,实现议价过程的自学习,提高交易效率。同时应该注意到本文的议价算法只考虑了交易双方的价格因素,在电子商务中可能还要考虑其他诸多因素,如交货时间、产品质量等[8]。另外,买方可能要同时和几个卖主就某一产品进行议价,这都使得问题会变得更加复杂。以上诸种情形还有待于进一步研究。

[1]道格拉斯·盖尔.一般均衡的策略基础——动态匹配与讨价还价博弈[M].上海:上海人民出版社,2004:53-71.

[2]黄京华,马晖,赵纯均.面向电子商务的基本遗传算法的Agent谈判模型[J].管理科学学报,2002,5(6):17-23.

[3]Li Jian,Wang Cong,Yang Yi-xian.An adaptive genetic algorithm and its application in bilateralmulti-issue negotiation[J].The Journal of China University of Posts and Telecommunications,2008,15(1):94-97.

[4]Parsons S,Sierra C,Jennings N R.Agents that reason and negotiate by arguing[J].Journalof Logic and Computation,1998,8(3):261-292.

[5]Zeng D,Sycara K.Benefits of learning in negotiation[J].International Journal of Human Computer Systems,1998,48(1):125-141.

[6]高璐,毛波.基于MAS的企业供应链模型中谈判过程的研究[J].系统工程理论方法应用,2002,4(11):304-309.

[7]叶斌,马忠贵,曾广平,等.多Agent协商行为的效用分析[J].控制与决策,2004,19(12):1332-1336.

[8]Lai GM,Sycara K A.Generic framework for automated multi-attribute negotiation[J].Group Decision and Negotiation,2009,18(2):169-187.

Agent Based Online Bargain ing in Electronic Commerce

JIANG Zi-bin,WANG Chun-lin
(Schoolof Business Administration,Hunan University,Changsha 410082,China)

M ulti-agent was introduced to study the issue of bargaining in Electronic Commerce(EC),and a generic model formulti-agent bargaining in ECwaspresented firstly.Then,constructed p robabilities function as bid tacticsof agents and taken the expected price of both sides in the next turns and their reserved price into account,a price based bargaining algorithm was proposed.The algorithm considered the p reference of agents and the restriction of time etc.By employing thisalgorithm,agent canmodify itsbid zone dynamically and learn about the opponent’s bid price.In thisway,the algorithm can reflect the attitudeof the two transaction parties and simulate the iteration of offering price very well in reality,w hich may p romote the efficiency of bargaining and attain better result.

electronic commerce;Agent;bargaining model

(责任编辑:李 勤)

F062.5

A

1007-3116(2010)04-0109-04

2009-11-26

湖南省2008年SIT计划重点项目《基于Agent技术的电子商务在线议价研究》;国家自然科学基金项目《实现多级供货能力承诺的虚拟企业生产计划协同优化研究》(70572060)

江资斌(1976-),男,湖南浏阳人,管理学博士,讲师,研究方向:电子商务与智能管理信息系统。

【统计应用研究】