基于FPGA的并行扫频DDS的实现

张卫清，谭剑美，陈 菡

华东电子工程研究所，安徽合肥 230031

基于FPGA的并行扫频DDS的实现

张卫清，谭剑美，陈 菡

华东电子工程研究所，安徽合肥 230031

本文介绍了直接数字合成技术(DDS)的工作原理，深入分析了结构组成，在传统串行DDS结构的基础上，提出了一种具有扫频功能的并行DDS结构，同时对居于CORDIC算法的相幅变换方法进行了详细叙述，最后对提出的并行DDS结构进行了理论仿真和硬件实现，证明了该结构在不提高DDS工作时钟的情况下可获得较高的输出信号。

直接数字频率合成器；CORDIC；并行DDS

1 概述

直接数字合成技术(Direct Digital Synthesis，DDS)是由美国学者J.Tierney等在1971年提出的，它是一种全数字频率合成技术，是一种新型的频率、相位波形合成技术。它充分利用了目前大规模集成电路的快速、低功耗、大容量、体积小等特点。与传统的频率合成器相比，具有相位噪声低、频率分辨率高、转换迅速等优点，它的频率、相位变化连续性可以用于相位及频率调制，快速频率变换特性可用于频率捷变和扩频系统[1，2]。因此，DDS可广泛地应用于雷达、电子对抗、移动通信等领域。随着大规模集成电路在工艺和材料上的不断创新和近年来对其算法的不断改进，DDS越来越因其明显的优势而倍受瞩目。

2 DDS的组成及其工作原理

一个具备扫频功能的DDS典型结构如图1所示，其主要由频率累加器、相位累加器、相-幅转换器、DAC及相应的滤波器（低通或带通）组成。DDS的工作原理为：对于一个给定的系统工作时钟fC相位累加器在每一个时钟上升沿与频率控制字(K)累加一次，当累加器完成2N(N为累加器的长度)次运算后，相位累加器相当于做了一次模余运算。正弦查找表在每一个时钟周期内，根据送给ROM的地址取出存储在ROM表中与该地址对应的正弦幅值，最后将该值送给DAC与LPF实现量化幅值到一个纯净的正弦信号间的转换，同时正弦信号的相位及幅度可以根据需要分别进行控制。相位累加器的作用是根据从步进寄存器输入的频率控制字，以系统时钟频率fC为采样率，在2π周期内对相位进行采样。如果步长为K，采样点数为

从而改变频率控制字K就可以精确地改变频率，从式(1)可知，可变的最小频率间隔，即最小频率分辨率Δfmin为：

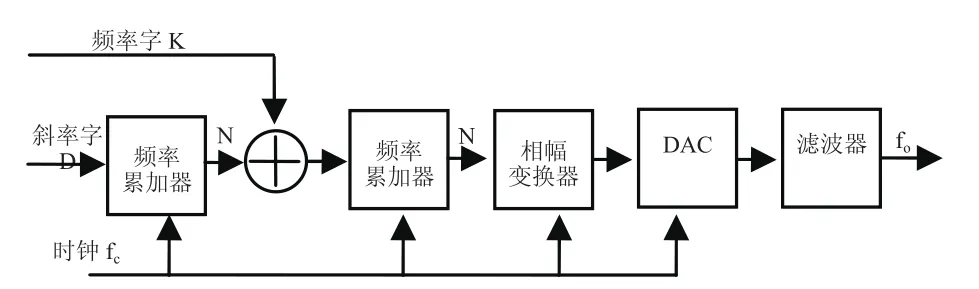
图1 扫频DDS原理框图

3 DDS并行结构实现

3.1 DDS并行结构的推导

由DDS的原理我们知道，DDS输出最高频率为fC/2，因此要想获得较高的输出频率，必须提高DDS系统工作时钟fC，然而通常情况下受器件限制，fC不可能很高，尤其是在用FPGA实现DDS的情况下，因此有必要寻求另一种方法，在不显著提高fC的情况下，获得较高频率的输出信号。

让我们再次回顾图1所示的扫频DDS结构，在系统时钟fC的作用下，fC每触发一次，相位累加器输出一个N bit的相位值，我们不妨列出起始时刻相位累加器的输出状态：

上式X(0)～X(11)为相位累加器从起始时刻开始连续12个状态的输出，我们可以把相位累加器输出的值分为两部分，一部分只与频率字有关（记为Xk），另一部分只与斜率字有关（记为Xd），因此可以得出以下规律，

其中4n*K为加法器前一个时钟输出的状态，K为输入的频率字，因此Xk(4n)，Xk(4n+1)，Xk(4n+2)，Xk(4n+3)四个连续的状态就被4n*K和K两个状态表示出来，因此Xk的累加过程可以用图2所示的结构来表示

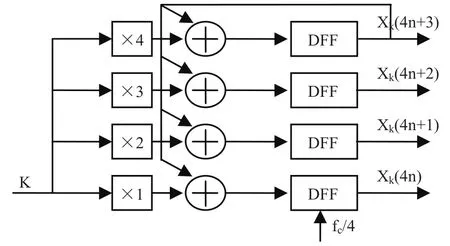
图2 频率字并行累加结构框图

同理，对于Xd(n)可以进一步推导出以下公式：

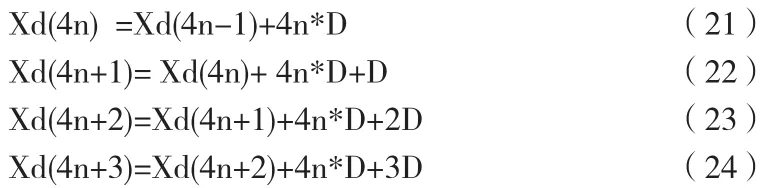
其中Xd(4n-1)+4n*D为加法器前一个时钟输出的状态，D为输入的扫频斜率字，因此Xd(4n)，Xd(4n+1)，Xd(4n+2)，Xd(4n+3)四个连续的状态就被4n*D和D两个状态表示出来，因此Xd可以用图3所示的结构来表示

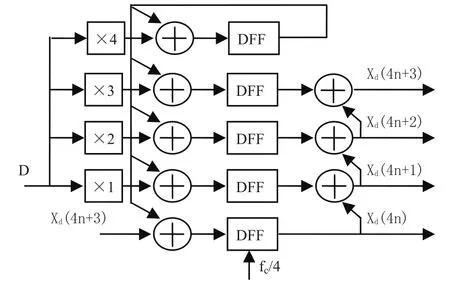
图3 斜率字并行累加结构框图

因此，如图1所示的DDS结构中的频率累加器和相位累加器可由图2和图3两结合的结构组成，新的并行DDS结构如图4所示。

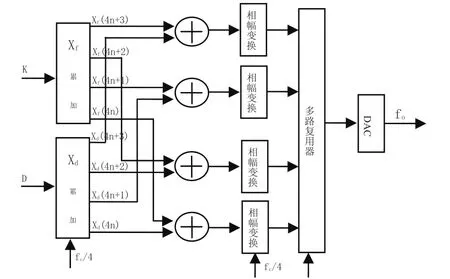
图4 扫频并行DDS结构框图

我们可以看到这种结构的优点是把相位累加器和频率累加器的内部工作时钟降低为fC/4，反过来也就是提高了4倍的时钟频率，在每输入一个频率字和斜率字的状态下，4个加法器同时输出4个连续的状态，经过多路复用器进行选通，保证了在外部每个fC的情况下都可以输出一个值，这样大幅度降低了流水线累加器在高速时钟信号下工作所产生的功耗，并且提高了整个系统时钟工作的频率，提高了DDS的输出频率。

3.2 相幅转换的实现

相位-幅度转换方法主要有查找表，多项式展开法以及Cordic算法，查表法通过事先计算好正弦或余弦值，将其存储在只读存储器中，然后将相位累加器输出的相位作为地址从ROMA中通过查表获取正弦或余弦值，其缺点是ROM要专用大量的片内资源，Sunderland提出的粗、细ROM结构[4]及其修改形式，其最高压缩比为59:1，文献[5]提出的Nicholas结构算法是一种基于数字化优化的方法，可以根据实际参数优化计算出粗、细ROM的容量及数据位数，其压缩比可以达到128:1。多项式展开法是利用泰勒级数展开来实现相位幅度的转换，取Taylor级数前三项分别赋予不同的权值后存于3个ROM，最后由运算电路合成，这种方法可以得到64:1的压缩比，但要获得较高的精度，需要使用较高的阶数，电路实现比较复杂。CORDIC算法则是一种纯算术的三角函数计算方法，它能通过简单移位、加法等多次迭代给出精确结果，比较适合位数大于14位的DDS，同时也特别适合FPGA实现。CORDIC，又名坐标旋转数字计算，是J. Voider等人于1959年在设计美国航空导航控制系统的过程中提出来的一种算法[78]。下面就简要地介绍一下CORDIC算法的基本数学思想。

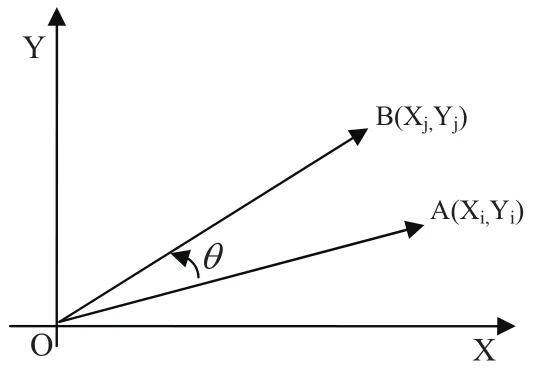
图5 向量旋转坐标图

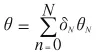
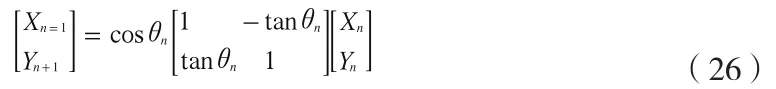
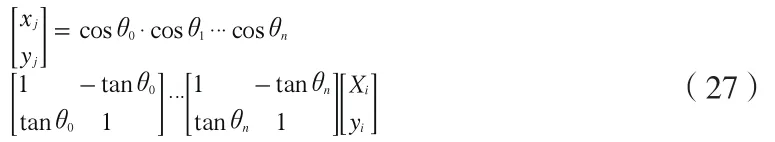
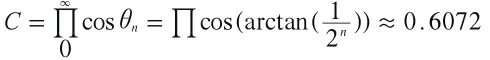
不考虑常量C，那么式(26)可以简化为

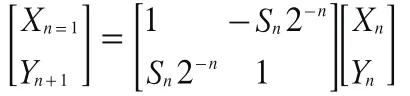
上式Sn=｛-1,1｝，再次回到图5，我们假定：

起始向量OA为[Xi,Yi,θi]=[1,0,0]

终止向量 OB 为[Xj,Yj,θj]=[cosθ,sinθ,θ]

经过一系列特定角度θn的依次旋转，由矢量OA旋转到矢量OB即可得到cosθ，可见，CORDIC算法是通过将一个初始位置与X轴重合、方向与X轴一致、起点为原点、终点在单位圆上的向量绕原点作一系列特定角度的顺时针或逆时针旋转叠加来渐进逼近输入角度，从而计算出输入角余弦值。

4 仿真及硬件实现

为了验证本文推导的具有扫频功能的并行DDS结构的正确性，先利用matlab对算法进行了仿真，同时用硬件描述语言Verilog对算法进行了实现，最后导入ModemSim对该结构进行了仿真，仿真参数设置信号中心频率223MHz，带宽2.5MHz，时宽40us，DDS工作时钟(fc)为600MHz，仿真结果如下：

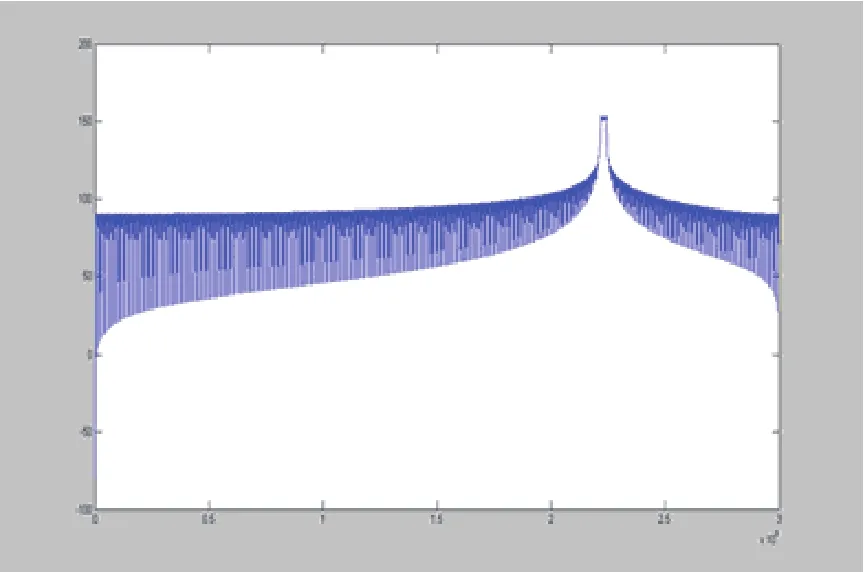
图6 线性调频仿真结果图

采用FPGA+DAC硬件平台验证本文推导的并行DDS，FPGA为ALTERA 公司StratixⅡ 系列，型号：EP2SEF1020C4；DAC为ADI公司14位转换率1.2GHz的器件，型号：AD9736。FPGA内部各累加器及相幅转换器工作时钟为150MHz，利用FPGA内部高速并串转换模块对四路相幅转换器的输出进复用，实现了利用600MHz工作时钟直接产生中心频率为223MHz，带宽2.5MHz，时宽40us的线性调频信号，测试结果如图7所示。

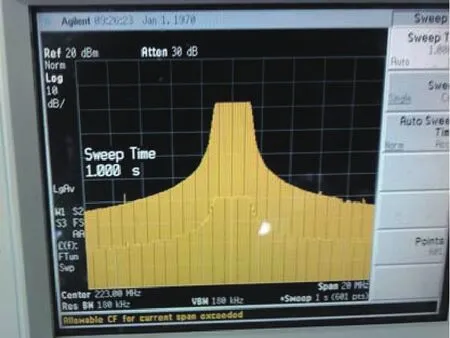
图7 DAC输出频域信号图

5 结论

本文提出了一种新型扫频并行DDS结构，很好地解决了在FPGA内部采用低速时钟产生高频率信号输出的难题，同时利用CORDIC方法实现了相幅转换。本文提出的并行DDS结构非常适合FPGA实现，在直接信号产生和任意波形产生等系统中可以广泛应用。

[1]TierneyJ，Rader C，Gold B.A digital frequency sysnthesizer[J].IEEE Trans Audio Electroacoust，1971，54（19）:48-56.

[2]VankkaJ，Halonen K.Direct digital Synthesizers theory，design and applications[M].NorwellKluwer Academic，2001:337-402.

[3]Tso-Bing Juang，Shen-Fu，Ming-Yu Tsai.Para- CORDIC：Parallel CORDIC Rotation Algorithm.IEEE，2004； 51（8）.

[4]H.T.Nicholas，Ⅲ H.Samueli，B.Kim. The optimization of direct frequency synthesizer performance in the presence of finite word length effects，IEEE Proc 42th AFCS，1988:357-18.

[5]L.J.Kuhner，M.T. A in sworth. A spurious reduction technique for high-speed direct digital synthesizers，IEEE Proc 50th AFCS，1996:920-927

[6]Uwe Meyer-Baese著.数字信号处理的FPGA实现[M].刘凌，胡永生，译.北京：清华大学出版社，2003：55-63.

[7]耿丹.CORDIC算法研究与实现[J].遥测遥控，2007，28 （11）：40.

[8]姚亚峰，付东兵.基于CORDIC改进算法的高速DDS电路设计 [J].华中科技大学学报，2009，37（2）:26-27.

The Implementation of Parallel Sweep DDS Based on FPGA

ZHANG Weiqing，TAN Jianmei，CHEN Han
East China Research of Electronic Engineering

direct digital synthesizer; digital array module; Digital Array Radar

TN941.3

A

1674-6708（2010）22-0203-03

AbsractIn this paper we firstly introduce the concept，architecture of the Direct Digital Synthesizer. Then Base on traditional serial DDS，a parallel architecture DDS wich frequency sweep function was bring forward ，Finally the theory simulation and hardware implementation was given for the parallel structure of DDS，higher output signal can be obtained base on this parallel DDS architecture in condition of lower DDS system clock。