中国大陆地震活动时空分布多重分形特征

陈时军,杜历英,魏绪云

(1.山东省工程地震研究中心,济南 250014;

2.山东省中医药大学附属医院图书馆,济南 200021)

中国大陆地震活动时空分布多重分形特征

陈时军1,杜历英1,魏绪云2

(1.山东省工程地震研究中心,济南 250014;

2.山东省中医药大学附属医院图书馆,济南 200021)

利用多重分形分析方法,考察了中国大陆各构造区地震活动广义应变释放时间和空间分布的多重分形特征。结果表明,中国大陆各构造区地震活动广义应变释放时空分布的多重分形特征差别明显。

中国大陆;地震活动;时空分布;多重分形

0 引言

一定时间、空间范围内地震活动的强度分布为人们了解该时空域内地壳应力变化、研究构造活动特征以及进行地震危险性预测提供了重要信息。因此关于地震活动强度在时空域分布特征的研究一直受到地震工作者的重视。已有的研究结果一致显示地震活动强度在时间域具有非平稳、非线性等特征,在空间域具有非均匀性等特征。地震活动强度分布表现出复杂动力过程所具有的性质。

地震活动强度复杂分布特征可以用多重分形方法进行定量刻画。人们曾利用多重分形方法研究过地震活动事件的时空分布以及地震能量释放等时空分布的多重分形特征[1-7],取得了有意义的结果。本文将在以往研究的基础上进一步分析中国大陆各构造区内地震活动强度时空分布的多重分形特征。

1 理论公式[8]

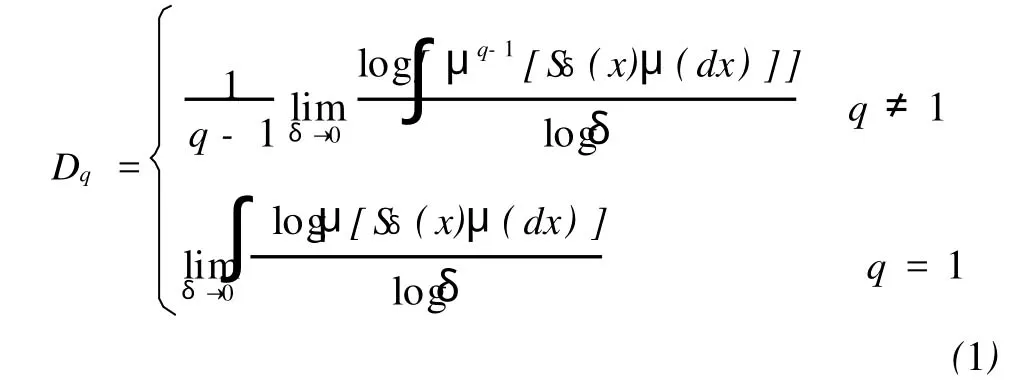
一般而言,多重分形维数谱可用Rényi维Dq定义[7]:其中,Sδ(x)是关于点集 x∈Rd的半径为δ的球体,积分区域为Borel集 Rd上关于概率测度μ的全体。

若将公式(1)的积分域离散为 N个尺度为s的盒子,记第 i个盒子范围内的测度积分为 pi,pi(s)=∫dμ(x),并顾及∫f(μ(x))μ(dx) 为 f 关于测度μ的期望值,则公式(1)可重写为:

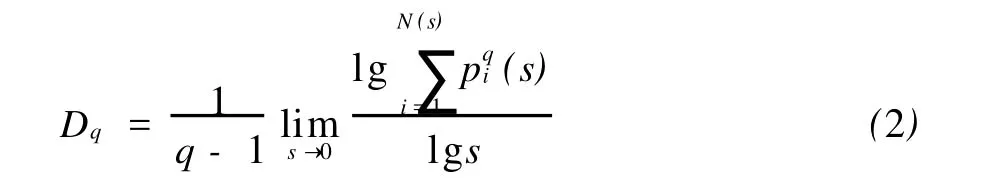
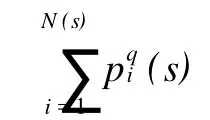
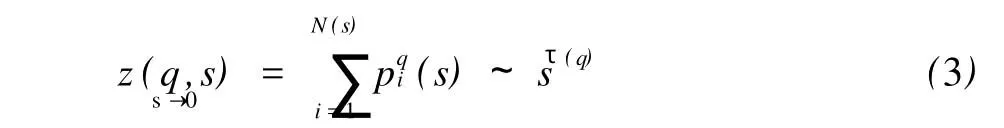
称z为配分函数。覆盖测度μ的盒子数N(s)与盒子尺度s的关系为:

称 f(α)为多重分形奇异谱,它可由τ(q)经Legendre变换

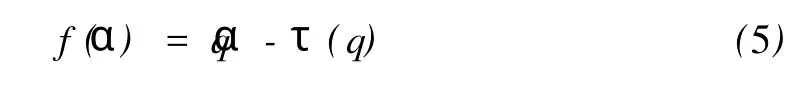
得到。α为 Hölder奇异指数,是 q的函数,可写作α(q),其和τ(q)的关系为:

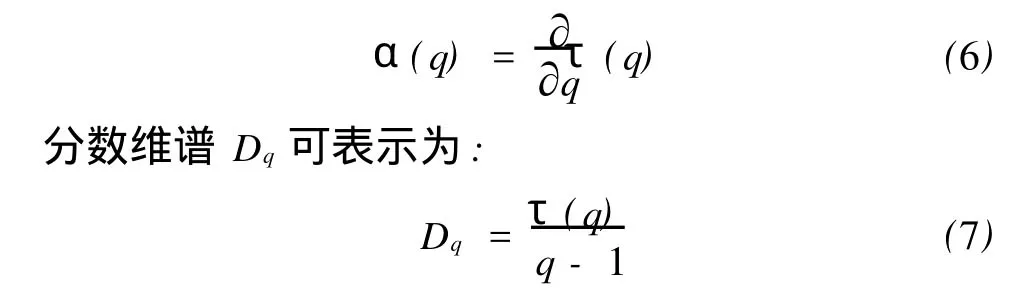
当q=0时,得到盒子维或容量维,D0=f(α(0))=-τ(0);当 q=1时,D1=f(α(1))=α(1)即为信息维。

由于直接计算多重分形谱比较繁杂,需进行Legendre变换,本文采用Chhabra等提出的一种估计多重分形谱的方法[9]。根据该方法,Hölder奇异指数α(q)、多重分形奇异谱 f(α)可写为:

利用公式(8)、(9)、(10)及公式(5)、(7)可计算Hölder奇异指数α(q)、多重分形奇异谱 f(α)以及多重分形维数谱。

2 资料选取与处理

选择SSLib软件包[10]中收录的中国大陆地震目录,研究各构造区地震活动广义应变能释放时间分布的丛集性特征。本文在“板内与板间地区地震活动时空分布多重分形特征研究”[11]的基础上,将中国大陆进一步分为华北构造区、东北构造区、华南构造区、新疆构造区和青藏构造区等几部分,并形成各子地震目录,分析对比各构造区的地震活动多重分形特征。

参照前人研究成果并适当简化,各构造区边界划分后的顶点坐标如表1。为保证所使用目录地震事件记载的完整性,在文献[11]中曾依据震级的平稳性分析和可靠性检验对中国大陆不同地区的“最小完整震级”进行了概略分析,并在分析的基础上选取合适的起始时间与起算震级。同时,为保证地震在时间轴上的密度,资料选取时尽可能取起算震级较低的最新地震目录。各构造区资料选取结果如表2。

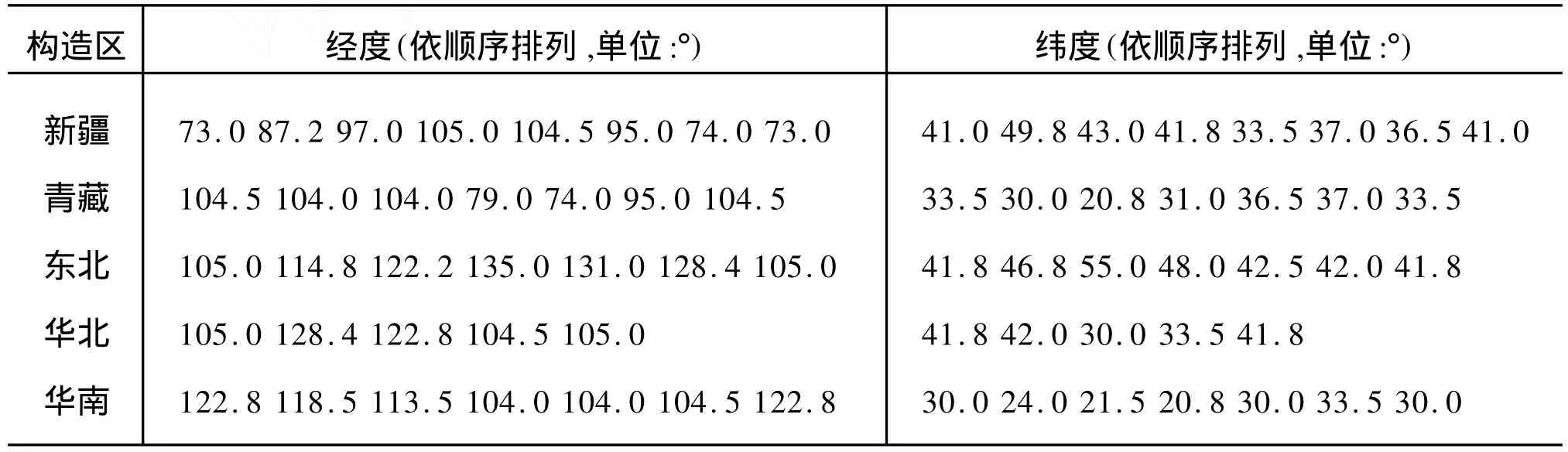
表1 中国大陆各构造区边界经纬度表

表2 中国大陆各构造区资料情况表

此外,为了考察起算震级对多重分形谱估计结果的影响,研究中试算了表2中各地区相应起止时间段内不同起算震级情况下的多重分形谱估计结果,表明各地震目录在给定起止时间和起算震级时可得到稳定的结果。

在研究地震活动强度时间分布丛集性特征时,应将所选定研究区的地震目录依据每时间段至少包含一个大于等于起算震级M0的地震的原则分割为若干等长时段(n≥1),以各时段区间右端时刻为时间标记,利用公式[3-4]:

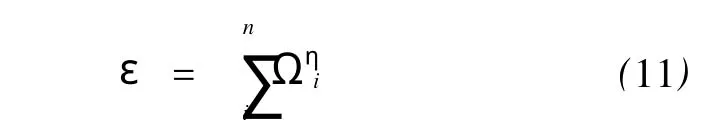
计算各时段区间内的广义应变能释放并形成时间序列。表2中的采样段数就是以这种原则并考虑计算方便而给定的。表2及资料分析表明,仅华南、东北构造区个别段落不满足上述要求,但对结果的影响很弱。

为探索各构造区广义地震应变能释放的丛集特征,研究中η将在区间[0,2]内取多组值。当然,η的取值范围也可以不被此范围所局限,但考虑震级精度、大地震发生率很低以及η取不同值时计算结果的物理意义等,对η的取值范围加以限制是必要的。

3 计算结果与分析

3.1 中国大陆各构造区广义地震应变释放时间分布的多重分形特征

首先将η赋值为 0、2/9、1/3、4/9、1/2、2/3、1.00和1.33,计算各构造区η取不同值时的广义地震应变能序列。表2中由于华南和东北构造区地震时间间隔最大值大于采样时间长度,因此部分采样时段内将可能不包含任何地震。研究中对这种情况人为地将一震级为0.2的虚拟地震赋予该采样时段,以避免计算出现溢出错误。依据计算的广义地震应变释放时间序列,进一步计算得到了τ(q)值随q的变化以及多重分形奇异谱 f(α)随α的变化(为节省篇幅,图1仅给出部分结果)。各构造区部分D0、D1的估计结果列于表3,表4列出了 Hölder奇异指数α的存在范围。

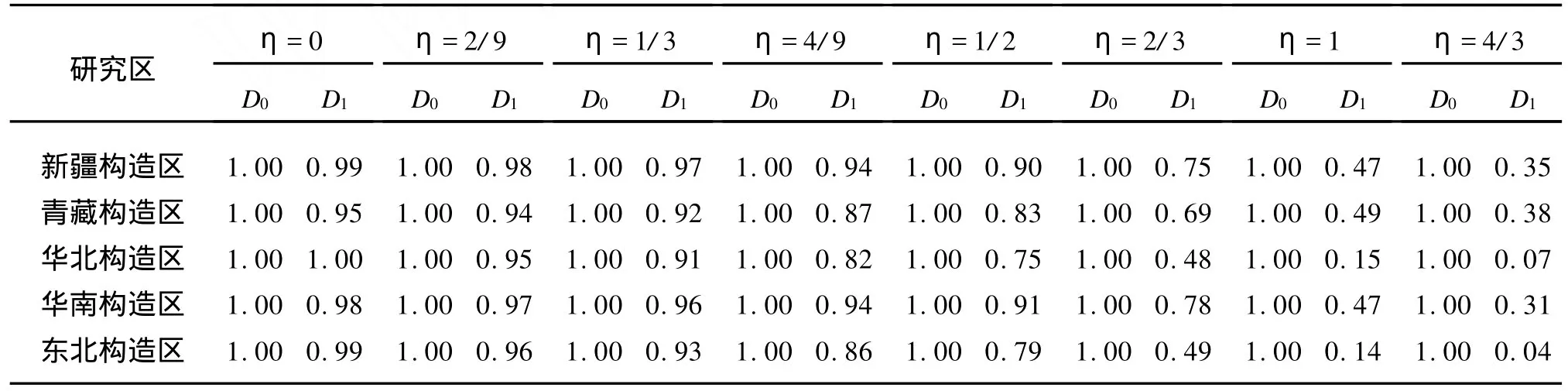
表3 各构造区广义地震应变释放时间分布多重分形谱维数估计结果表

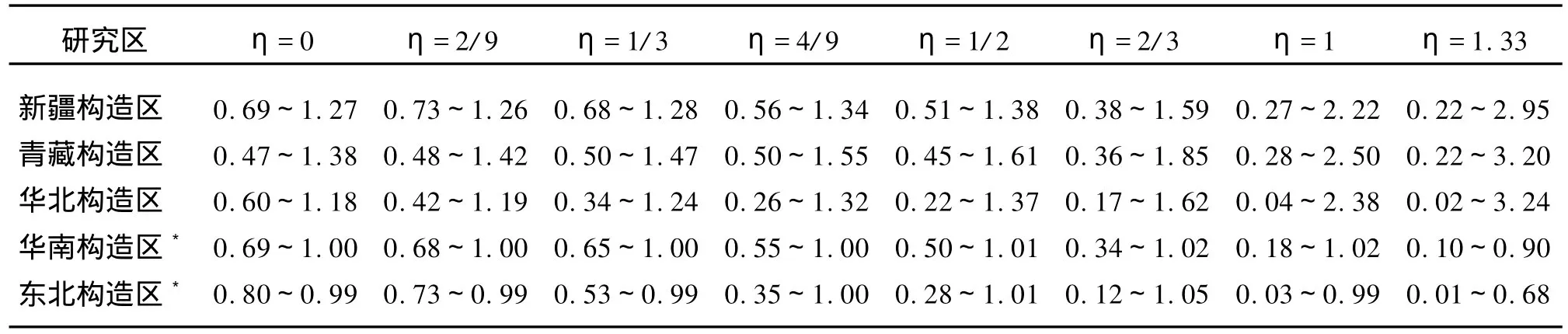
表4 各构造区广义地震应变释放时间分布 Hölder奇异指数α的存在范围表

由于每个采样时间段内均保证样本的存在性,表3中在各构造区η取不同的值时,D0均接近或等于1是可以理解的(表3中 D0的个别估值为0.998的近似),和容量维的定义是一致的。同一构造区内,η取不同的值时,多重分形谱 Dq的估计值明显不同,总体上当η增加时Dq(q>0)的估计值将随之减小。对各构造区,当η取相同的值时其多重分形谱Dq估计值也有明显的差别,特别当η较大时。图2给出了各构造区 D1和η取值的关系曲线。图中可见,随着η取值的增加,新疆、青藏和华南构造区的D1估计值具有相对一致的逐步减小特征,表明这些构造区地震动强度时间分布的丛集性特征具有相似性;华北和东北构造区 D1随η取不同的值变化情况较为一致,表明两构造区地震动强度时间分布的丛集性特征相似。新疆、青藏和华南构造区的D1～η曲线相对于华北、东北构造区的情况差异较大,表明中国西部、华南地区和华北、东北地区地震动强度时间分布的丛集性特征的差异。当η取较小的值时(如η<0.4)各构造区的 D1估计值差别不大。这些结果表明,研究区域地震活动强度时间分布的丛集特征时应考虑广义应变释放的重要性。若仅考虑地震活动频度、Benioff应变或地震矩,难免得到片面的结论。

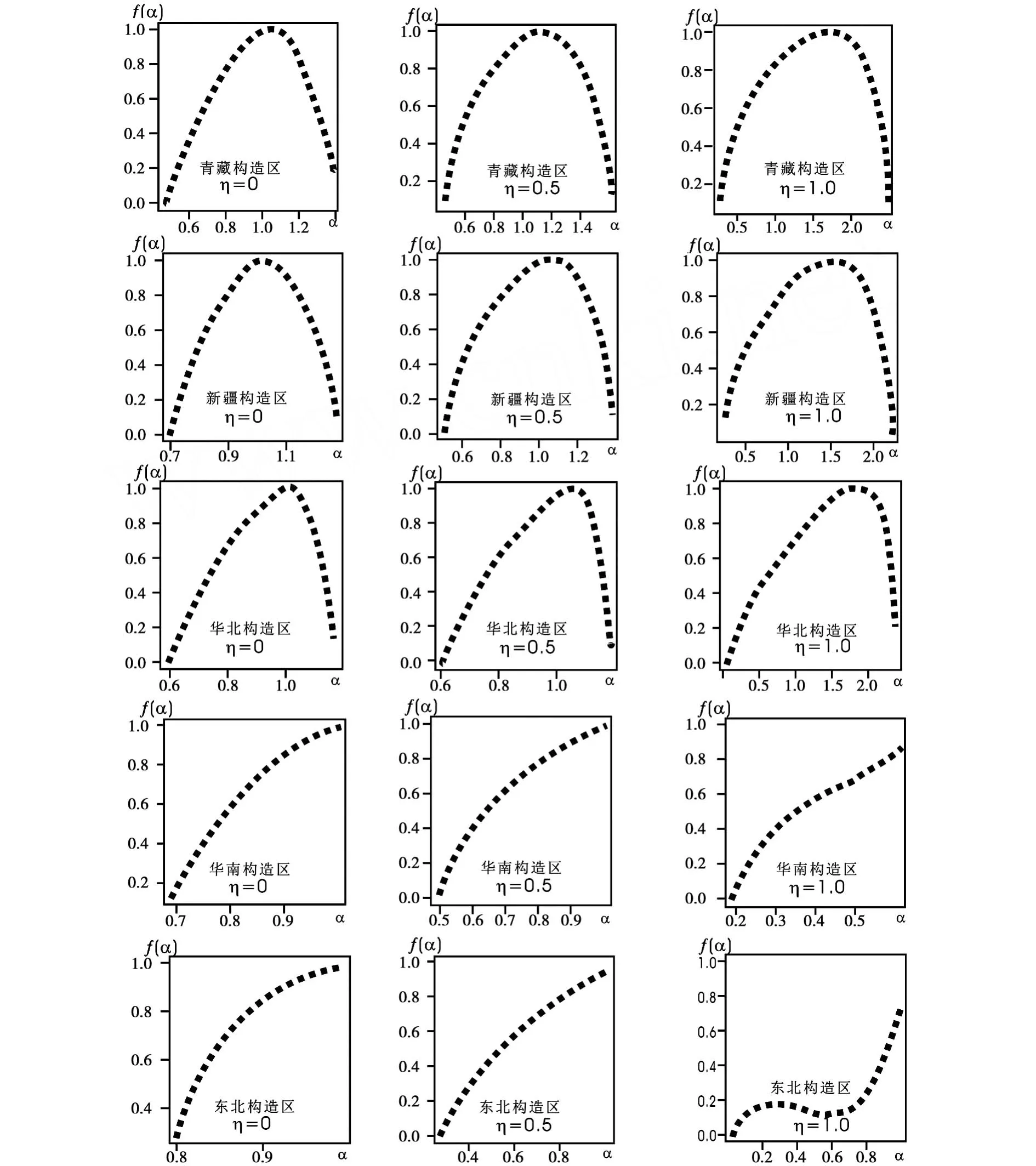
图1 各构造区η取不同值时地震活动时间分布f(α)～α曲线图

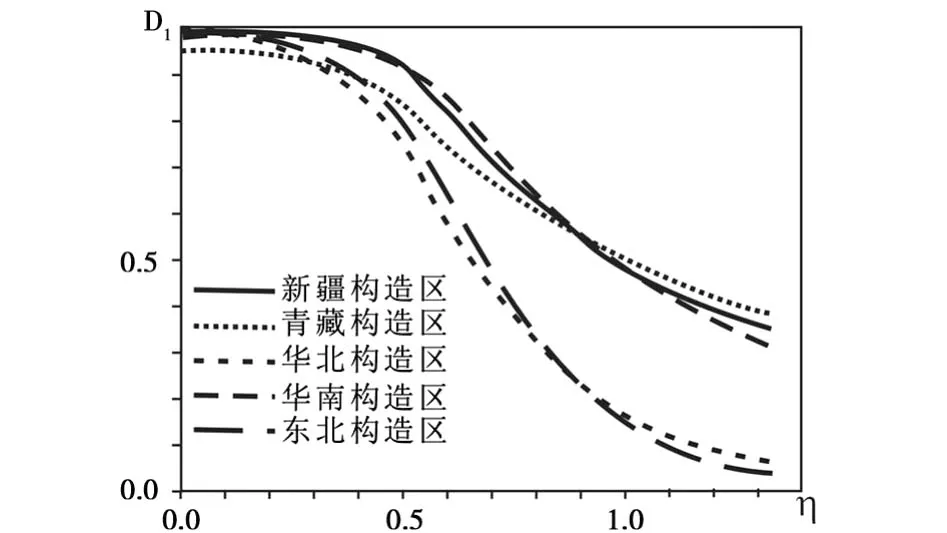
图2 中国大陆各构造区η和D1关系曲线图

多重分形奇异谱 f(α)和 Hölder奇异指数α的存在范围也随η及构造区的不同而变化。对新疆、青藏和华北构造区而言,在α的存在范围内 f(α)为一非对称光滑连续的钟形曲线。计算结果显示,对上述各构造区多数情况下¯α-α(D0)小于0,曲线在α的存在范围内偏向于右侧,表明具有稀疏性质的“观测”(广义应变释放)出现的频度小于具有丛集性质的“观测”出现的频度,“稀疏”集合的测度范围小于“丛集”集合的测度范围,“丛集”成为地震活动的主要特色。α的存在范围随着η取值的增加而逐步变大(表4),显示“稀疏”—“丛集”的差异增加。此外,f(α)～α曲线的歪斜程度随η的变化也有一定的变化,新疆构造区在η<1/3时、青藏构造区在η为1/3和4/9时 f(α)～α曲线接近于对称分布,表明新疆构造区中小地震活动、青藏构造区中等地震活动时间轴上的丛集—稀疏分布具有一定均匀性。华北构造区 f(α)～α曲线无论η取值大小均明显向右歪斜,表明本区小震、强震活动的丛集性均显著。

图3绘出了新疆、青藏和华北构造区η和α关系曲线,数据取自表4。图中可见,新疆构造区α的存在范围在η取不同值时均窄于青藏地区,但2构造区α的存在范围随η的变化趋势基本相同。在η取较小值时(新疆构造区η<1/3、青藏构造区η<4/9)2构造区α的存在范围随η的变化很小,但η取较大值时α的存在范围随η的增加而非线性的增加,表明强震活动的丛集性较小震活动的丛集性层次显著丰富。华北构造区α的存在范围随η的变化不同于新疆和青藏地区。图3显示,无论η取值大小,α的存在范围随η的增加而非线性增加现象显著,表明华北构造区地震活动丛集性无论小震和中强地震均有丰富的层次性。

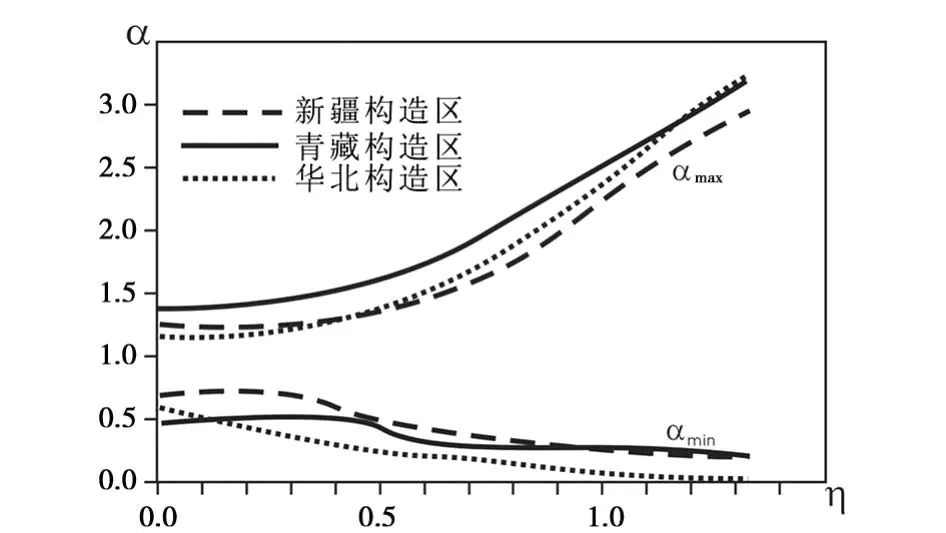
图3 新疆、青藏和华北构造区η和α关系曲线图

表4和图3可见,在η取较小值时新疆构造区αmin大于青藏构造区的情况,表明重视小地震活动时,新疆构造区地震活动强度时间分布丛集程度最高部分的地震发生概率小于青藏构造区的情况。当在η取较大值时,2构造区αmin基本一致。新疆构造区αmax始终小于青藏构造区的情况,表明新疆构造区地震活动强度时间分布丛集程度最低部分的发生概率大于青藏构造区,显示新疆构造区地震活动的稀疏性特征比青藏构造区显著。

对华南和东北构造区,计算结果显示 f(α)～α曲线为半钟形曲线。由于计算过程中当q<0时出现溢出(无限)而无法得到右支曲线的结果。鉴于右支曲线表示数据的稀疏性,因此2构造区地震活动强度时间分布的稀疏性无法描述(具有无限稀疏性)。

华南和东北构造区地震活动强度时间分布的丛集性特征也比较特殊。计算结果显示,对华南构造区η取2/3以下、东北构造区η取0.5以下时,丛集特征明显。当η取更大的值时,在 D0～D1间出现不连续现象,表明2构造区地震活动强度时间分布的特殊性。重视较小震级的地震活动时,丛集特征明显,而重视较大震级的地震活动时,丛集特征受到破坏。这可能和该2构造区地震活动水平较低有关。

图4为各构造区αmin随η的变化情况。图中可见,当η取较大值时αmin和华北构造区的结果接近,表明此种情况下东北地区丛集程度最高部分的强震发生概率和华北构造区相近,但丛集程度最高部分的小震发生概率小于华北构造区。同样,华南构造区小震丛集程度最高部分出现的概率和新疆构造区相似,但小于青藏构造区,而丛集程度最高部分的强震出现的概率大于新疆、青藏构造区且低于华北构造区。华北构造区和东北构造区强震成丛发生特征最为显著。

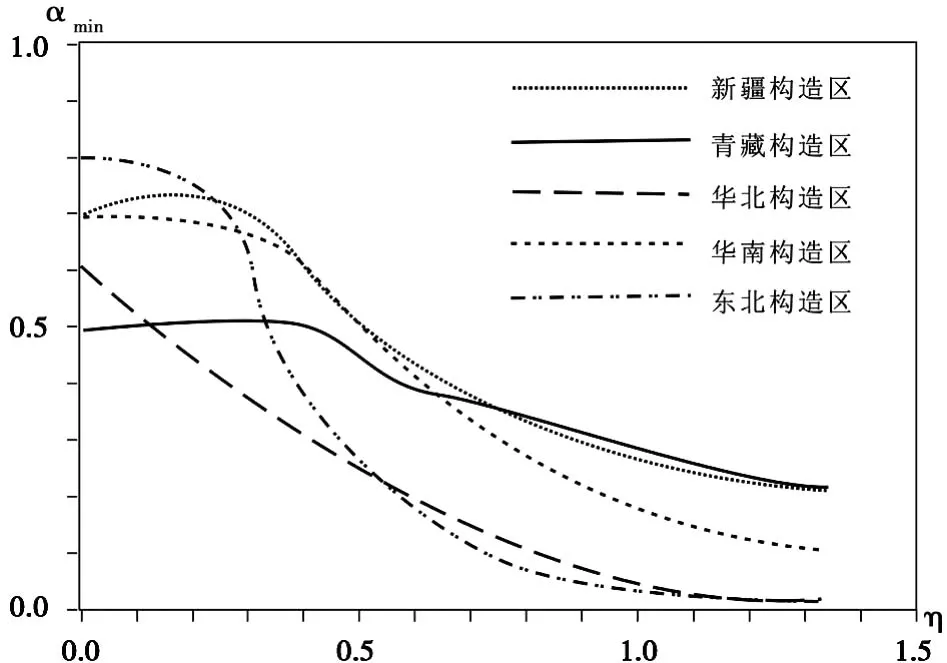
图4 各构造区η和αmin关系曲线图

3.2 中国大陆各构造区广义地震应变释放空间分布的多重分形特征

为研究地震活动强度空间分布丛集特征,首先需将研究区域按不同的分辨率离散化。考虑各构造区面积以及计算方便,研究中将新疆、青藏和东北构造区使用25×25km2、华北和华南构造区使用20×30km2的矩形方块网格进行离散化,计算各网格内所选资料的广义地震应变释放,进而计算广义应变空间分布的多重分形谱维数和多重分形奇异谱。

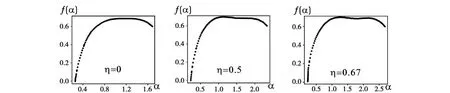
图5 新疆构造区η取不同值时地震活动空间分布f(α)～α曲线图

在η取不同值时计算了各构造区地震活动广义应变释放空间分布的多重分形奇异谱。作为示例,图5给出了关于新疆构造区的部分结果。根据计算,得到了q取不同值时的多重分形维数谱,表5列出了 D0、D1的估计值。表中可见,当η取不同值时新疆、青藏和东北构造区地震活动广义应变释放空间分布容量维均为0.687,华北、华南构造区其容量维均为0.722,表明地震活动广义应变释放在空间分布上具有相同的分形特征,和普通分形的容量维计算方法得到的结论一致。表5显示,随着η的增大,多重分形谱维数q>0分支有逐渐减小的趋势,表明越是强震,其空间分布的成丛性越弱。相反,当q取负值时,Dq广泛存在且逐渐增大,表明地震活动具有空间稀疏分布特征,且对于强震更加明显。这从计算得到的多重分形奇异谱 f(α)曲线向左极度歪斜的形态以及 Hölder奇异指数的存在范围也可看出。当q取正值时,除华南构造区外,各构造区Hölder奇异指数的存在范围很小(多重分形奇异谱的左支),表明丛集程度最高的地震活动强度空间分布存在的测度范围很小,接近于不考虑丛集性的普通分形分布的测度,即丛集性是十分有限的。当 q取负值时这些构造区 Hölder奇异指数的存在范围很大,多重分形奇异形钟形曲线的右支在右侧无界,表明地震活动强度空间分布具有无限稀疏性。华南构造区较为特殊,多重分形奇异谱仅有左支曲线,而右支曲线在本研究中无论η取什么值,由于计算溢出而未能显示,表明地震活动空间分布相对于其他构造区的特殊性。

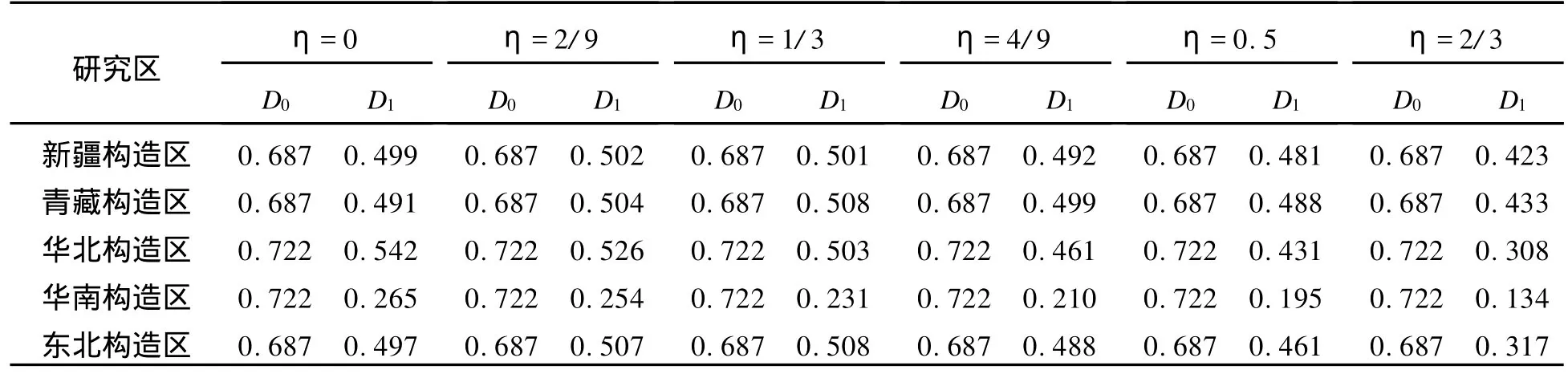
表5 各构造区地震活动广义应变释放空间分布多重分形谱维数估计值表

由于 Hölder奇异指数右侧无界,无法定量讨论α的存在范围,但可得到 f(α)曲线左支的存在范围αmin-α(D0),表6和图6给出了新疆构造区、青藏构造区、华北构造区、华南构造区和东北构造区的αmin、α(D0),(简记为α0)值随η的变化情况。

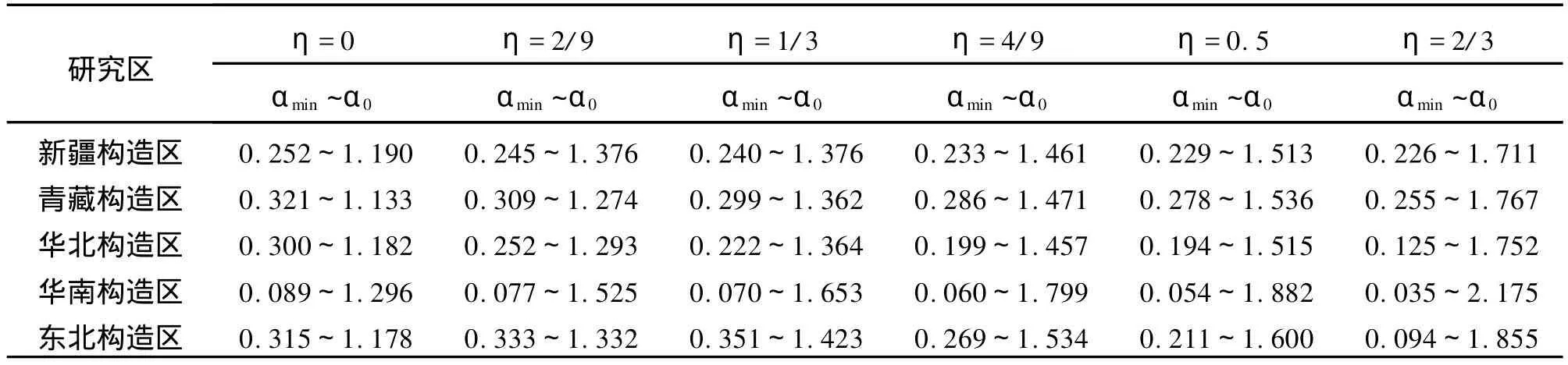
表6 各构造区地震活动广义应变释放空间分布 q≥0时 Hölder奇异指数存在范围表

图6中可见,对各构造区αmin总体上随η增加逐渐变小,α0则逐步变大,体现了地震活动频度、震源破裂线度、震源破裂面积等丛集特征的不一致性,进而体现地区构造和地震应力场的复杂性。图6显示,新疆和青藏构造区αmin、α0总体上随η的变化趋势较为一致,表明2构造区不同强度地震空间分布的丛集特征总体相似。但也有一定的区别,从表6和图6可见,新疆构造区相对青藏构造区不同强度地震最密集部分的出现概率均大于青藏构造区,小震—中强地震密集程度最低部分丛集出现的概率小于青藏地区,强地震密集程度最低部分丛集出现的概率则大于青藏构造区。说明新疆构造区强震空间分布较青藏构造区密集,且密集程度最低的丛集存在区域多于青藏构造区、小震空间分布也较青藏构造区密集,但密集程度最低的丛集存在区域较青藏构造区少,青藏构造区存在更多密集程度低的小震空间分布丛集区。华北构造区中小地震空间分布最密集部分的出现概率略大于青藏构造区、略小于新疆构造区,但强震空间分布最密集部分的出现概率均大于新疆和青藏构造区,表明强震空间分布较青藏和新疆构造区更为集中。华北构造区地震空间分布密集程度最低的丛集区空间分布和青藏、新疆构造区相当。华南构造区地震空间分布最密集部分的出现概率明显大于其他各构造区,密集程度最低的丛集区域出现的概率明显小于其他各构造区,说明华南构造区仅部分区域存在地震活动空间分布丛集。东北构造区中小地震空间分布最密集部分出现的概率略小于新疆、青藏和华北构造区,但强震空间分布最密集部分的存在概率大于新疆和青藏构造区,和华北构造区相当,比华南地区小。密集程度最低部分的存在概率小于新疆、青藏、华北构造区,但大于华南构造区。各构造区αmin-α(D0)范围随η增加而加大,表明随着地震强度的增强,地震活动空间分布的丛集性差异逐步变大,体现出随着震级增加地震活动在某些地区集中的特征。

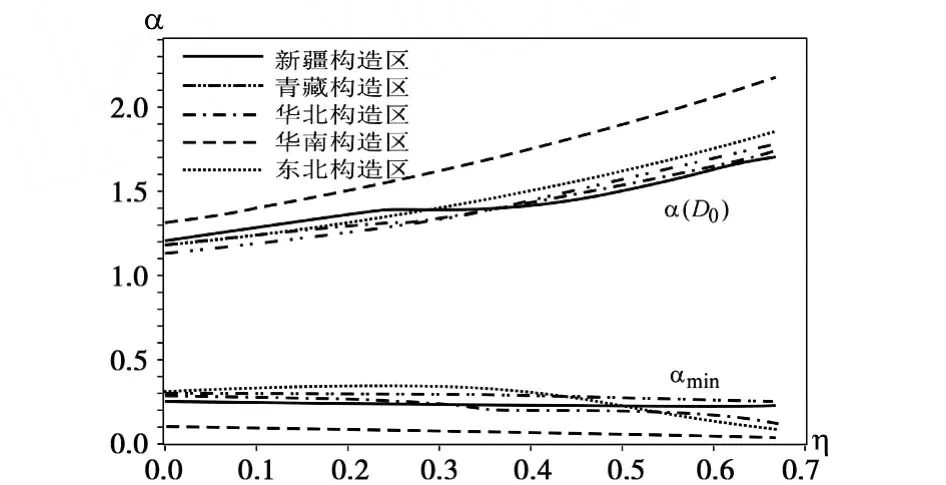
图6 各构造区η与α关系曲线图

4 结论与讨论

依据多重分形分析方法,对中国大陆各构造区地震活动广义应变释放时间、空间分布的多重分形特征进行了分析。关于地震活动广义应变释放时间分布的研究表明,随着η的变化,在q取正值时各构造区多重分形谱维数Dq的估计值总体上有减小的趋势,当q取负值时Dq则逐渐增大,但变化趋势不尽相同(分为2组)。其中,东北、华北构造区 Dq的变化趋势基本一致,华南、青藏和新疆构造区 Dq的变化趋势基本相似。相比之下,在 q取正值时,东北、华北构造区多重分形谱维数 Dq比华南、青藏和新疆构造区减小的速度更快,特别当η取较大值时。各构造区多重分形奇异谱 f(α)～α曲线形态差异很大,华北、青藏和新疆构造区多重分形奇异谱 f(α)～α为向右歪斜的非对称光滑钟形曲线,但青藏和新疆构造区在η取较小值时基本对称,而华北构造区无论η取较大或较小值均为非对称;华南和东北构造区在η取较小值时为左侧半钟形曲线,当η取较大值时,半钟形曲线也受到破坏,表明2构造区强震时间分布的特殊性。

各构造区地震活动空间分布丛集性也存在明显差异。随着η的增加,青藏和新疆构造区地震活动广义应变释放空间分布的多重分形谱维数Dq具有相似的取值且变化较小,华北、华南、东北构造区多重分形谱维数Dq(q>0)减小速度较快。此外,在η取值相同时华南构造区Dq除D0外与上述各构造区均有较大差异。除华南构造区外,各构造区αmin、α0总体上随η的变化趋势较为一致,但也有一定的区别,特别当η取较大的值时。华南构造区αmin、α0的取值范围明显大于其他构造区,新疆、青藏、东北和华北构造区αmin、α0的取值范围在相同的η时差异不大。多重分形奇异谱 f(α)～α的曲线形态特征在各构造区不尽相同,特别是华南构造区,与其他各构造区有显著差异。

广义地震应变释放时间空间分布的多重分形特征可以向人们揭示较多、较全面的地震活动在时间和空间分布上的差异。对其进行深入研究并应用于对未来的强震预测中是有益的。笔者曾以1976年唐山7.8级地震、1989年大同—阳高6.1级地震、1999年台湾集集7.3级地震等为例对这一问题进行过探索,得到了一些有意义的结论[3-4,11]。限于本文的研究目的和篇幅,这里对这一问题不做进一步地讨论。

[1] 朱令人,周仕勇.地震多重分形标度指数谱 f(α)的研究[J].西北地震学报,1992,14(2):30-35.

[2] 安镇文,杨翠华,王琳英,等.地震时空丛集的多重分形研究[J].地球物理学报,2000,43(1):74-80.

[3] 陈时军,David Harte,王丽凤,等.广义地震应变能释放的多重分形特征[J].地震学报,2003a,25(2):182-190.

[4] 陈时军,马丽,王丽凤,等.强震前后广义地震应变释放过程的丛集特征[J].地震,2003b,23(2):29-38.

[5] Hooge C,Schertzer D,Malouin J F,et al.Multifractal Phase Transition:the Origin of Self-organized Criticality in Earthquakes[J].Nonlin.Proc.Geophys.1994,1:191-197.

[6] Godano C,Alonzo M L and Vilardo G.Multifractal Approach to Time Clustering of Earthquakes,Application to Mt.Vesuvio Seismicity[J].PAGEOPH.1997,149:375-390.

[7] Harte D.Multifractals:Theory and Application[M].New York:Chapman&Hall/CRC Press.2001,29-46,127-194.

[8] Heinz-Ottto P,Hutmart J and Dietmar S.Chaos and Fractal-New Frontiers of Science[M].New York:Springer Velay,Hamilton Printing Co.Rennselaer.1997,921-954.

[9] Chhabra A B,Meneveauc,Jensen R V and Sreenivasan K R.Direct determination of thef(α)singularity spectrum and its application to fully developed turbulence[C]//Phys.Rev.A:At.,Mol.,Opt.Phys.1989,40:5284-5294.

[10] Harte D.Document for the Statistical Seismology Library,In:School of Mathematics and Computing Sciences[R].Wellington:Victoria University of Wellington press.2004,1-162.

[11] 陈时军,孙龙梅,马丽.板内与板间地震活动时空分布的多重分形特征研究[J].地震学报,2007,29(1):38-47.

Multifractal Features of Spatial-Temporal Distribution of Earthquakes in Chinese Mainland

CHEN Shi-jun1,DU Li-ying1,WEI Xu-yun2
(1.Earthquake Engineering Research Center of Shandong Province,Jinan 250014;
2.Library of the Affiliated Hospital of Shandong University of Traditional Chinese Medicine,Jinan 200021)

In this paper,we explored multifractal features of spatial-temporal distribution of seismic general strain release of earthquakes in tectonic regions in Chinese mainland respectively.Results show that these multifractal features in different tectonic regions are apparently distinct from each other.

Chinese mainland;seismicity;spatial-temporal distribution;multifractal

P315.5

A

1003-1375(2010)04-0001-08

2010-02-23

地震科学联合基金资助项目(编号:106085)

陈时军(1963-),男(汉族),河南虞城人,研究员,主要从事地震工程、地震活动性、大地测量等方面的研究.E-mail:chenshijun@seis.ac.cn