系泊模式对深水Spar平台运动性能的影响*

孙金伟,王树青

(中国海洋大学工程学院,山东青岛266100)

系泊模式对深水Spar平台运动性能的影响*

孙金伟,王树青

(中国海洋大学工程学院,山东青岛266100)

在频域和时域内研究对等分布式系泊和分组式系泊2种系泊模式对Spar平台运动性能的影响,并分析单根系泊缆破断失效后平台运动性能的变化。首先建立Spar平台的三维水动力模型,通过在平台柱体导缆孔处指定预张力、倾角和刚度来模拟系泊系统的影响;然后采用三维势流理论进行浮体水动力计算,获得Spar平台运动响应的传递函数等水动力参数;最后根据实际海况资料,在平台生存工况下,进行Spar平台在完好系泊和单根系泊缆破断失效状态下运动响应的短期预报,并在时域内进行耦合分析,研究平台运动响应和系泊缆张力变化情况。研究结果对Spar平台系泊系统设计和平台设计前期运动性能研究有参考意义。

深水;Spar平台;运动性能;系泊模式;短期预报;时域分析

随着工业的发展,当今世界大部分地区的浅海油气资源已日趋减少,海洋油气开发由近海向深海发展已成必然趋势。在深海和超深海油气开发中,深海浮式平台发挥着越来越重要的作用。单柱式平台(Spar)是深海采油较常用的浮式平台,其特点是吃水深,重心很低,波浪对其影响较小,相对而言在恶劣的海况下具有良好的稳定性;同时Spar造价低、便于安装、可重复使用,其柱体内部可储油,而大吃水柱体对立管有良好的保护作用;平台的运动响应对水深变化不敏感,更适宜于在深水海域应用。Spar平台靠系泊系统固定在工作海域进行作业,慢变的波浪、风、流载荷使系泊浮式平台产生较大的低频慢漂运动,波频运动使系泊系统产生显著的动力响应,而不同的系泊模式对平台的运动性能有较大的影响,因此在Spar平台设计前期,有必要对不同形式的系泊模式展开研究。

近年来,关于深水浮体水动力性能方面的研究较多,而考虑系泊模式对浮体运动性能影响的研究则相对较少。WANG Ying[1]等在频域和时域内研究了1种新型Spar平台—Geometric Spar的水动力性能,考虑了浮体与立管及锚泊系统的耦合影响。童波[2]等探讨了半潜式平台悬链线式系泊系统下,系泊缆直径、长度和预张力角度以及系泊缆布置角度和系泊缆数目对于锚泊系统动力响应的影响。王世圣[3]等应用SESAM软件研究了4种深水半潜式钻井平台的运动性能,应用频域分析法对深水半潜式钻井平台运动响应进行了短期预报。潘子辉[4]应用MOSES软件对一座工作海域为我国南海的深海半潜式钻井平台的运动响应进行了分析,并进行了试验验证。陈徐均[5]等对单一锚链的锚泊系统,基于线性化假设推导了不同布链方式下交叉型和人字型锚链系统提供的首摇和横摇回复力矩的大小以及方向的不确定性。T.M.Smith[6]通过计算发现随着位移的增大,锚泊线夹角为22.5～67.5(°)的锚泊系统布置方式的系统回复力显示出方向上的平稳性。

关于深水浮式平台水动力性能的研究,通常采用数值模拟和模型试验相结合的方法。但是,模型试验对水池的水深有较高要求,国内能够开展模型实验的单位和机构并不多,模型试验在条件上存在着一定的限制;国内外某些文献有平台模型试验或现场实测的数据,但通常缺乏平台具体的尺寸参数,在数模的建立上存在难度,因此要做到数值模拟和模型试验相结合还存在一定困难。本文主要采用数值模拟的方法来开展研究。DNV船级社的SESAM软件是海洋工程界较成熟的商业软件,其HYDROD和DEEPC模块分别针对频域内水动力特性计算和时域内耦合分析,被证明可信度较高,本文主要采用此软件作为数值分析的工具。

本文在频域和时域内研究了对等分布式系泊和分组式系泊2种系泊模式对Spar平台运动性能的影响,并分析了单根系泊缆破断失效情况下平台运动性能的变化情况。频域内以三维势流理论为基础计算Spar平台的水动力特性,建立Anchor单元模拟系泊缆的预张力、倾角及回复刚度等,计算了浮体的运动特性,并进行了运动响应的短期预报;时域分析考虑了锚泊系统与浮体的耦合作用,结合频域水动力参数,建立Spar平台和锚泊系统的耦合模型,进行了非线性时域模拟分析[7],获取了浮体运动特性和系泊缆张力结果,综合比较频域和时域分析结果,得出了有意结论。

1 计算相关理论

1.1 三维势流理论

海洋工程结构中,对于一个在波浪场中微幅运动的大尺度结构物来说,波浪载荷对结构的作用可分为绕射作用和辐射作用2部分,Spar平台承受的波浪载荷为波浪绕射载荷和辐射载荷的叠加。

势流理论是目前最常用的计算结构物湿表面上波浪力的方法,它设定速度势存在并满足拉普拉斯方程和四类边界条件:自由面条件、海底条件、物体湿表面条件和辐射条件(无穷远处边界条件)。根据拉普拉斯方程和边界条件可以唯一地确定出速度势,然后按伯努利公式计算物体湿表面上的压力。作为浮体在波浪上运动的流体动力问题,关键是求流场中的速度势。流场中的总速度势应包括入射波的贡献、浮体存在对流场扰动的贡献和浮体运动对流场扰动的贡献。即

式中:Φ为流场总速度势;ξj指刚体假定下浮体6个自由度运动的幅值;Φj为单位辐射势;Φ0为入射势,Φ7为单位绕射势,表示浮体存在对流场扰动的贡献,二者相加得到总绕射势ΦD。

辐射速度势和绕射速度势满足物面边界条件:

选择自由面源势作为格林函数,通过格林定理求解上述边界条件,即可得到总速度势Φ,进而求出物体表面上的压强分布,求得作用在物体上的波浪力与力矩。

1.2 运动方程

考虑系泊系统的平台运动方程:

式中:M为浮体的广义质量矩阵;μ、λ和K分别为附加质量矩阵、阻尼系数矩阵和静水回复力矩阵;{、{和{x}分别为广义加速度列阵、广义速度列阵和广义位移列阵;Ffk为佛汝德一克雷洛夫力;Fd为波浪绕射力;Fw为风力;Fc为流力;Fm为系泊力。

考虑系泊力和环境载荷等非线性因素的影响,本文采用间接时域法即先求出频域水动力参数,如附加质量、阻尼以及波浪力,通过FFT将计算结果从频域变为时域。运动方程如下:

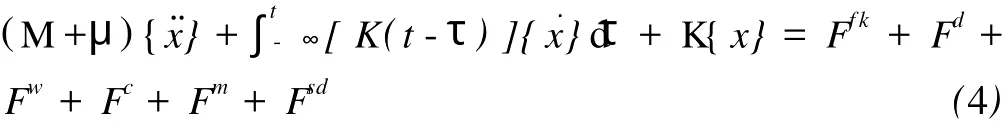
式中:K(t-τ)为系统的延迟函数;Fsd为二阶波浪漂移力;其他参数含义同式(3)。

2 模型建立及水动力分析

2.1 系泊缆布置

系泊缆采用锚链-钢缆-锚链三段式材料,采用悬链线式连接,锚链的轴向刚度为1.03×106kN,直径为0.2156 m,钢缆的轴向刚度为3.19×105kN,直径为0.1654 m。系泊方式考虑对等分布式系泊和分组式系泊2种。对等分布式系泊模式中,12根系泊缆沿Spar平台四周均匀分布,相邻两系泊缆间的夹角为30(°),见图1;分组式系泊模式中,12根系泊缆分成4组,每组3根系泊缆,4组系泊缆沿Spar平台四周均匀分布,相邻两系泊缆组之间的夹角为90(°),每组系泊缆内,相邻两系泊缆之间的夹角为22.5(°),见图3。2种系泊模式中,系泊缆与海平面的夹角均为42(°)。本文还考虑了锚泊系统中编号为1的系泊缆破断情况,2种系泊模式下1号系泊缆破断失效系泊示意图分别见图2和图4。

图1 对等分布式系泊Fig.1 Equally distributed mooring method

图2 对等分布式系泊(1号系泊缆破断)Fig.2 Equally distributed mooring method(with mooring line 1 broken)

图3 分组式系泊Fig.3 Grouped mooring method

图4 分组式系泊(1号系泊缆破断)Fig.4 Grouped mooring method(with mooring line 1 broken)

2.2 有限元模型

Spar平台柱体直径为37.18 m,生存状态下,吃水198.12 m,平台排水体积为215 164 m3。建立计算所需的平台湿表面模型(见图5)。通过定义重心位置和惯性矩半径来反映平台的总布置,在平台柱体表面周围,建立Anchor单元以模拟系泊缆的影响,单根系泊缆的水平回复刚度为90 kN/m,竖向回复刚度为66 kN/m,对等分布系泊模式中所有系泊缆的初始预张力为1 639.81 kN,分组系泊模式中1、4、7和10号系泊缆的初始预张力为1 639.81 kN,其余系泊缆的初始预张力为1 796.81 kN。据经验估算,取7%临界垂荡阻尼以考虑平台及锚泊系统的黏性阻尼。

图5 Spar平台湿表面模型Fig.5 Panel model of Spar

2.3 水动力分析

Spar平台所在海域水深1 500 m,海水密度1 025 kg/m3,重力加速度9.8 m/s2。考虑到Spar平台的对称性,计算平台的动力响应时,选取规则波浪的入射方向共4个,角度为0,30,60和90(°),波浪周期从4～33 s,间隔为1 s。图6～图11给出了波浪30(°)入射时,2种系泊模式在完好系泊和1号系泊缆破断失效情况下,浮体在垂荡、纵摇、横摇、纵荡、横荡和首摇6个自由度上的运动响应RAO。

从图6～11可知,2种系泊模式的完好系泊状态下,浮体在各自由度上的运动响应比较接近;对于2种系泊模式,1号系泊缆破断前后,浮体在垂荡、纵摇、横摇、纵荡和横荡5个自由度上的运动响应没有明显变化,而浮体首摇运动响应值在1号系泊缆破断后较完好系泊时有所增大,但增大数值较小。

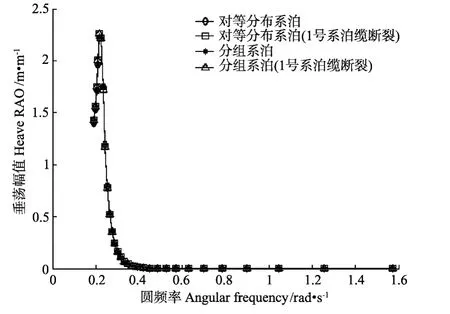
图6 垂荡响应RAOFig.6 Heave RAO

图7 纵摇响应RAOFig.7 Pitch RAO

图8 横摇响应RAOFig.8 Roll RAO

图9 纵荡响应RAOFig.9 Surge RAO

图10 横荡响应RAOFig.10 Sway RAO

图11 首摇响应RAOFig.11 Yaw RAO

3 Spar平台运动响应的短期预报

应用水动力分析中得到的Spar平台运动响应的传递函数,结合由平台作业海域海况资料确定的海浪谱,可以得到相应的平台运动响应谱,从而用谱分析方法预报不规则波中Spar平台的短期运动响应[8-9]。为计算方便,本文仅考虑了平台在某海域生存工况下的运动响应。短期预报中的海浪谱为JONSWAP谱,生存工况下,有效波高为12 m,零跨周期为13 s,尖度因子为3.3。计算时间为3 h,得到平台运动极值响应的短期预报值,见表1。

由表1可知,对等分布式系泊和分组式系泊的完好状态相比较,对等分布式系泊在纵荡和横荡2个自由度上的运动响应比分组式系泊要小,其他自由度的运动响应则比较接近;无论是对等分布式系泊还是分组式系泊,在1号系泊缆破断前后,平台在各自由度上的运动响应变化很小。需要注意的是,频域分析中系泊缆的系泊力和浮体所受的环境载荷等非线性因素都进行了线性化的处理,因此,频域内的分析预报只能大体上预估浮体运动响应,还需进一步进行时域分析加以校检。

4 Spar平台的时域耦合分析

4.1 时域内Spar平台运动响应

为了更好的考虑系泊力和环境载荷等非线性因素的影响,本文以频域内分析得到的水动力参数为基础,进行了Spar平台的时域耦合分析,环境条件同频域分析,计算时间长为3 h。得到2种系泊模式的完好状态和1号系泊缆破断失效情况下,Spar平台的运动响应极值和各系泊缆张力极值,分别见表2和3。

由表2可知,完好状态下,对等分布系泊模式在垂荡、纵摇、横摇和首摇4个自由度上的运动响应值接近于分组系泊模式,而在横荡和纵荡的运动响应则小于分组系泊模式。以0(°)方向上浮体纵荡响应为例,对等分布系泊模式下响应最大值为9.162 6 m,小于分组系泊模式下的9.717 4 m。2种系泊模式下的完好状态与1号系泊缆破断失效情况相比,完好状态下,对于2种系泊模式而言,各自由度上的运动响应要略小于1号系泊缆破断情况,这在纵荡、横荡和首摇方面表现的比较明显。仍以波浪0(°)方向上浮体纵荡响应为例,对等分布模式的完好系泊情况下,Spar平台的纵荡偏移量为17.421 6 m,而在1号系泊缆破断后,纵荡偏移量变为19.685 9 m。

由于波浪力是引起平台垂荡运动的主要因素,所以2种系泊模式在频域和时域内的垂荡值相差不大,而在1号系泊缆破断后,系泊缆提供的垂向回复刚度变小,浮体的垂荡响应值则稍微有所增大,但变化值很小;频域内横荡和纵荡值略小于时域内计算结果,这是因为在时域计算中考虑了波浪的二阶定常慢漂力的作用,浮体的静态平衡位置产生了一定偏移;在纵摇和横摇的计算方面,频域结果比时域要小许多,这是因为时域内的计算考虑了波浪的二阶力矩作用,以及垂荡与横摇和纵摇的耦合作用,导致时域结果大于频域结果,但频域和时域分析结果的总体趋势是一致的。

表1 频域内Spar平台运动极值响应短期预报Table 1 Short term response of Spar platform in frequency domain analysis

表2 时域内Spar运动响应极值Table 2 Extreme response of Spar platform in time domain analysis

表3 时域内系泊缆张力极值Table 3 Extreme tension of mooring lines in time domain analysis

4.2 系泊缆张力结果

破断的1号系泊缆的投影是在X轴线上,因此对平台来说最为危险的波浪入射方向是0(°)。表3列出了波浪0(°)入射时,2种系泊模式在完好状态和1号系泊缆破断情况下的系泊缆张力极值。

由表3可知,在2种系泊模式的完好系泊状态下,分组式系泊模式中的1和7号系泊缆张力略小于对等分布式系泊模式下中对应系泊缆张力,而其他各系泊缆张力均要大于对等分布式系泊模式下的系泊缆张力,其中6和8号系泊缆张力增加最大,增加量为9.14%;对于对等分布式系泊,完好状态下,7号系泊缆的张力最大,在1号系泊缆破断后,1号系泊缆两侧的2和12号系泊缆的张力变为最大,其张力增加量也为最大,为17.36%;对于分组式系泊,完好状态下6和8号系泊缆的张力最大,在1号系泊缆破断后,1号系泊缆两侧的2和12号系泊缆和的张力变为最大,其张力增加量也为最大,为18.76%。

结合Spar平台在时域内的运动响应和各系泊缆张力分析结果,可以得出,对等分布系泊下浮体运动性能要优于分组系泊。但在实际工程中,系泊模式的选择则还要考虑到具体的海洋环境、海底地形地貌、立管布置以及油田开采模式等各方面因素的影响。

5 结论

本文在频域和时域内研究了对等分布式系泊和分组式系泊2种系泊模式对Spar平台运动性能的影响,得出以下结论:

(1)在相同的浮体几何形状、主尺度和质量分布情况下,频域内系泊模式对平台运动性能的影响主要体现在系泊缆对浮体运动性能的影响。计算结果表明,在系泊缆回复刚度和初始预张力相近的情况下,2种系泊模式对浮体的运动性能的影响比较接近。

(2)时域内计算结果表明,对等分布式系泊模式下大多数系泊缆的张力要小于分组系泊模式,在浮体运动响应方面,对等分布式系泊模式略优于分组系泊模式;1号系泊缆破断后,浮体在各自由度上的运动响应以及大部分系泊缆的张力均有所变大,其中分组系泊模式下的系泊缆极值张力增加量要大于对等分布模式。

(3)时域分析考虑了系泊力和环境载荷等非线性因素的影响,分析预报更加准确,是对频域分析结果的进一步验证。

(4)综合考虑浮体运动响应和系泊缆张力结果,可知对等分布式系泊模式要优于分组系泊模式。

[1] Wang Ying,Yang Jian-min,Hu Zhi-qiang,et al.Theoretical research on hydrodynamics of a geometric Spar in frequency and timedomains[J].Journal of Hydrodynamics,2008,20(1):30-37.

[2] 童波,杨建民.深水半潜平台悬链线式系泊系统耦合动力分析[J].中国海洋平台,2008,23(6):1-7

[3] 王世圣,谢彬.3 000米深水半潜式钻井平台运动性能研究[J].中国海上油气,2007,19(4):277-280.

[4] 潘子辉.深海半潜式钻井平台运动响应预报与分析[J].船舶,2008,(1):32-36.

[5] 陈徐均,汤雪峰.系泊浮体布链方式优劣的理论分析[J].河海大学学报,2001,29:84-87.

[6] Smith T M,Chen M C,et al.Systematic data for the preliminary design of mooring systems[C].Proceedings of the fourth International Offshore Mechanics and Arctic Engineering Symposium,1985,1:403-407.

[7] Deep water coupled floater motion analysis[S],2005.

[8] Wadam Sesam User ManuAL/[M].Norway:Det Norske Veritas,2005:2-10.

[9] 黄鹿祥,陆鑫森.海洋工程流体力学及结构动力响应[M].上海:上海交通大学出版社,1992:4-25.

Study on Motion Performance of Deepwater Spar Platform Under Different Mooring Methods

The motion performances of Spar platform with equally distributed mooring method and grouped mooring method have been studied in both frequency domain and time domain,for both intact case and damaged case of one mooring line.First,3D hydrodynamic finite element model is built and the effects of the mooring system are taken into account by giving the specified pre-tension,angle and stiffness of the mooring lines on the fairleads.And hydrodynamic analysis of Spar platform is performed utilizing potential flow theory in order to calculate the hydrodynamic coefficients,such as the motion Response Amplitude Operators(RAO).Then,frequency domain analysis is applied to predict short term motion response for motion performance of Spar platform under the given extreme environmental conditions.At last,time domain analysis of the motion response of Spar is conducted for the coupled system and the tensions of mooring lines are calculated.The research results can be served as a reference for selecting the mooring methods and the performance study of preliminary design.

deepwater;Spar platform;motion performance;mooring methods;short term prediction;time domain analysis

SUN Jin-Wei,WANG Shu-Qing
(College of Engineering,Ocean University of China,Qingdao 266100,China)

TU312

A

1672-5174(2010)09-147-07

国家自然科学基金重点项目(50739004,50639030)资助

2009-11-26;

2010-02-15

孙金伟(1985-),男,硕士生,E-mail:sunjinwei@ouc.edu.cn

责任编辑 陈呈超