N 2分子电子振动光谱德兰德斯表的绘制及其分析

张岩文,张建军

N2分子电子振动光谱德兰德斯表的绘制及其分析

张岩文,张建军

(石河子大学生态物理重点实验室,石河子大学师范学院物理系,石河子832003)

为给光谱学的理论分析和实验研究提供参考依据,对N2分子电子振动光谱规律进行了的分析,并按照这些规律正确地指认了N2分子的电子振动光谱数据对应的量子数之间的跃迁,由此整理出了N2分子电子振动光谱的德兰德斯表,并通过对N2分子光谱波数的一次差值与二次差值的处理,获得了N2分子的电子振动常数。

N2分子;电子振动;光谱;德兰德斯表

通过研究分子光谱,可以获得分子结构、分子振动和转动的重要参数,但分子的光谱包含了电子能级间的跃迁、振动能级和转动能级间的跃迁,这样分子的光谱就变得非常复杂,因此如何正确地指认谱线的归属是一项比较复杂的工作。关于分子光谱和分子结构的许多专著中对此都有论述,但其分析过程非常简略,或者未展开分析[1～4]。

本文以N2分子为例,对此作重新整理和进一步的分析,力图以最简洁的方式分析N2分子电子振动光谱的数据,并快速准确地整理出N2分子电子振动光谱的德兰德斯表,进而求解出N2分子振动光谱常数,为光谱学的理论分析和实验研究提供参考。

1 N2分子电子振动光谱结构的分析

N2分子作为双原子分子,两个电子态之间的跃迁的光谱线波数[5]为:

式(1)中:σv为电子态光谱项对应波数,G(v)为振动光谱项,Fv(J)为转动光谱项,ve为平衡振动频率,veχe为非谐性系数,Bv为平衡转动常数,De为离心畸变常数。式(1)中带′的字母是指较高态,带″的字母是指较低态。

按照式(1),可以把光谱波数看作三个组成部分之和,对于给定电子态的跃迁,第1项电子态光谱项对应波数σe是一个常数,由于电子能级间隔最大,对应的光谱线波数也最大,故σe决定了电子谱线系在光谱中的位置。σr最小,它反映了光谱的转动精细结构,σv反映了本文主要考察的光谱的振动结构[6]。

一般 Fv(J)比 G(v)小得多,暂且略去σr(由 F(0)=F″(0)=0形成),即考察两个无转动态 F’(0)=F″(0)=0之间的跃迁[7],并由此讨论电子振动光谱。在这种情况下,光谱线波数化为

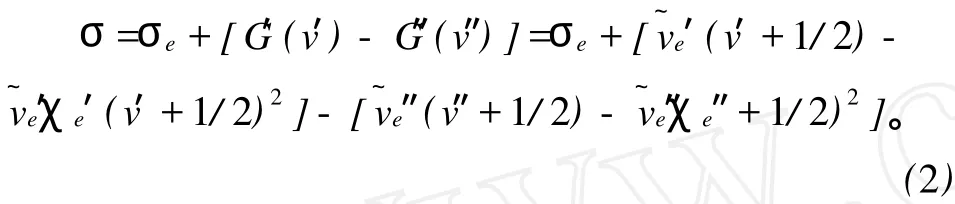
1.1 谱带序的排列规律

1.1.1 任意谱带序间的波数间隔

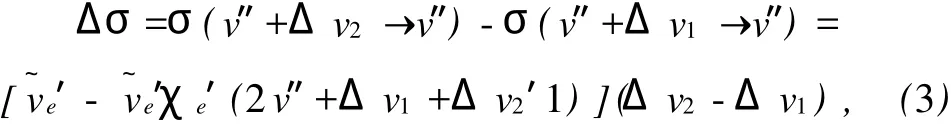
令式(3)中

Δv2-Δv1=1,

即得到相邻两谱带序的波数间隔为

由式(4)可以看出,相邻谱带序间的波数间隔,随Δv2=Δv1+1的增大而减小,即谱带序之间的间隔将随着Δσ的增大而逐渐减小。其二次差值为

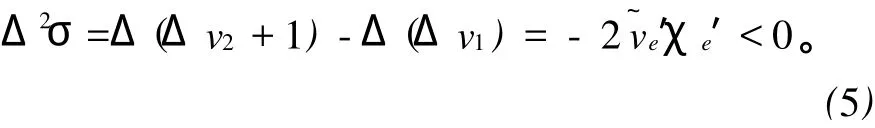
1.1.2 同一谱带序中相邻子带的波数间隔

在同一谱带序(Δv相同)中,相邻子带的量子数v′和v″之间刚好同时相差1故相邻两子带的波数间隔为

在 v″较小且略去非谐性项时,同一谱带序中的相邻两子带的波数间隔近似相等,波数间隔为Δσ=。由此可见,相邻子带波数间隔要远小于相邻谱带序的波数间隔,这正好反映了实际光谱带的特点,即光谱从Δv=0谱带序开始,Δv取负值时波数减小,谱带序向长波方向延伸,Δv取正值时波数增大,谱带序向短波方向延伸,而在每个谱带序的区域内(约为″),子带又近似以的间隔依次展开。

1.2 振动谱带前进带组的规律

电子振动谱带可以分解为如图1所示的两种前进组带:从同一个振动态 v′跃迁到不同的振动态v″所得到的的 v′前v″进带组;从不同的振动态 v′跃迁到固定的振动态v″所得到的 v″的v′前进带组。下面分别讨论两种前进带组的规律。

图1 代表前进带组的能级Fig.1 Energy level diagrams representing progressions of bands

1.2.1 从同一个振动态跃迁到不同的振动态 v″

由式(2)可知,从同一个振动态 v′跃迁到不同的振动态v″,其光谱线波数σ为

由上式可以看出,对于一定的电子态,G′(v′)为定值 ,故波数σ的变化规律与 G″(v″)相同 ,随着 G″(v″)(也就是v″)的增大而减小。相邻谱线波数间隔为:

其二次差值为

由式(9)可以看出,v′的 v″前进带组,相邻谱线波数间隔与 v′无关,而仅仅与 v″成线性关系,对于绝大多数分子,～v′χ′都大于 0,故随着 v″的增大 ,该ee波数间隔将减小。如在0的v″前进组中,(0,0)、(0,1)、(0,2)等谱线之间的间隔将会随 v″的增大而减小。对于不同的振动能级 v′的 v″前进带组,如(0,v″)、(1,v″) 、(2,v″)等等 ,其谱线间隔变化规律是相同的。

1.2.2 从不同的振动态 v′跃迁到固定的振动态v″

由式(4)可以得到由不同的态 v′跃迁到一个固定态v″态的谱线波数

对于一定的电子态,式中 G″(v″)是定值,所以σ的变化规律决定于 G′(v′)项 ,波数σ随 G′(v′)(即 v′)的增大而增大,与 v″前进带组的规律相反。此时相邻谱线波数间隔为

其二次差值为

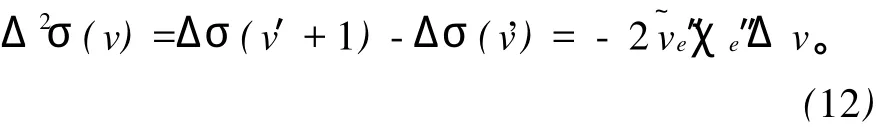
从式(12)可以看出,v′前进带组的谱线间隔变化规律与 v″前进带组相同 ,Δσ(v′)与 v′成线性关系 ,与v″无关。随着 v′的增大,相邻的谱线波数间隔将减小。如在0的 v′前进组中,(0,0)、(1,0)、(2,0)等谱线之间的间隔将会随 v″的增大而减小。

根据这些规律,可以检验后面将要列出德兰德斯表中数据位置是否正确,并估计数据的可靠性。在前进带组中,由相邻谱线的波数差公式(8)和前进带组中相邻谱线的波数差公式(11),可以确定振动结构参数~υe″χe″和~υe′χe′,~υe″和~υe′。

2 N2分子电子振动光谱对应量子数υ′、υ″的确定

υ′、υ″之间跃迁的具体数值见表1。

表1中σ所在列为N2分子的电子振动光谱波数[3],Δσ所在列为相邻谱带的波数差,Δ2σ所在列为二次差值。首先可以根据谱带序的规律,把它们划分为不同的谱带序当中,比如观察Δσ列中的数据,我们会发现这些数据被一个相对较大的数值分成了若干段,而且每一段中的数值从下向上基本都是递减的,说明在实际测量中只获得了每一个谱带序中相对较低的振动态之间跃迁谱线,所以在相邻的谱带序之间会有很大的间隔,而每一段中数据的递减的情况可以由式(6)的结论说明,随着υ″的增大,同一谱带序中的相邻两子带的波数间隔将逐渐减小,即同一谱带序的子带从下向上是按υ″增大的方向排列的。另外还发现,不但每一段中的数据是递减的,从下向上谱带序中各子带间的间隔也351到69逐渐变小了,式(6)中当Δυ从负值依次增大时,各子带的间隔将会始终减小。现在已经把数据按不同谱带序分开了。

由PN分子光谱图[10]可知,各个长波谱带序的第一个谱带具有υ′=0,因而形成了0的υ″前进带组;而各个短波谱带序的第一个谱带具有υ″=0,因而形成了0的υ′前进带组,由振动谱带前进带组的规律可知,向长波方向的υ″前进带组的谱带间隔随着υ″的增大而逐渐减小(由式(8)结论),向短波方向的υ′前进带组的谱带间隔随着υ′的增大而逐渐减小(式(11)的结论),中间存在着一个间距的突变,而间距突变的这个谱带序即是Δυ=0主谱带序。通过计算发现谱带序间的其中一个间隔(31643cm-1～29654cm-1)的数值最大,其值为1989cm-1,由此可以确定以波数29654cm-1开头的谱带序即为Δυ=0主谱带序。

表1 N2分子电子振动光谱波数、一次、二次差值及量子数跃迁Tabel 1 The wave number and the difference of the electronic vibration spectra of the N2 Molecularand transition between quantum numbers

3 N2分子电子振动光谱的德兰德斯表

3.1 德兰德斯表的绘制

把表1的数据按照光谱规律整理,就得到了N2分子电子振动光谱的德兰德斯表,如表2所示。表2中同一列谱线表示υ′前进带组;同一行谱线表示υ″前进带组。主对角线值对应于Δυ=0主谱带序,与它平行的对角线对应于Δυ=1、2等或Δυ=-1、-2 等谱带序。Δ01,Δ12,...,Δ56分别为υ′=0、1、2、3、4、5 的υ″列相邻谱带波数之差,即υ′=0、1、2、3、4、5 的υ″列谱带波数差Δσ(υ″)=σ(υ′→υ″)-σ(υ′→υ″+1),对应行的数值即为各差值的平均值;Δ10,Δ21,...,Δ43分别为υ″=0、1、2、3、4、5 的υ′列相邻谱带波数之差,即υ″=0、1、2、3、4、5 的υ′列谱带波数差Δσ(υ′)=σ(υ′+1 →υ″)-σ(υ′→υ″),对应列的数值即为各差值的平均值。

表2 N2分子电子振动光谱的德兰德斯表Tabel 2 The Deslandres table of the electronic vibration spectra of the N2 Molecular

3.2 德兰德斯表的分析

从式(8)中看出一次差值Δσ(υ″)与υ″成线性关系,由实验数据分别描绘出Δσ(υ″)随υ″的变化(图2),由得到的直线斜率给出~υe″χe″=1725.8cm-1,由截距得到~υe″=13.3cm-1。

同理,式(11)中Δσ(υ′)与υ′成线性关系 ,由实验数据分别描绘出Δσ(υ′)随υ′的变化(图 3),由得到的直线斜率给出~υe′χe″=1998.7cm-1,由截距得到~υe′=27.1cm-1。

图2 一次差值Δσ(υ″)与υ″的关系Fig.2 The relation of the first differenceΔσ(υ″)andυ″

图3 一次差值Δσ(υ″)与υ′的关系Fig.3 The relation of thefirst differenceΔσ(υ′)andυ′

4 结论

以N2分子电子光谱为例,基于对电子光谱的可见和紫外区域带系的粗结构分析,结合这些规律,对N2分子光谱的实验值进行了正确地指认,并形成了德兰德斯表,从而得到了N2分子低电子态的非谐性常数~υe″χe″和平衡振动频率~υe″,高电子态的非谐性常数~υe′χe′和平衡振动频率~υe′。

[1]夏慧荣,王祖庚.分子光谱学和激光光谱学导论[M].上海:华东师范大学出版社,1989:5-10.

[2]徐克尊.高等原子分子物理学(第2版)[M].北京:科学出版社,2006:172-184.

[3]朱正和,俞华根.分子结构与分子势能函数[M].北京:高等教育出版社,1997:97-105.

[4]马 靖,李 昂,李春燕.双原子分子振动光谱常数的拟合[J].安徽师范大学学报(自然科学版),2003,26(2),134-137.

[5]钟任斌,黄 整.N2分子振动的理论计算[J].贵州大学学报(自然科学版),2004,21(1):1-3.

[6]王国文.原子与分子光谱导论[M].北京:北京大学出版社,1985:199-202.

[7]赖 文.分子光谱学[M].徐广智,等.北京:高等教育出版社,185-189.

[8]胡士德,孙卫国,任维义,等.碱金属氢化物双原子分子部分电子态的完全振动能谱和分子离解能的精确研究[J].物理学报,2006,55(5):2185-2193.

[9]Herzberg G.Molecular Sprctra and Molecular StructureⅠ.Spectra of biaotomic molecules[M].New York:Van Nostrand Co,1950:151-158.

[10]G赫兹堡.分子光谱与分子结构(第1卷)[M].王鼎昌.北京:科学出版社,1983:24.

Electronic Vibration Structural Analysis of N2Molecular and the Drawing of Deslandres Table

ZHANG Yanwen,ZHANGJianjun
(Key Laboratory of Ecophysics,Department of Physics,Teacher's College,Shihezi University,Shihezi 832003,China)

Spectroscopy experiment was generally only the wavelength of spectral lines and the relative light intensity,how to identif y the wavelength of spectral lines which correspond to the transition f rom v’to v"and become a key of the next collation and data analysis.In this paper,diatomic molecules of the law of electronic vibrational spectra were analyzed,and in accordance with these laws correctly identified N2molecular vibration of the electronic spectral data,and finally sorted out the N2Vibrational Spectra of Molecular Electronics Deslandres table,through the Differential processing,eventually got the high state and low state of constant vibration about N2molecular spectroscopy.

N2molecular;electronic structure;spectrum;deslandres table

O562.3;O562.4

A

1007-7383(2010)01-0128-05

2009-09-07

张岩文(1979-),男,讲师,从事激光光谱研究;e-mail:zyw㊦tea@shzu.edu.cn。