非线性微分多项式分担一个非零拟公共值的亚纯函数的唯一性*
李效敏,胡海燕
(中国海洋大学数学科学学院,山东青岛266100)
非线性微分多项式分担一个非零拟公共值的亚纯函数的唯一性*
李效敏,胡海燕
(中国海洋大学数学科学学院,山东青岛266100)
本文利用A.Banejee与S.Mukherjee的方法证明了一类非线性微分多项式具有一个2阶拟公共值的亚纯函数的唯一性定理,改进了方彩云与方明亮,I.Lahiri与Mandal,以及A.Banerjee等人的有关结果。
亚纯函数;公共值;微分多项式;唯一性
0 引言及主要结果
本文中出现的亚纯函数是指复平面内的亚纯函数。文中采用Nevanlinna理论的标准符号[1-3]。本文中出现的E表示线性测度有穷的正实数集合,并且每次出现不必相同。对非常数的亚纯函数h,用T(r,h)表示h的Nevanlinna特征函数,S(r,h)表示满足S(r,h)=o{T(r,h)}(r→∞,r|E)的量。
设f与g是2个非常数的亚纯函数,a是1个有限值。如果f-a与g-a的零点相同,并且每个零点的重数也相同,则称f与g CM分担a。如果f-a与g-a的零点相同,并且不计零点的重数,则称f与g IM分担a。如果1/f与1/g CM分担0,则称f与g CM分担∞。如果1/f与1/g IM分担0,则称f与g IM分担∞。设m为正整数或无穷,b∈C∪{∞}。以下用Em)(b,f)表示f的重数≤m的b-值点的集合,并且每个b-值点考虑相应的重数。用(b,f)表示Em)(b,f)的精简形式。如果E∞)(b,f)=E∞)(b,g),则f与g CM分担b。如果(b,f)=(b,g),则f与g IM分担b[4]。
定义1[5]设p是正整数,a∈C∪{∞}。用Np)(r,1/(f-a))表示f的重数不大于p的a-值点的计数函数,这里每个a-值点考虑相应的重数;用(r,1/(f-a))表示相应的精简计数函数;用N(p(r,1/(fa))表示f的重数不小于p的a-值点的计数函数,这里每个a-值点考虑相应的重数;用(r,1/(f-a))表示相应的精简计数函数。
定义2[6]设f与g是2个非常数的亚纯函数,m为正整数,a∈C∪{∞}且Em)(a,f)=Em)(a,g)。设z是f的1个a-值点,重数为μ(z,a,f)。用(r,1/(fa))表示|z| 定义3[7]设f与g是2个非常数的亚纯函数,a∈C∪{∞}并且(a,f)=(a,g)。再设z∈C是f与g的1个公共a-值点,且重数为μ(z,a,f)。用NL(r,1/(f-a))表示|z| 1976年,杨重骏提出了下述问题。 问题1[8]如果2个非常数的整函数f与g CM分担0,f(n)和g(n)CM分担1,并且2δ(0,f)>1,这里n是1个非负整数,那么f与g将会有什么关系? 1990年,仪洪勋解决了问题1,证明了下述定理。定理1[9]设f与g是2个非常数的整函数。如果f与g CM分担0,f(n)与g(n)CM分担1,并且2δ(0,f)>1,这里n是1个非负整数,那么f(n)g(n)=1或f=g。 1997年,I.Lahiri提出了下述问题。 问题2[10]如果2个亚纯函数的非线性微分多项式CM分担1,将会有怎样的结果? 2001年,方明亮和魏宏回答了问题2,证明了下述结果。 定理2[11]设f与g是2个超越整函数,n≥11是1个整数。如果fn(f-1)f′和gn(g-1)g′CM分担1,那么f=g。 2002年,方彩云和方明亮改进了定理2,证明了下述定理。 定理3[12]设f与g是2个非常数的整函数,n≥9是1个整数。如果E2)(1,fn(f-1)2f′)=E2)(1,gn(g-1)2g′),那么f=g。 针对定理3,人们自然地提出下述问题。 问题3[6]如果定理3中的f与g是2个非常数的亚纯函数,将会出现什么结果? 2005年,I.Lahiri和N.M andal回答了问题3,证明了下述定理,从而改进了定理3。 定理4[13]设f与g是2个超越亚纯函数,并且,再设n≥17是1个整数。如果E2)(1,fn(f-1)2f′)=E2)(1,gn(g-1)2g′),那么f=g。 2007年,A.Banerjee改进了定理4并回答了问题3,证明了下述定理。 定理5[6]设f与g是2个非常数的亚纯函数,n是1个正整数,且满足,其中Θ(∞,f)+Θ(∞,g)>0。如果E2)(1,fn(f-1)2f′)=E2)(1,gn(g-1)2g′),那么f=g。 本文将改进定理5,证明下述结果。 定理6 设f与g是2个非常数的亚纯函数。如果E2)(1,fn(af2+bf+c)f′)=E2)(1,gn(ag2+bg+c)·g′),这里a≠0,b和c是复数并且|b|+|c|≠0,n是1个正整数,那么下述4种情形之一成立: (i)若b≠0,c=0,并且Θ(∞,f)+Θ(∞,g)>则f=g。 (ii)若b≠0,c≠0,并且az2+bz+c=0有2个不同的根,f和g中之一是只有重极点的非整函数的亚纯函数,则f=g。 (iii)若b≠0,c≠0,并且az2+bz+c=0有2个相同的根,则f=g。 (iv)若b=0和c≠0,则f=g或f=-g。若n是1个偶数,则f=-g不成立。 设F,G是2个非常数的亚纯函数,定义 设F和G IM分担1,以下用?N(1,1)(r,1/F)表示F-1和G-1的公共单零点的精简计数函数。 引理1[6]设F与G是2个非常数的亚纯函数,且满足E2)(1,F)=E2)(1,G),再设H由(1)式定义。如果H不恒等于0,那么,其中表示F与G在|z|<1内的重数相等且大于3的那些公共1-值点的精简计数函数。 引理2[6]设F与G是2个非常数的亚纯函数。如果E2)(1,F)=E2)(1,G),那么,其中N0(r,1/F′)表示是F′零点但不是F(F-1)的零点的计数函数,这里F′的每个零点考虑重数。 引理3[9]设f是1个非常数的亚纯函数,k是1个正整数。那么 引理4[14]设f是1个非常数的亚纯函数,再设这里an≠0,an-1,…,a1,a0是常数,那么T(r,P(f))= 引理5[15]设f与g是2个非常数的亚纯函数。那么 不恒等于α2,这里a,b,c是3个复数,且满足a≠0和是一个整数,α是不恒等于0,∞的亚纯函数,并且T(r,α)=S(r,f)。 引理6 设f与g是2个非常数的亚纯函数,再设 这里a,b,c是3个复数,且满足a≠0和|b|+|c|≠0,n>7是一个整数。如果 证明 由(2)可得 由引理4和(4)左边的等式可得 同理可证 由(5)和(6)可得 由引理4可得 同理可证 于是 以及 不失一般性,设存在1个集合IΑR+满足mes I=∞,使得 分以下3种情况讨论: 情形1 设B≠0,-1。如果A-B-1≠0,由(3)可得 由(4),(6),(13),引理2.3和第二基本定理可得 上式结合(7)-(13)可得 由此得n≤7,这与n>7矛盾。 如果A-B-1=0,则(3)可写为 由(14)可得 由(7),(11),(15)和第二基本定理可得T(r,G)≤ 上式结合(11),(12)可得 由此得n≤3,这与n>7矛盾。 情形2 设B=-1,则(3)可写为 若A+1≠0,由(16)可得 由(17),类似于情形1中的方法可得n≤3,这与n>7矛盾。 如果A+1=0,则(3)可写为FG=1,即 但由引理5和条件n>7可知,fn(af2+bf+c)f′·gn(ag2+bg+c)g′不恒等于1,这与(18)矛盾。 情形3 设B=0。那么(3)可写为 如果A≠1,由(19)可得 以下类似于情形1中的方法可得n≤7,这与n>7矛盾。 如果A=1,则(19)可写为F=G,从而得到引理6的结论。 引理7 设f与g是2个非常数的亚纯函数,F1和G1由(2)定义。如果n≥5,那么由=可得F1=G1。引理8[15]设F1和G1的定义如(2)式,n≥3是1个整数,如果F1=G1,那么以下4种情形之一成立:(i)若b≠0,c=0且,则f=g。 (ii)若b≠0,c≠0,az2+bz+c=0有2个不同的根,且f,g其中之一是只有重极点的非整函数的亚纯函数,则f=g。 (iii)若b≠0,c≠0,az2+bz+c=0有2个相同的根,则f=g。 (iv)若b=0,c≠0则f=g或f=-g。若n是1个偶数,则f=-g不成立。 设F和G的定义如(4)式,H的定义如(1)式。设H不恒等于0,则由引理1,引理2和引理3可得T(r,F)+T(r,G)≤ 其中ε是任意小正数。由(10),(11),(21)与引理3可得(n+1){T(r,f)+T(r,g)} 其中ε为任意充分小的正数。 由(22)可得 这与已知条件n>15-5m in{Θ(∞,f),Θ(∞,g)}矛盾。因此H≡0,由此可得(3)。于是引理6可得F′1=,这里F1与G1由(2)定义。再由引理7可得F1=。于是由引理8可得定理6的结论。定理6证毕。 [1] Hayman W K.Meromorphic Functions[M].Oxford:Clarendon Press,1964. [2] Laine I.Nevanlinna Theory and Comp lex Differential Equation[M].Berlin:Walter de Gruyter,1993. [3] Yang L.Value Distribution Theory[M].Berlin:Sp ringer-Verlag,1993. [4] Yang CC,Yi H X.Uniqueness Theory of Meromorphic Functions[M].Do rdrecht/Boston/London:Kluwer Academic Publishers,2003. [5] Alzahary T C,Yi H X.Weighted sharing three valuesand uniqueness of meromorphic functions[J].J Math Anal App l,2004,295(1):247-257. [6] Banejee A.A uniqueness result on some differential polynomials sharing 1-points[J].Hiroshima Math J,2007,37:397-408. [7] Yi H X.Meromorphic Functions that share one or two value[J].Comp lex Variables Theo ry App l,1995,28:1-11. [8] Yang C C.On two entire functions w hich together with their derivatives have the same zeros[J].J Math Anal Appl,1976,56:1-6. [9] Yi H X.Uniqueness of meromorphic functions and a question of C.C.Yang[J].Complex Var Theory Appl,1990,14:169-176. [10] Lahiri I.Uniqueness of meromorphic functions as governed by their differential polynomials[J].Yokohama Math J,1997,44:147-156. [11] Fang M L,Wei H.A unicity theorem for entire functions concerning differential polynomials[J].Indian J Pure App l M ath,2001,32:1342-1348. [12] Fang C Y,Fang M L.Uniqueness of meromorphic functions and differential polynomials[J].Comput Math Appl,2002,44:607-617. [13] Lahiri I,Mandal N.Uniquenessof nonlinear differential polynomials sharing simple and double 1-points[J].Int J Math Sci,2005,12:1933-1942. [14] Yang C C.On deficiencies of differential polynomialsⅡ[J].Math Z,1972,125:107-112. [15] Banejee A,M ukherjee S.Nonlinear differential polynomials sharing a small function[J].A rchivum Mathematicum(BRNO)Tomus,2008,44:41-56. On Uniqueness of Meromo rphic Functions Whose Nonlinear Differential Polynomials Have One Nonzero Pseudo Common Value L IXiao-M in,HU Hai-Yan By using the technique described by Banejee and M ukherjee,a theorem on uniquenessof meromorphic functions w hose nonlinear differential polynomials have one nonzero pseudo common value is p roved.This new result imp roves some p revious ones given by C.Y.Fang and M.L.Fang,I.Lahiri and M andal,A.Banerjee,and others. meromorphic functions;shared values;differential polynomials;uniqueness O174.52 A 1672-5174(2010)12-154-05 国家自然科学基金项目(10771121,40776006);国家自然科学基金中俄合作协定项目(10911120056);山东省自然科学基金项目 (Z2008A 01,ZR2009AM 008)资助 2009-07-14; 2010-02-03 李效敏(1967-),男,副教授。E-mail:xm li01267@gmail.com AMS Subject Classification: 30D30 责任编辑 朱宝象1 几个引理
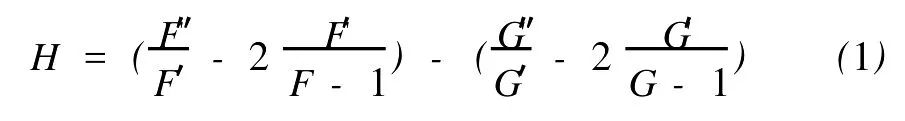
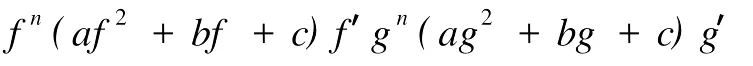
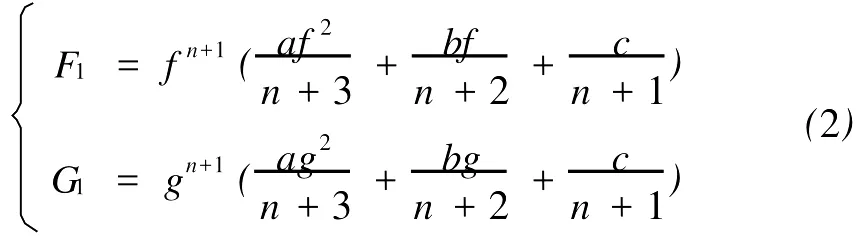
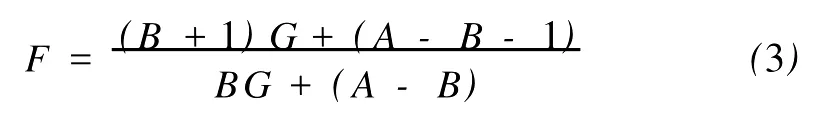
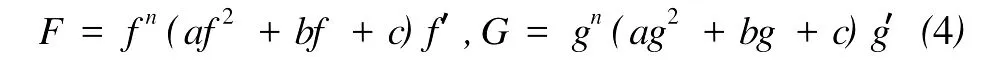
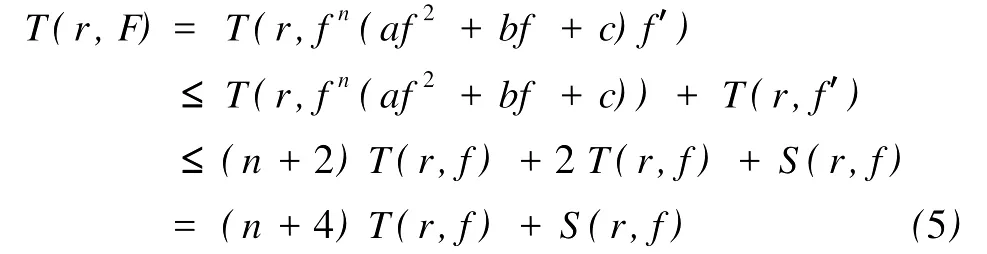
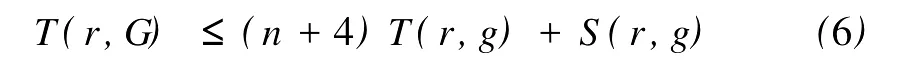
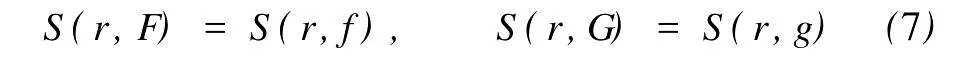
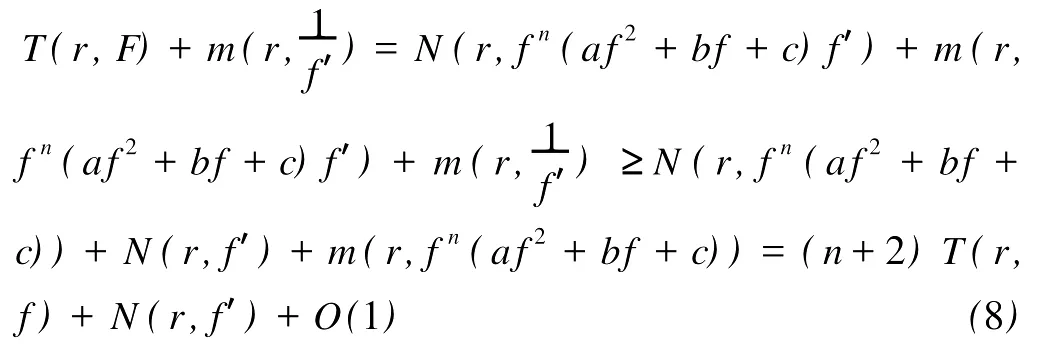
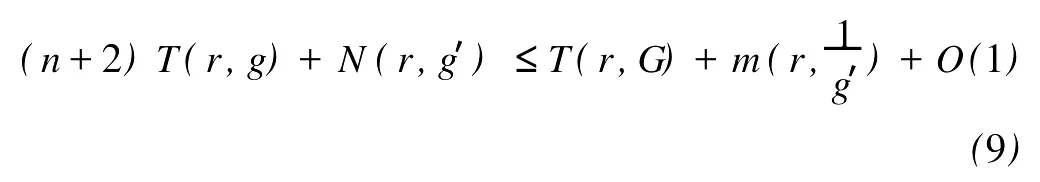
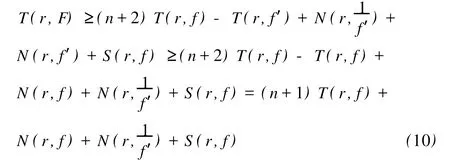
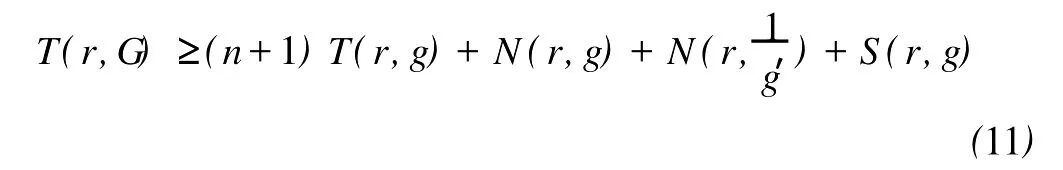
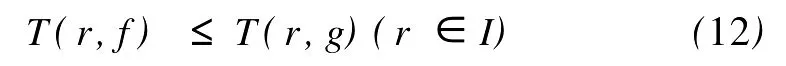
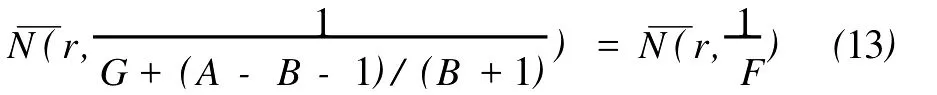
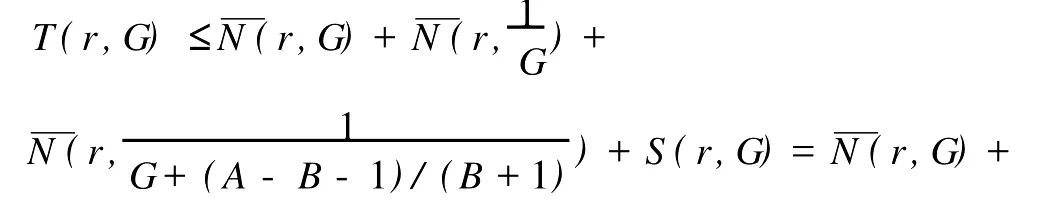
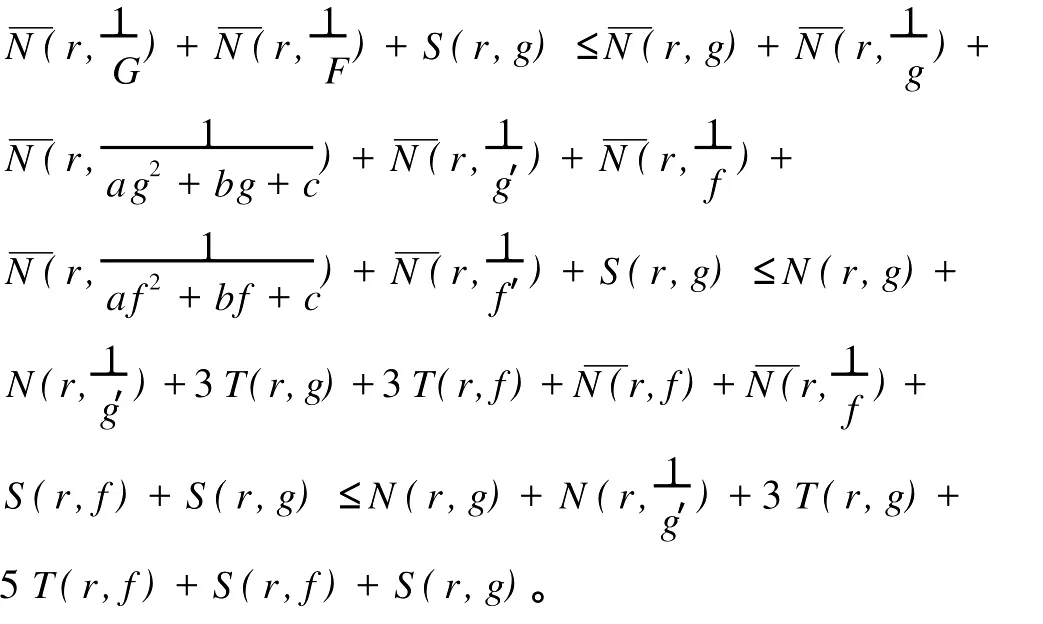
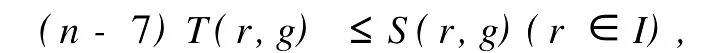
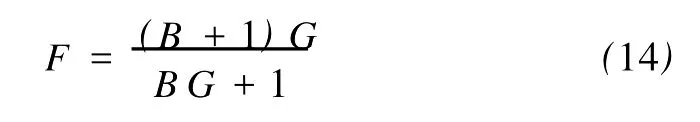
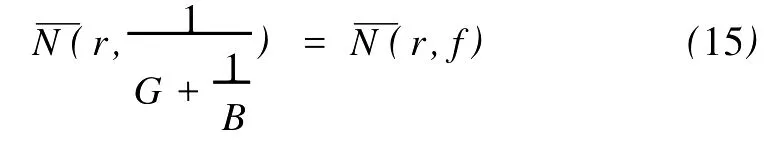
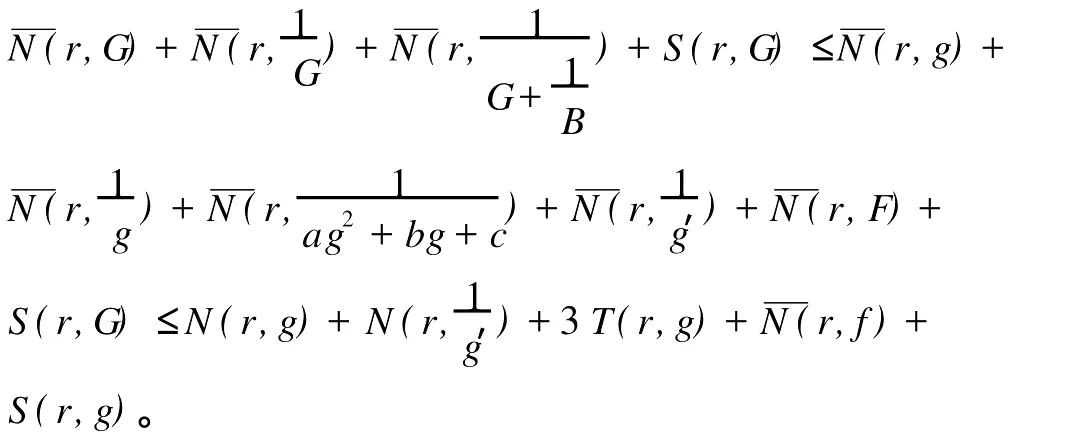
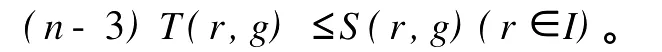
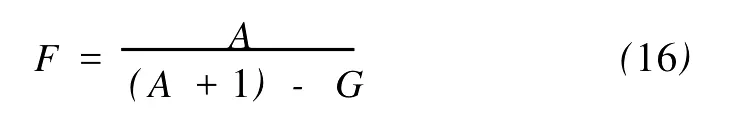
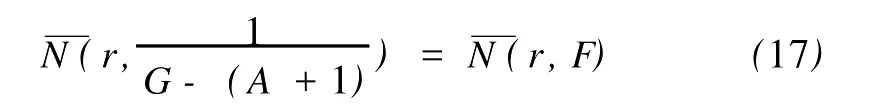
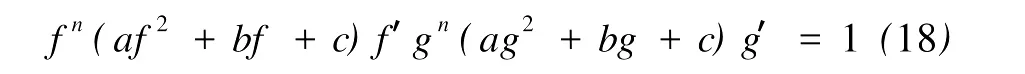
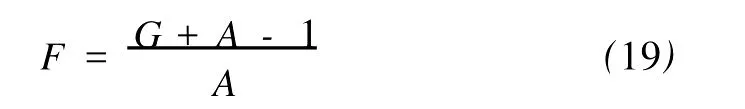
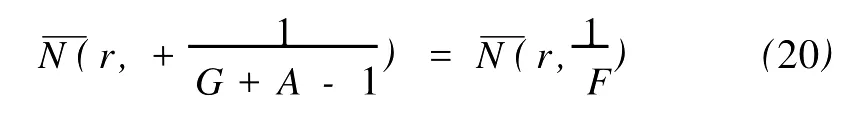
2 定理6的证明
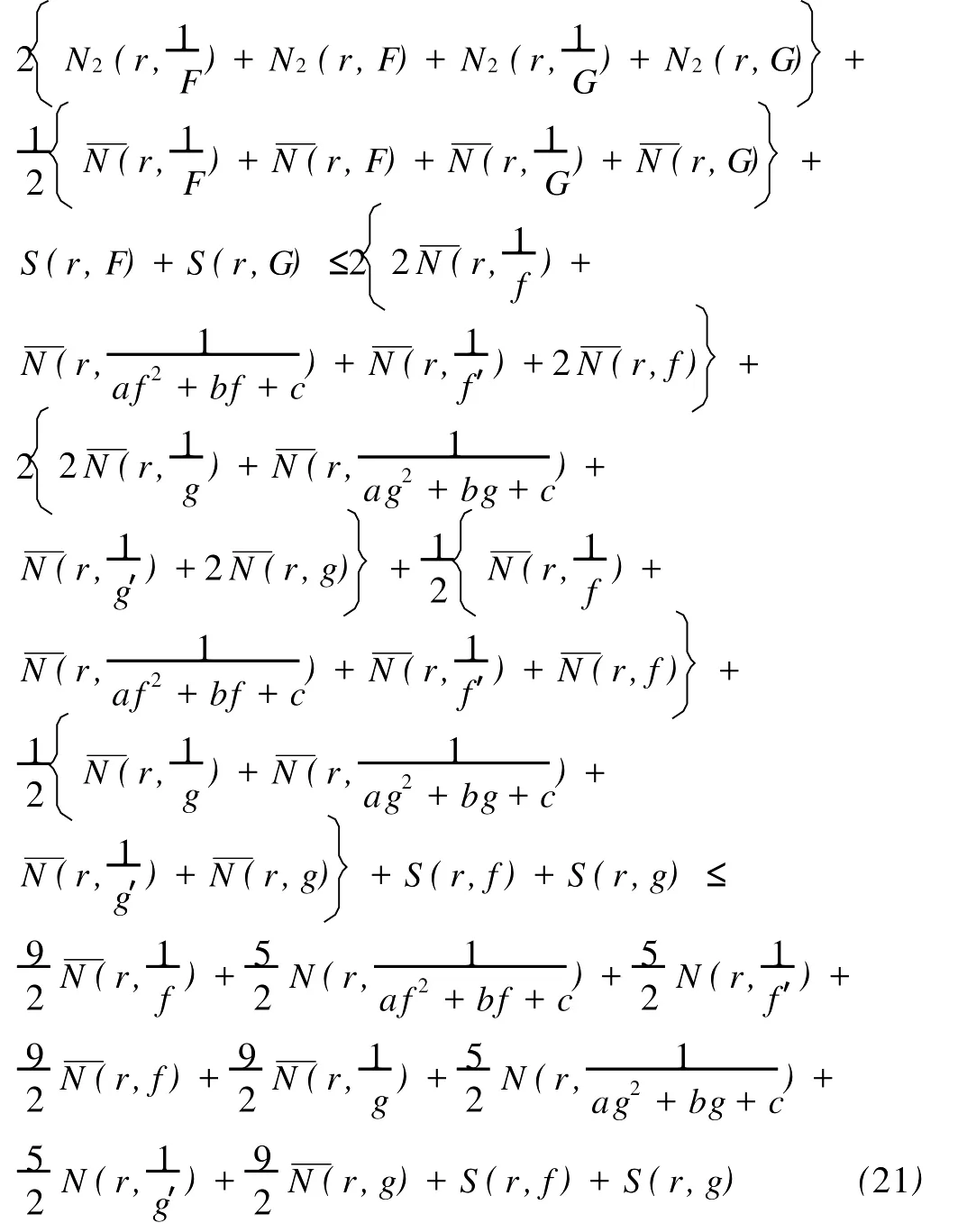
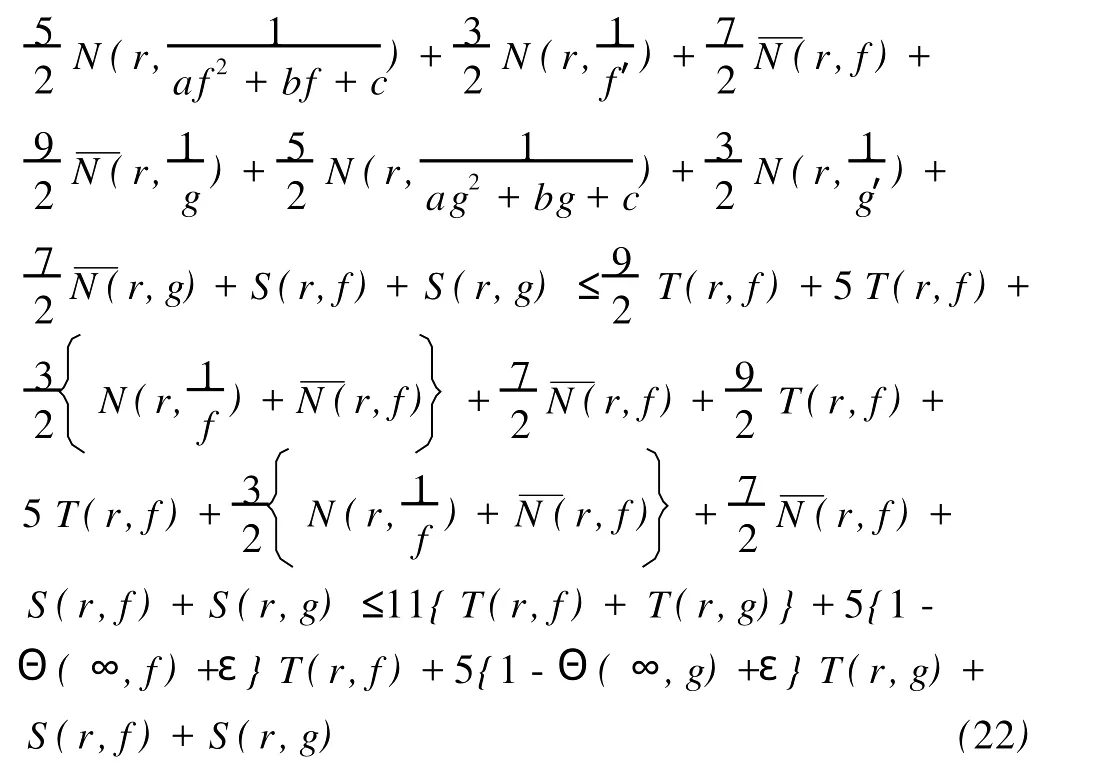
(School of Mathematical Sciences,Ocean University of China,Qingdao 266100,China)

