具有小延时反馈的逻辑生长过程中的稳态概率与极值分布

丁 川，韩立波 (长江大学物理科学与技术学院，湖北 荆州 434023)

具有小延时反馈的逻辑生长过程中的稳态概率与极值分布

丁 川，韩立波 (长江大学物理科学与技术学院，湖北 荆州 434023)

应用小延时近似方法，研究了关联高斯白噪声诱导的具有延时反馈的逻辑生长过程，得到了系统的稳态概率分布，分析了延时对稳态概率分布的影响，并对理论分析的结果进行了数值模拟比较。在参数空间中确定了稳态概率的极值区域，研究了延时对极值区域分布的影响。研究结果表明，延时反馈可以导致类相变现象的产生。

逻辑生长模型； 关联噪声； 延时反馈；稳态概率；极值

噪声对非线型系统的影响，是当前随机过程理论研究的重要课题。逻辑生长模型是一个典型的非线性系统，在生物学、遗传学、化学反应、人口动力学等学科领域中有广泛应用。特别地，逻辑生长模型可以对肿瘤细胞的生长过程进行很好的描述[1～3]。另外，由于物质、能量和信息的有限传播速度，延时反馈被引入到系统中[4]。近年来，Frank[5,6]提出了小延时近似的福克-普朗克描述方法，用以直接解决随机延时微分方程。笔者在小延时条件下，研究了被关联白噪声诱导的具有延时反馈的随机系统，并将其应用于具有延时的逻辑生长过程，对延时逻辑生长过程的稳态概率分布进行了理论分析和数值模拟。通过数值分析方法，确定了稳态概率分布的极值分布区域，并研究了延时对极值分布区域的影响。

1 模型及系统的稳态概率分布

关联噪声诱导的含有延时反馈的随机微分方程具有以下形式：

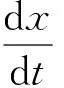
(1)

式中，f(x(t))为外场；x=x(t)，xτ=x(t-τ)分别表示在t时刻和t-τ时刻变量x的值；τ为时间延迟；g1(x(t))、g2(x(t))为噪声系数；ξ(t)和η(t)是高斯型白噪声，满足以下统计规律：

lt;ξ(t)gt;=lt;η(t)gt;=0 lt;ξ(t)ξ(t′)gt;=2Qδ(t-t′)

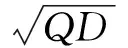
(2)

式中，Q和D分别是噪声ξ(t)和η(t)的强度；-1lt;λlt;1是ξ(t)和η(t)间的关联系数。

式(1)和式(2)可以转化为等效的随机微分方程：

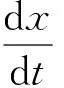
(3)

lt;Γ(t)Γ(t′)gt;=2δ(t-t′)

(4)

与式(3)等效的Ito形式[2]为：

dx(t)=F(x(t),x(t-τ))dt+G(x(t))dW(t)

(5)

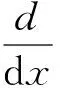
应用小延时近似，式(5)可以转化为：

dx=Fa(x)dt+Ga(x)dW

(6)

(7)

由式(6)可以得到变量x的稳态概率分布：

(8)

式中，N为归一化常数。

具有延时反馈的逻辑生长过程的随机微分方程[4,5]满足：

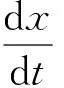
(9)

其中，a和b为大于0的系数。

对比式(1)和式(9)有：

f(x,xτ)=[a-bxτ]xg1(x)=xg2(x)=1

由式(4)和式(7)，可以得到：

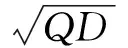
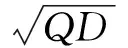
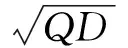
与式(9)相应的近似稳态概率分布为：

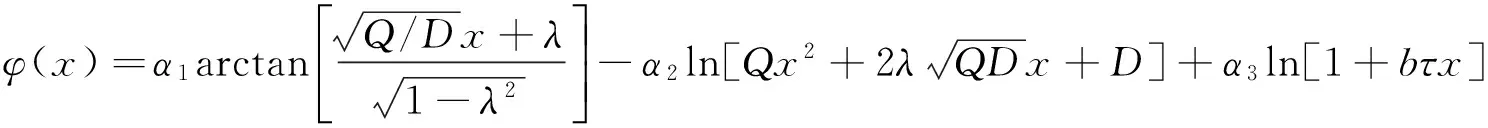
稳态概率分布Pst(x)的极值由方程：

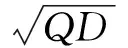
决定。极值点位于：

极值的数目由：

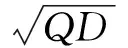
决定。在λlt;0区域内，稳态概率分布仅存在单一极值，该极值为极大值；在λgt;0区域内，当Δ=0时，稳态分布具有单极值，Δgt;0时，分布具有双极值，一个极大和一个极小，Δlt;0时，分布无极值情况。

2 延时反馈对稳态概率分布和极值区的影响

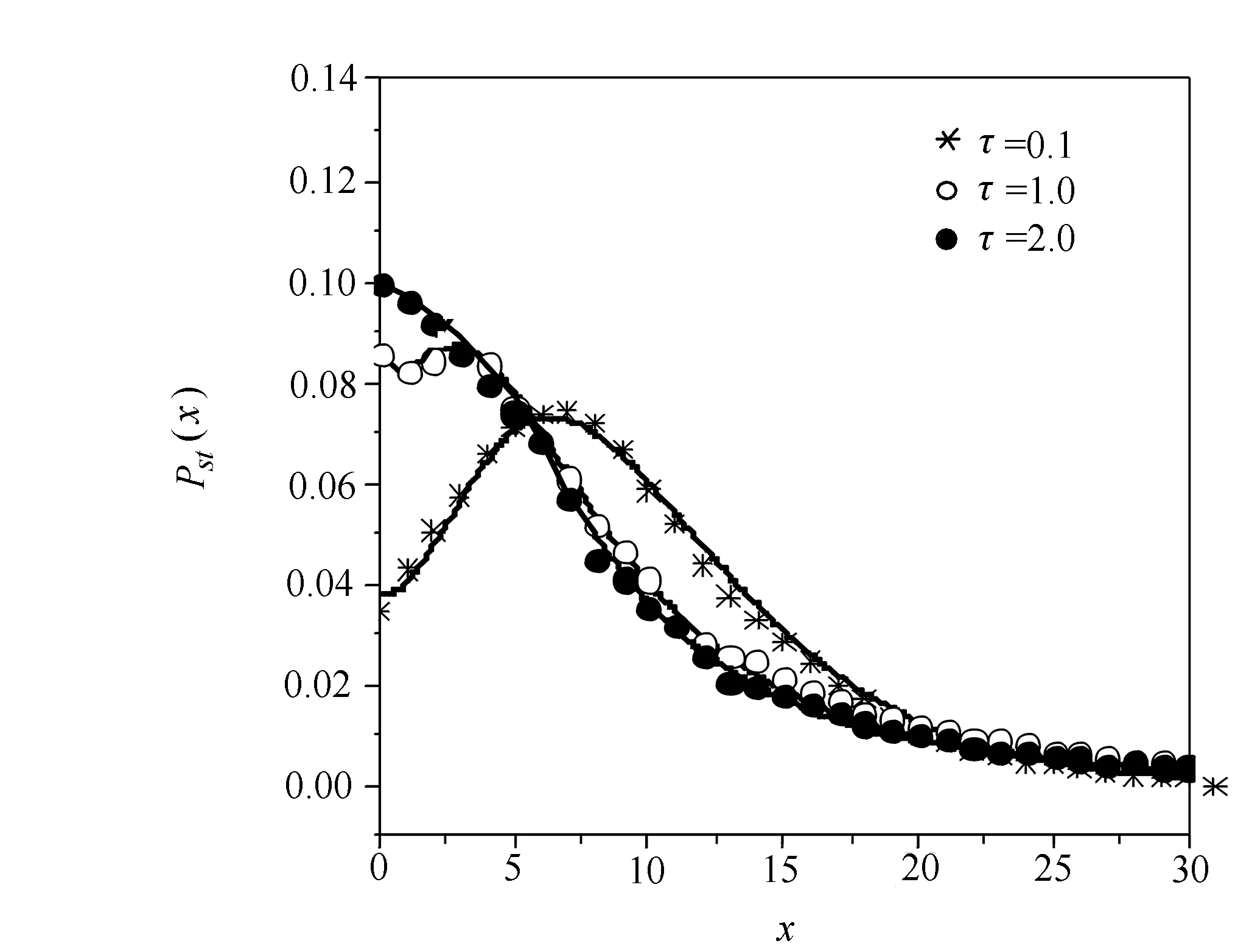
图1 不同延时条件下稳态概率分布Pst(x)随x的变化关系曲线

在不同延时条件下，稳态概率分布随变量x的变化关系曲线由图1所示，图1中同时给出了相应的数值模拟。由图可知，在给定的参数条件下，当τ=0.1时，曲线存在一个明显的极大值，极小值几乎靠近x=0。当τ增加到τ=1.0时，峰和谷的位置相互靠近，显示出明显的双极值结构特征。当τ增加到τ=2.0时，极大值和极小值均消失，曲线成为单调变化。图中还显示，在小延时条件下，数值模拟与解析分析的结果完全符合。

应用数值计算技术，稳态概率分布在参数空间(Q-λ)和(Q-D)中的极值分布区域绘于图2。区域符号“T”表示该区域具有2个极值，“N”表示该区域不存在极值。曲线为区域的分界线，即由无极值结构向双极值结构发生转化的转化线。由图2(a)可知，在Q-λ空间中，随着延时τ增加，分界线整体向下移动，双极值区域减小。由图2(b)可知，分界线向左移动，曲线斜率出现明显变化。

根据以上分析可知，在由关联高斯型白噪声诱导的延时逻辑生长过程中，系统的稳态概率分布会受到延时反馈的影响，当延时 发生改变时，系统的稳态概率分布曲线的结构可以发生转换，即从无极值结构变化到双极值结构，这表明，延时反馈也可以导致类相变现象的产生。

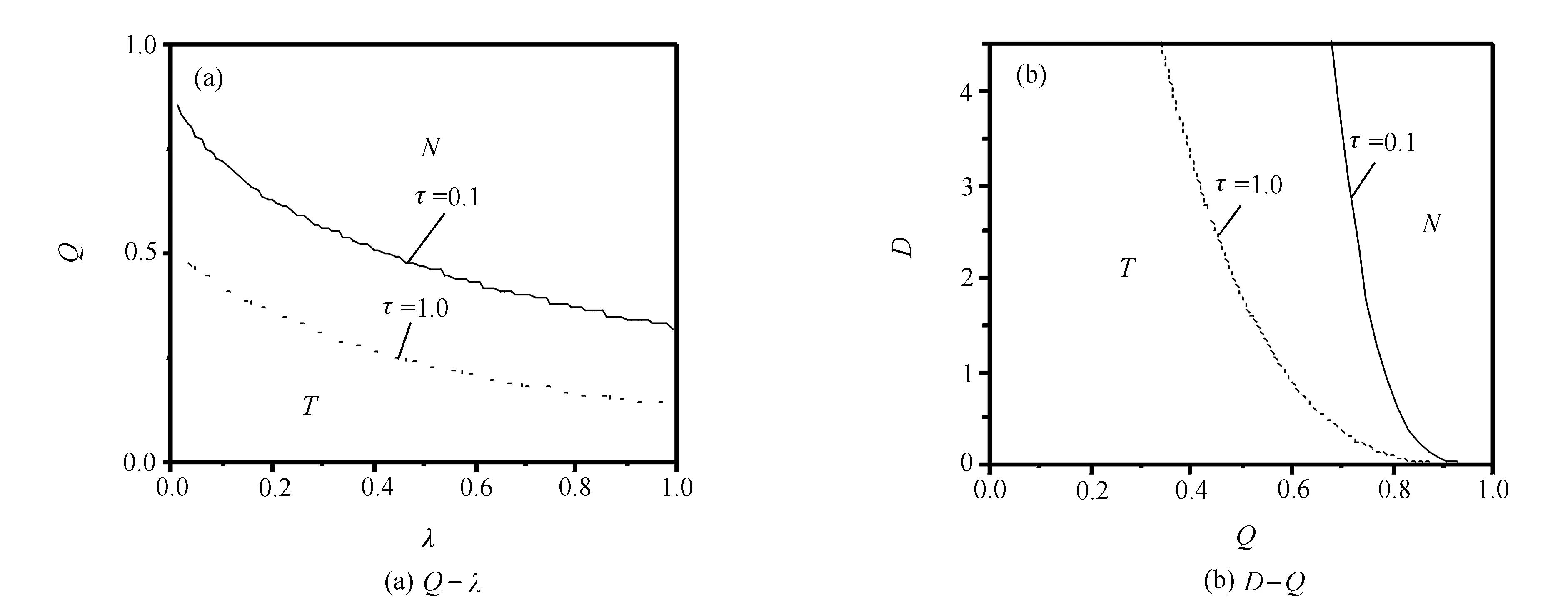
图2 稳态概率分布在参数空间中的极值分布区

[1]Ai Bao-Quan, Wang Xian-Ju, Liu Gao-Tao,etal.Correlated noise in a logistic model[J].Phys Rev E, 2003，67:022903-1～022903-3.

[2]韩立波.延时对色关联噪声诱导的逻辑生长过程的影响[J].物理学报，2008, 57(5)： 2699～2703.

[3]别梦杰，钟伟荣，陈弟虎，等.关联白噪声对抗肿瘤体系免疫效果的影响[J].物理学报，2009，58(1) ：97～100.

[4]Wu Dan, Zhu Shi-qun. Stochansetic resonance in a bistable system with time-delayed feedback and non-Gaussian noise[J].Phys Lett A, 2007，363： 202～212.

[5]Frank T D.Delay Fokker-Planck equations, Novikov,s theorem, and Boltzmann distributions as small delay approximations[J].Phys Rev E, 2005，72：011112-1～011112-9.

[6]Frank T D.Delay Fokker-Planck equations,perturbation theory, and data analysis for nonlinear stochastic systems with time delay[J].Phys Rev E, 2005，71： 031106-1～031106-14.

[编辑] 洪云飞

O415.6

A

1673-1409(2009)02-N026-03

2009-02-19

湖北省教育厅重大项目(Z200612001)。

丁川(1982-)，男，2004年大学毕业，硕士生，现主要从事理论物理方面的研究工作。