22面体平图的顶点4着色研究

侴万禧，黄云峰 (安徽理工大学土木建筑学院，安徽 淮南 232001)

李晓毅 (沈阳师范大学数学与系统科学学院，辽宁 沈阳 110034)

22面体平图的顶点4着色研究

侴万禧，黄云峰 (安徽理工大学土木建筑学院，安徽 淮南 232001)

李晓毅 (沈阳师范大学数学与系统科学学院，辽宁 沈阳 110034)

阐明了对偶图G(p,q,f)的4着色的基本思路，给出了对偶树的定义，提出了依据对偶图G(p,q,f)的2棵对偶树TA及TB的分解，实现对偶图G(p,q,f)的4着色的方法，最后介绍了22面体平图的顶点4着色的全过程，并分析了对偶树TA、TB的性质。

对偶图；对偶树；4着色；连通分支

1 基本思路

定义1[1,2]设任意平图的对偶图为含p个顶，q个边和f个面的平图，记为G(p,q,f)，则对偶图G(p,q,f)的p-2个边所导出的2个不含圈的可2着色的连通分支TA和TB称为对偶树。

对偶树TA的(p-3)/2或(p-5)/2个边与G(p,q,f)中f个面相关联，对偶树TB的(p-1)/2或(p+1)/2个边与G(p,q,f)中f个面相关联。

借助对偶图G(p,q,f)的2棵对偶树TA及TB的分解，可以实现对偶图G(p,q,f)的4着色，这是因为对偶树TA的2着色和对偶树TB的2着色等价于对偶图G(p,q,f)的4着色。

命题1[3,4]设平图的对偶图为G(p,q,f)，而对偶图G(p,q,f)的对偶图为G′(f,q,p)，则对偶图G(p,q,f)的2棵对偶树TA和TB与对偶图为G′(f,q,p)的H路径p是相互依存的(如图1)。

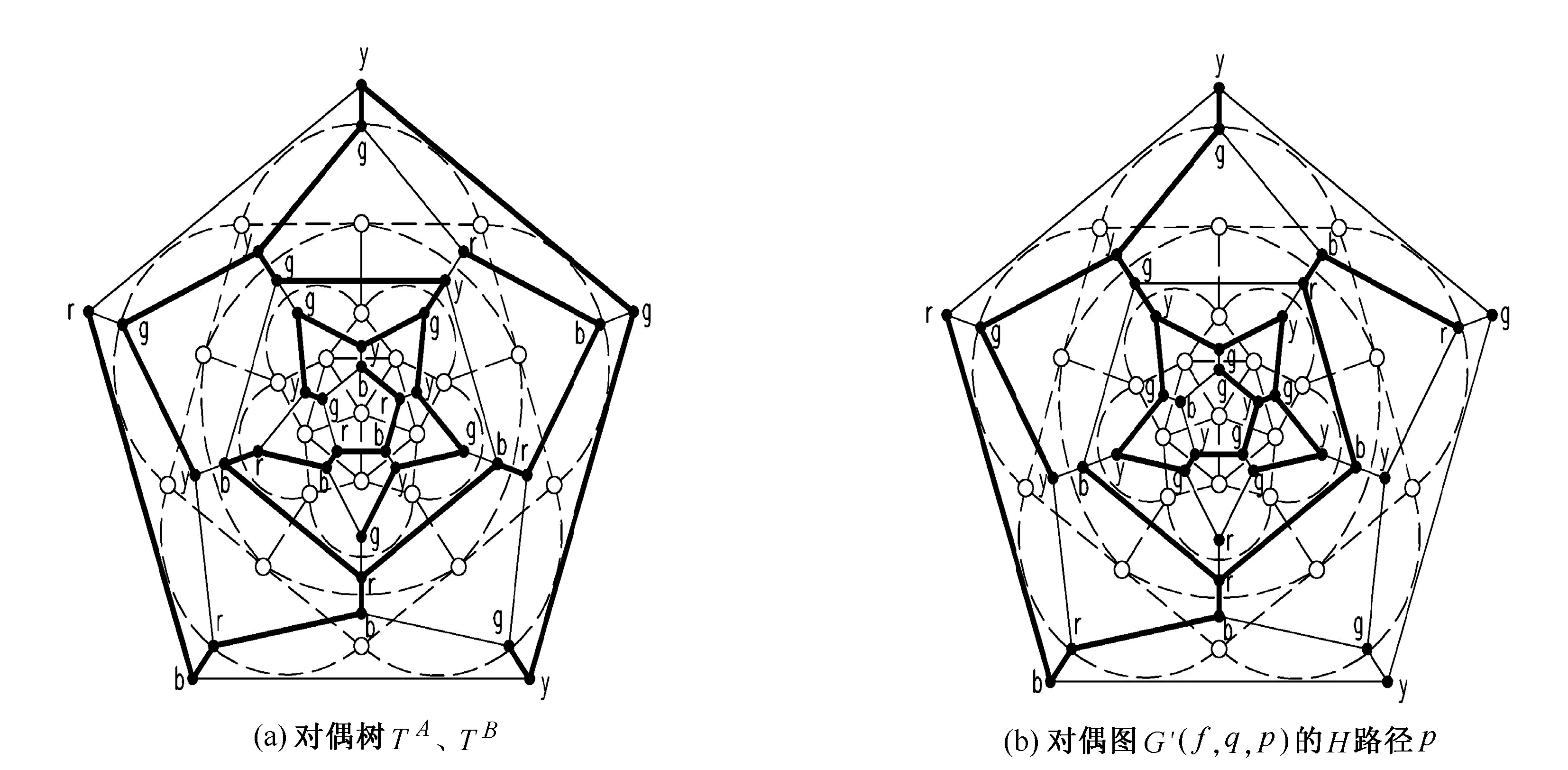
图1 对偶树TA、TB与对偶图G′(f,q,p)的H路径p

由图1可得，基于命题1的对偶树的一个算法：依据H路径求对偶树TA及TB。反之，倘若对偶树TA及TB依据它们自身的性质被确定，则对偶树TA及TB就自然的将G(p,q,f)的f个面分隔出一条通过f个相邻面中心的畅通路——H路径p，H路径p成为对偶树TA及TB正确与否的标志。

2 对偶图G(p,q,f)的4着色方法

设对偶图G(p,q,f)为p=35,q=55,f=22的平图，对偶图G(p,q,f)的对偶图G′(f,q,p)为f=21,q=55,p=35的平图，则对偶图G(p,q,f)的4着色的步骤如下：

1)将含f个顶，q个边和p个面的对偶图G′(f,q,p)分解出1条通过f个面中心的H路径p(如图2)。

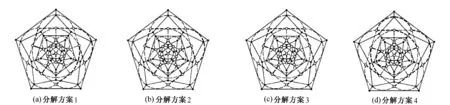
图2 对偶图G′(f,q,p)的H路径p的分解

2)让G(p,q,f)中的与H路径未交的p-2=33个边构成2棵对偶树TA及TB，使得TA由(p-5)/2=15或(p-3)/2=16个边构成，而TB由(p-1)/2=17或(p+1)/2=18个边构成(如图3)。

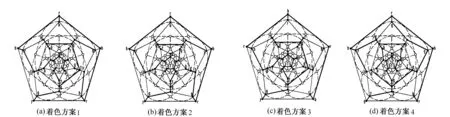
图3 对偶图G(p,q,f)的4着色

3)用y,g为对偶树TA着色，用r,b为对偶树TB着色，使得TA的2着色和TB的2着色等价于G(p,q,f)的4着色，即有：

∂(TA)+∂(TB)=∂(G)

3 对偶树TA及TB的性质

22面体平图G(p,q,f)所分解出的2棵对偶树TA及TB具有下列性质：

1)对偶树TA的(p-3)/2=16或(p-5)/2=15个边与G(p,q,f)的f=22个面相关联，对偶树TB的(p-1)/2=17或(p+1)/2=18个边也与G(p,q,f)的f=21个面相关联。

2)对偶图G(p,q,f)的每个面为对偶树TA及TB的构造贡献出3个边。

3)对偶树TA的边总是试图包围对偶树TB的边，而对偶树TB的边也总是试图包围对偶树TA的边。

4)对偶树TA和对偶树TB将对偶图G(p,q,f)的f-1=21个面分隔成一条畅通道，亦即形成一条通过f-1=21个面中心的H路径p。

5)对偶树TA和对偶树TB是G(p,q,f)中的与H路径p未交的p-2=33个边构成的。

[1]Beineke L W, Wilson R J.Selected Topics in Graph Theory[M]. London: Academic Press，1978.

[2]Bollobas B.Extramal Graph Theory[M]. London:Academic Press，1978.

[3]Douglas B.West Introduction to Graph Theory[M].Beijing: China Machine Press， 2004.

[4]徐俊明.图论及其应用[M].合肥：中国科学技术大学出版社，2004.

[编辑] 洪云飞

O157.5

A

1673-1409(2009)02-N014-02

2009-03-10

国家自然科学基金资助项目(10471096)。

侴万禧(1930-)，男，1956年大学毕业，教授，现主要从事岩石力学及图论方面研究工作。