低比转速泵圆柱形叶片型线的研究

汪建华 蒋文书

(长江大学机械工程学院，湖北 荆州 434023)(上饶职业技术学院，江西 上饶 334109)

低比转速泵圆柱形叶片型线的研究

汪建华 蒋文书

(长江大学机械工程学院，湖北 荆州 434023)(上饶职业技术学院，江西 上饶 334109)

根据叶片进出口边界条件，提出用三次多项式构造叶片型线的极坐标表达式，并导出了保证叶片安放角单调变化的叶片包角取值范围。该叶片型线的主要特点是其包角可作为设计常量由设计人员根据需要事先在一定范围内给定，并且随着叶片半径的增大，叶片曲率半径单调增长，叶片安放角单调均匀变化，从而减少了叶片表面的脱流损失，提高了离心泵的水力效率。

离心泵；叶轮；圆柱形叶片；叶片型线

低比转速离心泵叶轮叶片大多采用圆柱形叶片，圆柱形叶片工作面或背面的轮廊线即为叶片型线。离心泵叶轮叶片型线设计，直接影响水泵的性能。因此，一直受到设计人员的重视。叶片型线分为单圆弧叶片、双圆弧叶片、渐开线、等角螺旋线、等变角螺旋线、非等变角螺旋线等[1]。除了非等变角螺旋线外，这些叶片型线的包角是由叶片进出口边界条件决定的定值，即设计人员不能根据泵的比转速和叶片数的大小选取叶片包角，这是导致一些低比转速叶轮水力性能不高的主要原因。为此，文献[2]基于艾尔米特插值方法导出了可控包角圆柱形叶片型线方程，其叶片包角可由设计人员根据需要给定。笔者根据叶片型线进、出口4个边界条件，提出用三次多项式构造叶片型线的极坐标表达式，该表达式虽本质上与文献[2]完全相同，但推导方法和表达形式更简单；笔者还从理论上证明任何圆柱形叶片若叶片安放角从叶片进口单调变化到出口，中间不出现极值，则其叶片包角应在一定范围内选取；探讨了叶片包角对叶片型线形状的影响。

1 叶片型线的三次多项式表达式

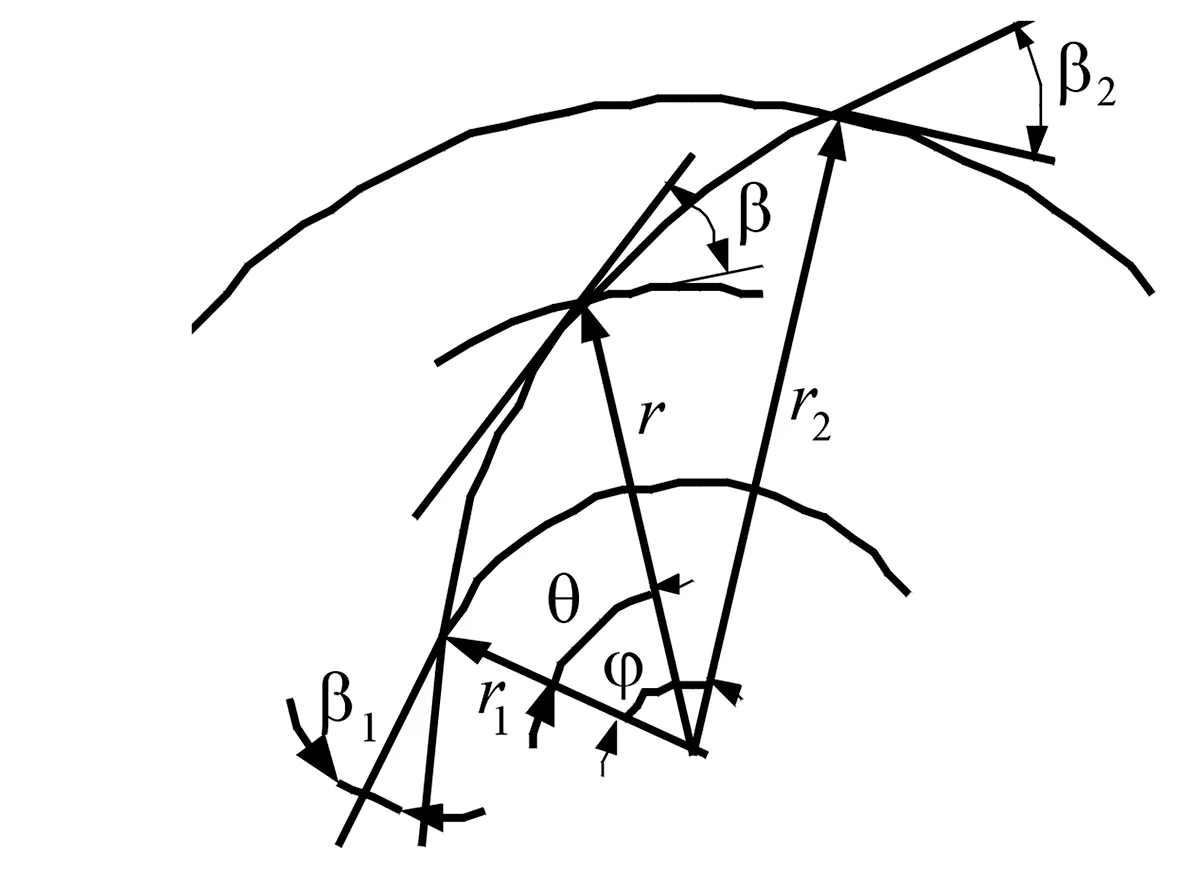
图1 圆柱形叶片型线图

如图1所示，叶轮叶片型线上任意点的半径为r、叶片安放角为β、叶片角为θ，叶片型线进出口半径和安放角分别为r1、r2和β1、β2，叶片包角为φ。

由于叶片型线进、出口边界条件有4个，即当θ=0时，r=r1，β=β1；当θ=φ时，r=r2，β=β2，故可用三次多项式构造叶片型线。即:

r=a0+a1θ+a2θ2+a3θ3

(1)

式中，a0、a1、a2、a3为由叶片进、出口边界条件确定的待定系数。

根据微分几何，叶片型线上任意点的叶片安放角β[3]:

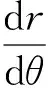
(2)

将式(2)代入式(1)得:

a1+2a2θ+3a3θ2=rtanβ

(3)

将叶片型线进、出口4个边界条件相应代入式(1)和式(3)求得系数a0、a1、a2、a3，并将a0、a1、a2、a3的值代入式(1)，得到的叶片型线数学表达式为:

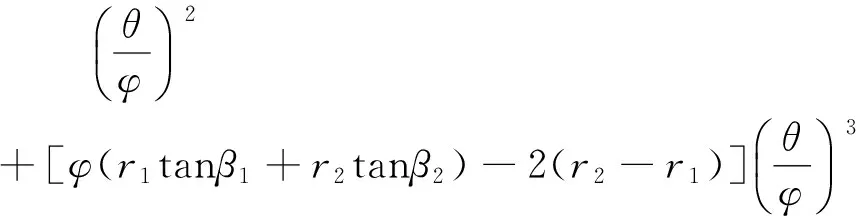
(4)

由此还可得到:

(5)

将式(4)和式(5)代入式(2)可得到叶片安放角:

(6)

2 三次多项式表示的叶片型线包角的取值范围

为保证圆柱形叶片型线有良好的水力特性，叶片安放角β应从叶片入口处的β1单调变化到出口处的β2，中间不应出现极值。下面分别讨论β1lt;β2或β1gt;β22种情况下叶片包角φ的取值范围。

同理，当β1gt;β2时、若叶片安放角β从叶片入口处的β1单调递减到出口处的β2，有:

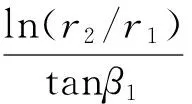
(8)

综合上述2种情况，对任何圆柱形叶片型线而言，若叶片安放角β单调变化，则叶片包角φ的取值范围应介于ln(r2/r1)/tanβ1与ln(r2/r1)/tanβ2之间。若φ不在上述范围内取值，则叶片安放角β一定是具有极大值或极小值的连续函数，这会导致低比速叶轮叶片流道之间发生脱流。在β1与β2相差较大的的情况下，叶片包角φ的选取范围较大；反之，叶片包角φ的选取范围较小。

叶片包角φ在ln(r2/r1)/tanβ1与ln(r2/r1)/tanβ2之间取值，只是保证叶片安放角β单调变化的必要条件。实际上若要叶片安放角β单调变化，三次多项式表示的叶片型线其包角φ的取值范围比式(7)或式(8)要略小。

3 叶片包角对叶片型线形状的影响

由三次多项式表示的叶片型线可知，当叶片进出口参数r1、r2、β1和β2给定后，叶片型线形状随叶片包角变化而变化。

当β1=β2时，叶片包角φ为定值ln(r2/r1)/tanβ1，计算表明式(4)表示的叶片型线非常接近螺旋线，即叶片型线为r=r1exp(θtanβ1)。

4 曲率半径

为了抵制叶片表面脱流，减少低比转速离心泵叶轮内的水力损失，不仅叶片安放角应单调变化，且叶片型线上各点曲率半径从进口到出口应单调上升。平面直角坐标系下曲线y=y(x)的曲率半径ρ为:

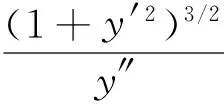
(9)

设曲线y=y(x)的极坐标方程为r=r(θ)，即x=rcosθ，y=rsinθ，则曲线y=y(x)的一阶导数和二阶导数分别为:

(10)

(11)

将式(10)、式(11)分别代入式(9)即得到极坐标系下的曲率半径表达式:

(12)

5 算 例

图2 不同包角下的圆柱形叶片平面投影

某离心泵叶轮叶片进出口半径和安放角分别为r1=20mm、r2=50mm和β1=30°、β2=20°。由式(8)得，叶片安放角β单调变化时的包角φ最大取值范围应介于φmin=80.5°与φmax=127.5°之间。

图2为叶片包角φ=85°、φ=95°、φ=105°和φ=120°时由式(4)计算得到的叶片平面投影图。

图3为叶片安放角β随叶片角θ变化图，当叶片包角φ靠近φmin和φmax的边缘选取时，叶片安放角β是一定是具有极大值或极小值的连续函数。为了保证β调变化，式(4)表示的叶片型线其叶片包角φ的取值范围比式(7)或式(8)的计算值小。

图4为叶片型线的曲率半径ρ随叶片半径r的变化图，除了φ=85°，其它叶片型线从进口到出口的曲率半径随叶片半径r逐渐增大，有利于克服叶片表面脱流，改善低比速离心泵叶轮的水力性能。

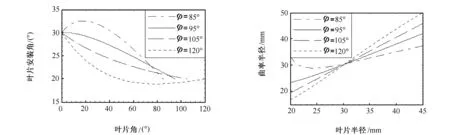
图3 叶片安放角变化图 图4 叶片型线曲率变化图

6 结 论

1)笔者给出的用三次多项式表示的圆柱形叶片型线，其叶片包角可作为设计常量由设计人员根据需要事先给定，避免了传统的各类圆柱形叶片其包角不可调控的缺陷。

2)圆柱形叶片型线的叶片安放角从叶片进口到叶片出口单调变化的必要条件为叶片包角取值范围介于ln(r2/r1)/tanβ1与ln(r2/r1)/tanβ2之间。

3)用三次多项式表示的叶片型线其包角在一定范围内选取时，叶片型线具有随着叶片半径增大，叶片曲率半径单调增长，叶片安放角单调均匀变化的特性，这有利于减少圆柱形叶片表面的脱流损失，提高离心泵的水力效率。

[1]董志豪,钱正峰.三种圆柱形叶片型线方程比较[J].排灌机械, 1998, 16(1): 16～18，31.

[2]严敬.离心泵可控包角圆柱形叶片型线方程[J].排灌机械,2008,26(5) :46～49.

[3]陈乃祥,吴玉林.离心泵[M].北京:机械工业出版社,2003.118～119.

[编辑] 易国华

TH311

A

1673-1409(2009)03-N085-03

2009-06-01

湖北省教育厅2009年度高校产学研合作资助项目(CXY2009A007)。

汪建华(1964-)，男，1985年大学毕业，硕士，副教授，现主要从事机械设计及流体机械方面的教学与研究工作。