基于常规测井曲线频谱分析的多尺度地质分层

易觉非

(长江大学信息与数学学院，湖北 荆州 434023)

基于常规测井曲线频谱分析的多尺度地质分层

易觉非

(长江大学信息与数学学院，湖北 荆州 434023)

测井曲线的频谱具有其特殊的地质意义，即测井曲线的不同频率与不同尺度地层相对应。首先讨论了测井曲线频率与地层的关系，进一步给出了用带通滤波进行多尺度地质分层的方法，最后，通过一个实际分层实例，说明了方法的正确性和有效性。

测井曲线;频谱;带通滤波

在信号分析中，有时域分析方法和频域分析方法2类，有些信号特征在时域中难以获得，在频域中则容易获得，反之亦然。因此，时域分析方法和频域分析方法两者缺一不可，互为补充。测井曲线的分析也不例外，可以在深度域(即时域)中，分析其依深度变化的规律，当将它转换到频域时，则可以分析其结构特征，发现其频率对应的地质意义。比如用频谱分析方法来确定沉积旋回和层序地层[1,2]。在利用测井资料进行地质分层方面，笔者在文献[3]中详细阐述了活度分层法的原理和算法，该方法能够快速有效的确定地层界面，但不能反映地层的尺度变化规律。下面，笔者从频谱分析的基本原理出发，结合测井曲线的频谱特征及其地质意义，给出了利用测井曲线频谱进行多尺度地质分层的方法。

1 基本原理

常规测井曲线是一系列不同厚度地层的数字化，因此，可将它理解为一系列宽度不同的矩形脉冲的叠加，图1为塔里木盆地哈得地区某井的自然伽玛曲线，体现了这一解释的合理性。

图1 近似矩形脉冲的自然伽玛曲线

依据矩形脉冲及其频谱响应，地层与常规测井曲线的频谱应具有如下关系：

1)厚地层谱幅高，频率衰减快，薄地层则相反；

2)频率与层厚成反比例关系，厚地层频率低，薄地层则相反。

因此，可以认为不同厚度地层对应不同频率范围，一般来说，较厚地层占据低频段，较薄地层占据高频段。依据这一原理，笔者提出了采用测井曲线带通滤波进行多尺度地质分层的方法。

2 主要算法

实现测井曲线多尺度地质分层的主要算法流程如图2所示。

图2 算法主要流程

1)傅里叶变换 输入为常规测井曲线，输出为常规测井曲线的频谱，可采用基2快速傅里叶变换(FFT:Fast Fourier Transform)算法[4]。

2)带通滤波 输入为测井曲线频谱，输出为经过滤波器滤波后的测井曲线频谱。这一步是实现分层的关键，滤波器设计[5]不合理，则不能体现地层特征，影响分层结果。主要从以下2个方面考虑滤波器的设计：滤波器的频带范围[flow,fhigh]。在此引入空间频率的概念，物理意义为单位深度内常规测井曲线波形变化次数，单位为次/m，记为1/m。其中，flow为低截频；fhigh为高截频，该频带既不能太宽(以防止不同层级的地层频率相互混淆),又不能太窄(以防止同一尺度地层频率遗漏)。②[flow,fhigh]之间的优势频率fext。它是同尺度地层的主要频率。

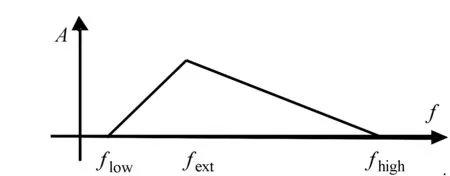
图3 三角形带通滤波器

3)傅里叶反变换 输入为经过滤波器滤波后的测井曲线频谱，输出为滤波后的测井曲线。

4)确定地层界面 输入为滤波后的测井曲线，输出为地层界面点。地层界面点可以采用活度分层法[3]计算。

5)分层结束 分层结束条件设定为测井曲线的截止频率fmax，若深度采样间隔τ=0.125m，截至频率可设为fmax=4(1/m)。如果滤波器频带范围[flow,fhigh]中fhighlt;fmax，则重复2)、3)、4)步，最终得到不同尺度的地层界面。

3 分层实例

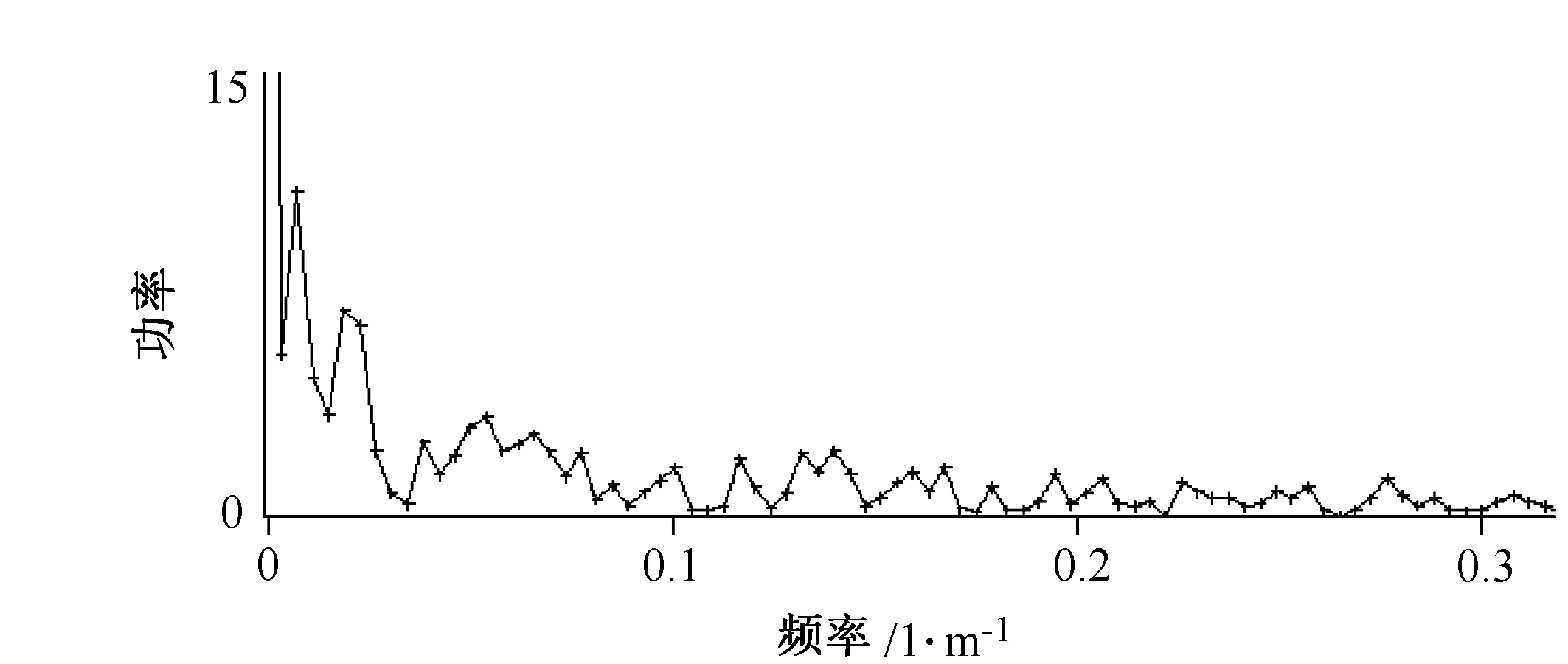
图4 某井自然伽玛曲线频谱

常规测井曲线中，自然伽玛曲线最能反映泥质含量的变化，笔者选用塔里木盆地哈得地区某井4970～5098m一段自然伽玛曲线进行分层。 采样点数N=1024，其深度采样间隔τ=0.125m，截至频率为4(1/m)。

首先，对该段测井曲线进行傅里叶变换,得到其频谱,如图4所示。其频谱曲线具有以下特点:①低频部分谱幅大,高频部分谱幅小,表明测井曲线中低频部分对应的厚层信息较丰富;②低频段谱幅衰减快,而随频率的增高谱幅衰减速度呈下降趋势。笔者通过对同一地区多口井自然伽玛曲线进行频谱分析,发现其频谱曲线具有较大的相似性，这说明在该地区地层分布比较稳定。

对上述自然伽玛曲线用2个图3所示三角形带通滤波器滤波，滤波器参数分别取flow=0.002，fmax=0.02和flow=0.02,fmax=0.2，得到图5所示2条带通滤波曲线，其中频率0.002～0.02(1/m)的滤波曲线对应厚地层，频率0.02～0. 2(1/m)的滤波曲线对应薄地层，进一步采用活度分层法分别对这2条曲线进行地层界面提取，提取结果如图5所示。分层结果与实际结果基本一致，体现了计算的有效性。

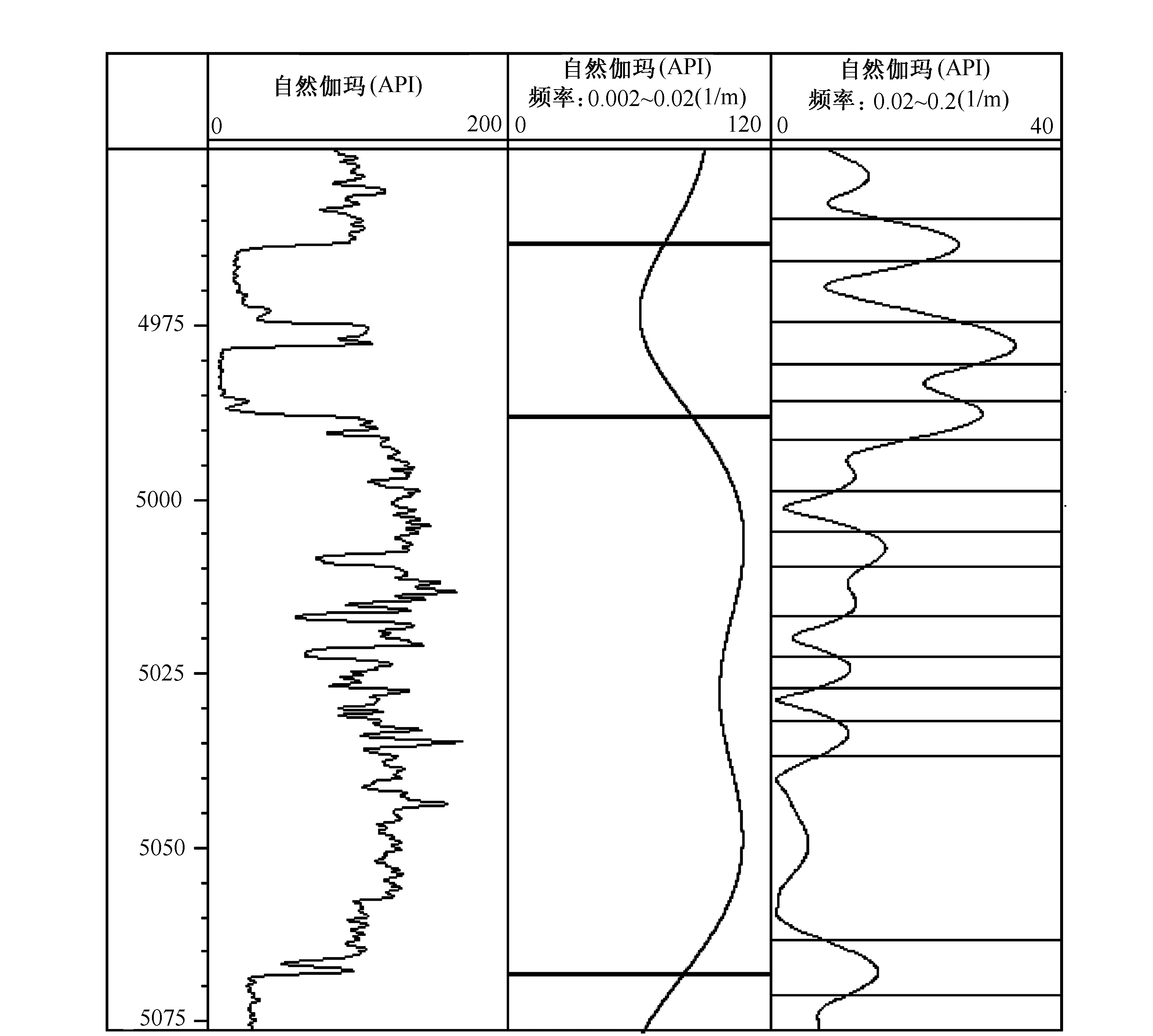
图5 对带通滤波曲线进行分层

4 结 语

利用测井曲线频谱分析对地层进行研究，符合地层周期性沉积规律。通过带通滤波器滤波，可以得到不同尺度的地层旋回特征，从而实现多尺度地质分层。实例研究表明，采用该方法产生的分层结果与实际情况基本吻合。

[1]王贵文,邓清平,唐为清.测井曲线谱分析方法及其在沉积旋回研究中的应用[J].石油勘探与开发, 2002,29(1):93～95.

[2]王红罡,吕炳全,孙小刚.长庆气田储层的高频层序地层学分析[J].同济大学学报,2000, 28(5): 543～546.

[3]易觉非.利用活度分层法实现测井自动地质分层[J].石油天然气学报(江汉石油学院学报),2007,29(1):78～80.

[4]胡广书.数字信号处理[M].北京：清华大学出版社,1997.55～174.

[5]Sophocles J.Orfanidis.Introduction to Signal Processing[M]. 北京：清华大学出版社,1999.541～572.

[编辑] 易国华

P631.84

A

1673-1409(2009)03-N060-03

2009-06-04

易觉非(1966-)，男，1987年大学毕业，讲师，现主要从事应用数学和软件开发方面的教学和研究工作。