开口弧具高阶奇性解Hilbert核方程的求解
陈荆松 (中南财经政法大学信息学院, 湖北 武汉 430073)
陈俊文 (湖北省沙市中学, 湖北 荆州 434000)
开口弧具高阶奇性解Hilbert核方程的求解
陈荆松 (中南财经政法大学信息学院, 湖北 武汉 430073)
陈俊文 (湖北省沙市中学, 湖北 荆州 434000)
在开口弧具高阶奇性解Hilbert核方程完全方程的Nother定理的基础上,通过构造辅助函数,利用基础解系,改写了未知函数在H类(或H*类)情形下特征方程的解,得到了开口弧具高阶奇性解的Hilbert核奇异积分方程的特征方程。
开口弧;高阶奇性;Hilbert核方程;基础解系
关于Cauchy核奇异积分方程的讨论已有较为完备的结论[1~6],特别是开口弧情形的补充[6],使得之前仅限于闭口弧的讨论更加完备。关于Hilbert核情形的奇异积分方程,笔者曾在文献[7]中讨论了其在开口弧具高阶奇性解的积分方程,给出了完全方程的Nother定理,并对解的一般特性作出了描述。下面,笔者将在此基础上对特征方程:

(1)

1 未知函数在H类(或H*类)情形下特征方程解的改写
在H类或H*类情形下,对于方程(1),有:
(i)κgt;0,γ≠或=(2k+1)π时,方程(1)的解分别为:



(2)


(3)
(ii)当κ=0,γ≠(2k+1)π时,方程(1)有唯一解:
φ(t)=N*f+(f1-f0tan(γ/2))B*(t)Z(t)

φ(t)=N*f+CB*(t)Z(t) (C为任意常数)
(iii)当κlt;0,可解条件:
f0sin(γ/2)=f1cos(γ/2)fj-2=fjj=2,…,-κ
正交条件为:

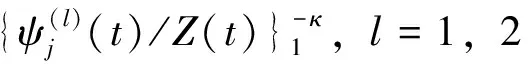

(4)
当γ≠(2κ+1)π时:
φ(t)=K*f-f0tan(γ/2)B*(t)Z(t)=N*f
当γ=(2k+1)π时:
φ(t)=K*f-f1B*(t)Z(t)=N*f
与文献[8]不同,当κlt;0时,得出解的统一表达式及可解条件几何意义明显正交化。
注1上面的讨论对L为开口弧或有节点的曲线亦有类似结果。
2 特征方程的求解
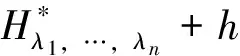
ω(t)=φ(t)-T(tan(t/a))/Π(t)
(5)

这里与闭口弧情形不同之处在于上式中的积分项不易计算出具体值。
但由于F(t)∈H*,由上面的讨论有:
(1)当κgt;0时,方程(1)无条件可解:

(6)
从式(5)得到φ(t)关于ω(t)的表达式后,将式(6)代入得到:

(7)
再由文献[6]有:
(8)


(9)


另一方面,式(8)中:
(10)
将式(9)和式(10)代回式(8)计算后再代回式(7)有:

(11)

(12)
(2)当κ=0时,分以下2种情况:
(i)γ≠(2κ+1)π时,方程(1)有唯一解:


(ii)γ=(2κ+1)π时,当且仅当:
满足时,方程(1)有解:

(3)当κlt;0时,当且仅当条件:
满足时,方程(1)有唯一解式(11)(Pκ(t)≡0)。
[1]路见可. 沿曲线的积分方程,其解具有一阶奇性[J]. 武汉大学学报(自然科学版),1964,(1):1~13.
[2]路见可,张桂生. 具一阶奇性解的奇异积分方程[J]. 武汉大学学报(自然科学版),1997,43(3):273~280.
[3]钟寿国,赵新泉. 具高阶奇性解的奇异积分方程(I)[J]. 武汉大学学报(自然科学版),1997,43(5):553~559.
[4]钟寿国,赵新泉. 具高阶奇性解的特征奇异积分方程(II)[J]. 武汉大学学报(自然科学版),1998,44(1):5~10.
[5]钟寿国. 具高阶奇性解的奇异积分方程的推广Noether定理[J]. 数学年刊, 1998,13A(3):361~366.
[6]Zhong Shou-guo. Singular integral equations along an open arc with solution having singularities of higher order[J]. Acta Mathematica Scientia, 2005,25B(2):193~200.
[7]陈荆松,钟寿国,陈俊文.开口弧具高阶奇性解的Hilbert核奇异积分方程[J].长江大学学报(自然科学版),2008,5(1):N10~12.
[8]路见可. 周期Riemann边值问题及其在弹性力学中的应用[J]. 数学学报, 1963, 3(3):343~388.
[编辑] 洪云飞
O175.8
A
1673-1409(2009)01-N005-03
2008-12-26
国家自然科学基金项目(10471107)。
陈荆松(1979-),男,2000年大学毕业,博士,讲师,现主要从事复分析理论方面的教学与研究工作。

