学生创新能力培养的返璞归真

黄胜强

不少教师在操作层面对培养学生创新能力的方式、途径“上下求索”,并取得一些令人欣慰的成果,但“孔雀开屏的背后”——“远离教材背景,海阔天空搞创新”或“忽视可接受性原则,拔苗助长搞创新”或“头重脚轻根底浅,忽视双基夯实搞创新”等误区也不容忽视,笔者认为,“务实阶段”求真务实的数学教学应在“应对考试”与“素质教育”之间寻找平衡、追求磨合,尤其是对学生创新能力培养问题上,应极力倡导返璞归真。

一、营造宽松心理环境,激活创新的潜意识

“橘生淮南则为橘,生于淮北则为枳”,其原因:水土异也,气候异也,环境异也,鲁迅先生也曾批判:中国从来不缺天才,缺的是适合天才生长的土壤,换而言之,发明创新是人的一种天性、一种潜意识,这种天性、潜意识就如“星星之火”,要使这种“星星之火”形成“燎原之势”,最需要的是一种宽松的心理环境。

“教师是人类灵魂的工程师.”,在笔者看来,其实每一个“灵魂”就像一个个体积一样的糍粑,有凹下去的地方就必有凸出的地方,反之亦然,所谓:“以生为本”“尊重差异”,最朴素的解读也就是:我们对学生“凹下去的地方”应当正视,而最关键的是去发现、关注并呵护“凸出来的地方”,信念并实践“好孩子是夸出来的”。

因此,我在教学过程中常用“错了不要紧,只要你认真” “不论你的观点正确与否都备受尊重” “其实即使天才,在生下来的时候的第一声啼哭,也和平常的儿童一样,决不会就是一种好诗”和“我们都是新生事物的促进派,我们永远支持你”等语言激发学生暴露自己真实的想法、做法,展示自己的创意。

二、回溯数学文化本源,浸润创新文化底蕴

数学教学应返璞归真,树立一种文化寻根意识,针对具体教学内容,回溯数学文化本源,厘清它的来龙去脉,创设鲜活的在人文与理性磨合中“分娩”的情境——化“冰冷的美丽”为“火热的思考”,相应地让数学批判创新的文化底蕴,“随风潜入夜”,浸润学生的“灵魂”。

如异面直线概念的教学,我们可创设如下问题情境。

1. 直线AB与A′B′的位置关系是_____。

2. 直线AB与B′C′的位置关系是_____。

3. 直线AB与D′C′的位置关系是_____。

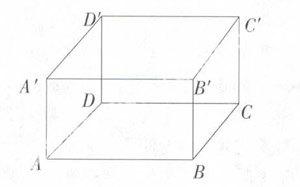
[有点“水中望月,雾里看花”的感觉,我们常说“曲径通幽”,AB与A′B′的位置关系如何?(平行)AB与D′C′的位置关系如何?(平行)因此,AB与D′C′是平行的,几何上的平行是可传递的——犹如爱的传递一样,事实上,我们看它们尽管当前不在同一平面,但一旦连结AD′,BC′,便可一睹其“尊容”:在同一平面,且不相交。]

4. AB与B′C′的位置关系呢?

[平行说不上,相交也不妥,总之,既不相交也不平行,换句话说,它们不仅当前不在同一平面内,而且永远不能在同一平面内。]

5. 你还能在图中找出哪些直线间有类似AB与B′C′的这种位置关系?我们教室中的哪些实物间有类似AB与B′C′的这种位置关系?

6.在我们数学世界里有个惯例:对于这种不能纳入以往关系分类体系中的关系,就必须用新的术语来刻划这种新关系以示区别,你能尝试用一个的新术语简洁明了而形象地刻划这样的关系吗?

[数学家们用“异面直线”这个术语来刻划其本质:既不相交也不平行,即,不仅当前不在同一平面,而且永远不能在同一平面的直线。]

三、适度改编教材习题,寓创新于双基之中

对教材习题中一些“意犹未尽”的问题,遵循可接受性原则适度变式,在探究性过程中让某种规律、特殊情形淋漓尽致地彰显出来,可深化认识,发展数学真理——寓创新于双基夯实之中。

例如,针对八年级几何第179页“求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形”可创设这样的探究问题:依次连结①平行四边形②矩形③菱形④正方形⑤等腰梯形⑥直角梯形⑦对角线相等的四边形⑧对角线垂直的四边形⑨对角线相等且互相垂直的四边形,中点将分别得到什么样的四边形?新四边形对角线的长度、位置关系分别由什么决定?新四边形是正方形可肯定原四边形的对角线一定具备什么特点?

这样,由点及面,对各种四边形的共性与个性展开更深层探讨,把“顺次连结四边形四条边的中点,所得的四边形是平行四边形”,发展为“顺次连结四边形四条边的中点所得的新四边形的特点,由原四边形对角线的长度关系与位置关系决定;对角线长度相等,则新四边形四条边相等;对角线互相垂直,则新四边形四条边互相垂直”。

责任编辑 罗 峰