粘弹性地基中管桩的纵向振动特性研究

丁选明，陈磊

粘弹性地基中管桩的纵向振动特性研究

丁选明1，2，陈磊2

（1．长江科学院水利部岩土力学与工程重点实验室，武汉430010；2．河海大学岩土工程科学研究所，南京210098）

基于经典的平面应变假定，推导出了管桩动力响应的频域解析表达式。分析了土体剪切模量、阻尼系数、桩芯土、桩径等对振动特性的影响。计算结果表明：土体剪切模量越大，速度导纳曲线和复动刚度曲线振荡幅值越小；土体阻尼系数越大，速度导纳曲线振荡幅值越小；桩周土对桩壁的摩阻力要比桩芯土大；桩径越小，桩芯土对桩的作用力越小。

管桩；粘弹性地基；动刚度；速度导纳；动力响应

现浇混凝土薄壁管桩广泛应用于高速公路、市政道路的软基加固工程中［1～3］。在工程应用中，会出现各种各样的动力问题，如桩基的动力检测、交通荷载等动荷载作用下桩的动力响应等。这些动力问题的解决需要桩基振动理论的支持。运用子结构方法对桩-土-结构相互作用体系进行动力分析时，遇到的关键问题之一是合理地确定桩基的动力阻抗［4］，如果能确定桩-土系统的动刚度和阻尼，那么桩支承上部结构的动力响应就能计算出来［5］。因此研究现浇薄壁管桩的纵向振动特性具有重要的理论意义和工程应用价值。

Novak等［6～8］假定土体由径向无限延伸的薄层组成，层与层之间相互独立，桩土之间位移协调，推导出了实心桩桩顶复阻抗函数的解析表达式，这就是经典的平面应变解。国内外学者对桩基振动理论的研究主要是针对实心桩，对管桩振动理论的研究主要采用的数值方法，在解析解方面成果较少。

本文将经典的平面应变解推广应用到管桩，推导出了现浇薄壁管桩动力响应的解析表达式，丰富了桩基动力学的理论，为现浇薄壁管桩的动力测试和振动特性分析提供了理论支持。还研究了桩周土和桩芯土性质对动力特性的影响，得到的结论具有一定的工程实用价值。

1 计算模型

本文采用了如下基本假定：①桩周土和桩芯土为一系列相互独立的薄层组成，忽略土层之间的相互作用；②桩身混凝土为线弹性材料；③桩与桩周土和桩芯土界面位移协调；④桩周土和桩芯土为均匀粘弹性体，用Voigt模型表示；⑤桩土体系的纵向耦合振动时，忽略土体的水平径向位移；⑥桩土系统振动为小变形。

图1给出了计算模型。桩长为H，内半径r2，外半径r1。桩周土Lame常数为λ1、G1，密度ρ1，粘性阻尼系数为η1。桩芯土Lame常数为λ2、G2，密度ρ2，粘性阻尼系数为η2。桩底土对桩作用刚度系数为kp，阻尼系数为δp。

图1 计算模型Fig．1 Computational model

2 理论解的推导

运用弹性动力学的基本理论，容易建立平面应变条件下土体的振动方程为

对方程（1）进行Laplace变换得

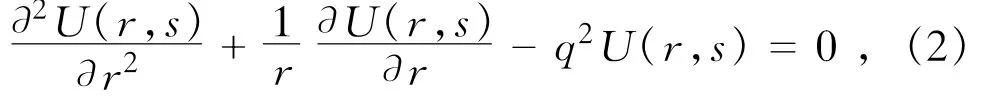
式中：U（r，s）为u（r，t）的Laplace变换，q2＝ρs2／（G＋ηs）。

方程（2）的通解为

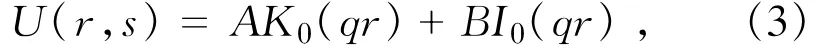
式中：A，B为待定常数；K0，I0为变形的Bessel函数。

对于桩周土体，由于无穷远处位移为0，因此I0的系数为0，桩周土位移可表示为

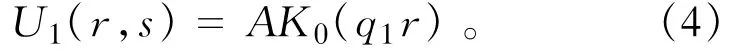
对于桩芯土体，由于r＝0时位移为有限值，因此K0的系数为0，桩芯土位移可表示为

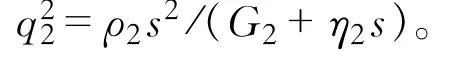
利用桩-土位移连续条件可得：

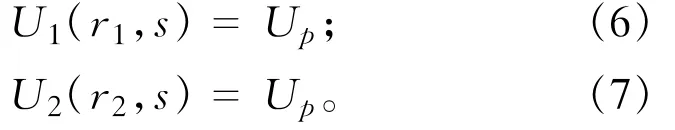
将（4）、（5）代入（6）、（7）可得：

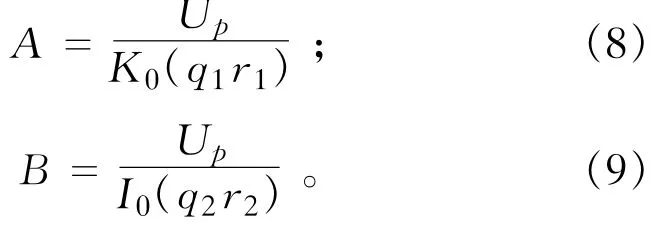
桩土接触面的剪应力为：

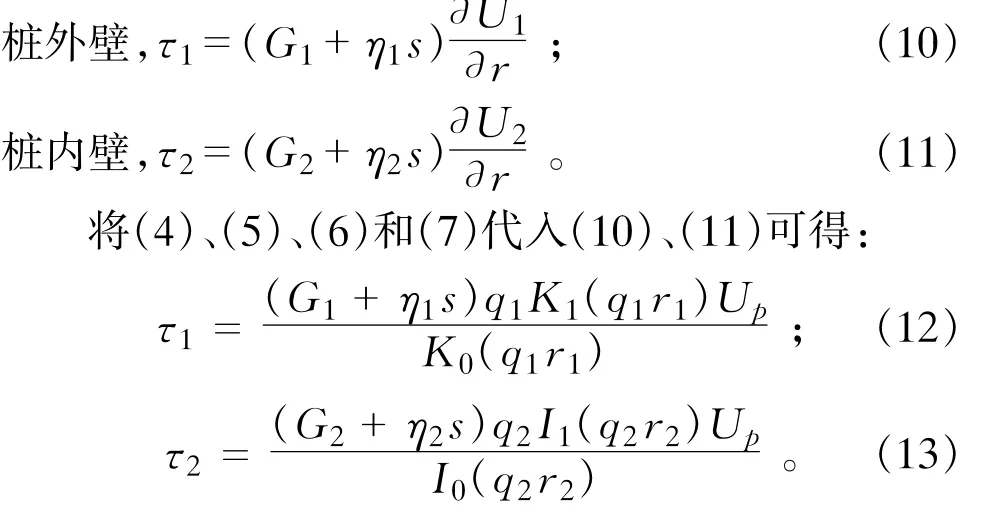
桩的振动方程为

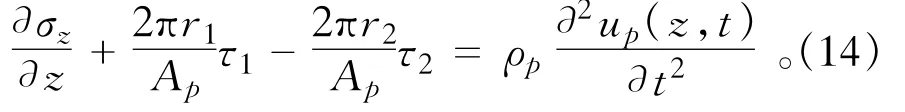
式中：Ap为桩身截面积，ρp为桩身混凝土密度。

将方程（14）应力用位移表示，再进行Laplace变换，并将（12）、（13）代入，可得

式中Up（z，s）为up（z，t）的Laplace变换，

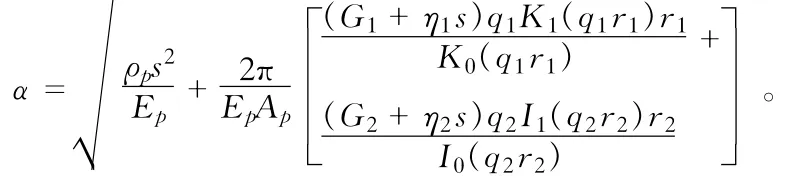
其中，Ep为桩身弹模。

从方程（15）可以解得

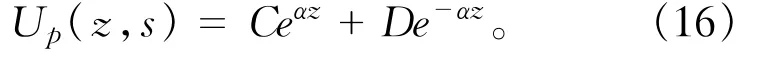
式中C，D为待定系数。

假定桩顶作用一力p（t），它的Laplace变换为P（s），那么桩顶边界条件为

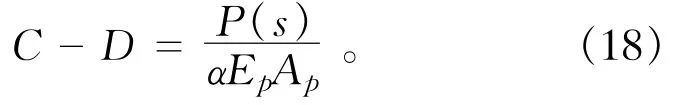
Laplace域内，桩底边界条件可表示为

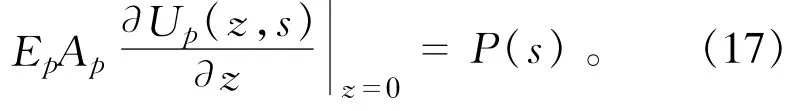
将（16）代入，可得

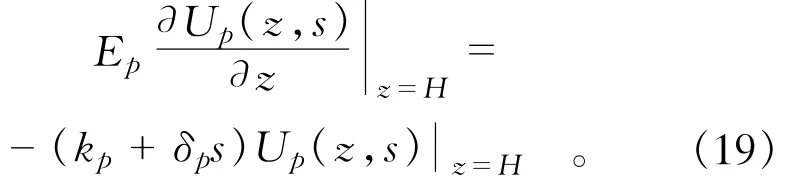
将（16）代入，可得

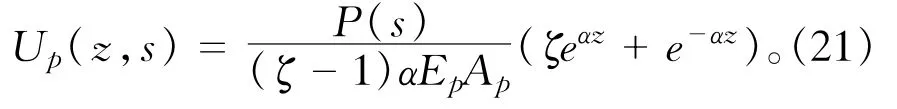
式中，令s＝iω，则Laplace变换相当于单边的Fourier变换，因此可以得到位移频域响应为Up（z，iω）。

可得到桩顶复动刚度的表达式为

由（18）、（20）就可以求出待定系数C，D，再将C，D代入（16），得到桩位移表达式为

桩顶速度导纳的表达式为

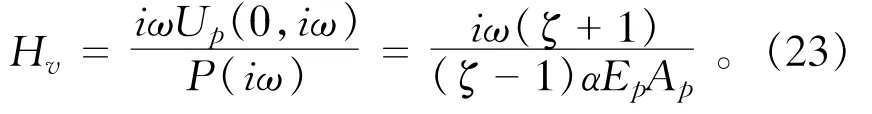
3 算例分析

下面采用本文提出的方法对桩顶振动特性进行分析。本算例中，桩长10 m，外直径1．0 m，壁厚12 cm，桩身混凝土弹模25 GPa，密度2 400 kg／m3，桩底刚度系数1．0E6N／m3，阻尼系数1．0E5Ns／m3。

3．1土体剪切模量的影响

为了研究土体剪切模量对动力响应的影响，计算了剪切模量分别为2，5，10 MPa 3种工况，土体粘性阻尼系数都取为10 000 Ns／m2，桩芯土和桩周土参数相同。

图2给出了不同土体剪切模量的桩顶速度导纳比较。从图可以看出，速度导纳曲线来回振荡，每隔一定的频率达到峰值。频率较低时振荡幅值较大，随着频率的增加，振荡幅值减小，高频时接近一水平直线。土体剪切模量越大，土对桩侧壁的剪应力越大，因此振荡幅值越小。图3和图4为不同土体剪切模量的桩顶复动刚度实部和虚部。实部代表真实的刚度，虚部代表了阻尼。土体剪切模量对复动刚度的影响与速度导纳类似，剪切模量越大，振荡幅值越小。图中2 MPa曲线的振荡幅值最大，10 MPa曲线的最小，5 MPa曲线的介于两者之间。

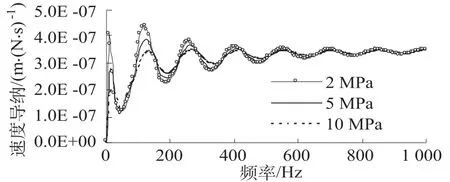
图2 不同土体剪切模量的桩顶速度导纳Fig．2 Velocity admittance on top of the pile with different soil shear moduli

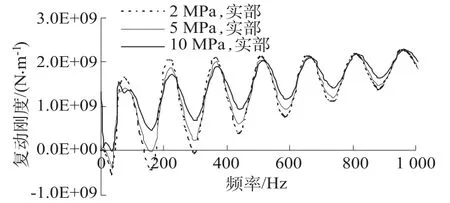
图3 不同土体剪切模量的桩顶动刚度实部Fig．3 The real part of dynamic stiffness on top of the pile with different soil shear moduli

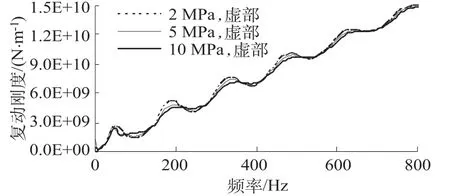
图4 不同土体剪切模量的桩顶动刚度虚部Fig．4 The imaginary part of dynamic stiffness on top of the pile with different soil shear moduli

3．2土体阻尼系数的影响

土体阻尼系数对管桩动力响应有影响。本算例计算了阻尼系数分别为5 000，10 000，20 000 Ns／m2的情况。计算中土体剪切模量为5 MPa，桩芯土和桩周土参数相同。

图5为不同土体阻尼系数的桩顶速度导纳曲线。阻尼系数越大，土对桩的作用力也越大，因此速度导纳振荡幅值越小。图中阻尼系数5 000 Ns／m2的曲线振荡幅值最大，10 000 Ns／m2的次之，20 000 Ns／m2的最小。

3．3桩芯土的影响

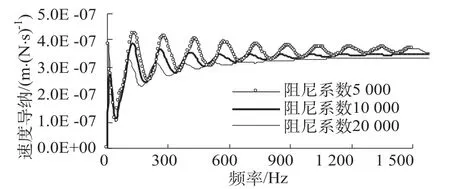
图5 不同土体阻尼系数的桩顶速度导纳Fig．5 Velocity admittance on top of the pile with different soil damping coefficients

管桩与实心桩的不同之处是存在桩芯土的作用，在桩顶动荷载的作用下，桩周土和桩芯土都对桩有摩阻力作用。为了研究桩周土摩阻力和桩芯土摩阻力的影响大小，计算了不考虑桩芯土、不考虑周土和两者同时考虑的桩顶动力响应。计算中，土体剪切模量取5 MPa，阻尼系数取10 000 Ns／m2。

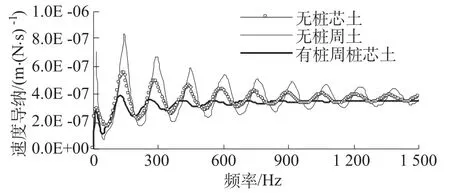
图6 桩周土和桩芯土存在与否对桩顶速度导纳的影响Fig．6 The effect of surrounding soil and inner soil on velocity admittance on top of the pile

图7 桩周土和桩芯土存在与否对桩顶动刚度实部的影响Fig．7 The effect of surrounding soil and inner soil on the real part of dynamic stiffness on top of the pile

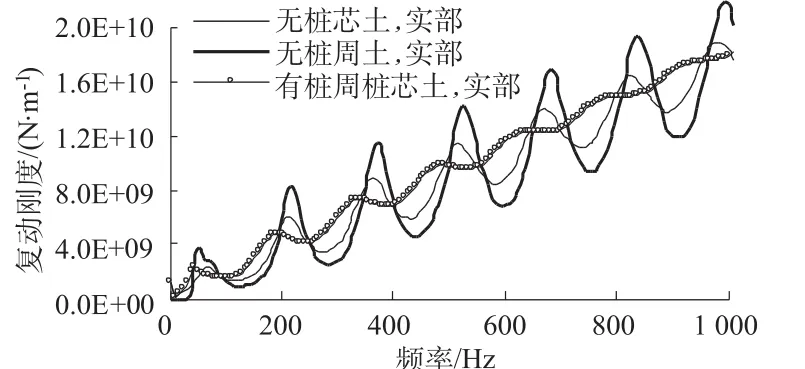
图8桩周土和桩芯土存在与否对桩顶动刚度虚部的影响Fig．8 The effect of surrounding soil and inner soil on the imaginary part of dynamic stiffness on top of the pile

图6 为各计算工况的桩顶速度导纳曲线。从图可知，无桩周土时速度导纳振荡幅值最大，无桩芯土时次之，而桩周土和桩芯土都存在时最小。图7和图8复动刚度也有相同的规律。可见，桩周土对桩壁的摩阻力要比桩芯土大，使得无桩芯土（仅有桩周土）时的振荡幅值比无桩周土（仅有桩芯土）时的小。桩芯土对桩的作用力受半径的影响很大。图9和图10分别为桩径0．6 m和0．4 m管桩的桩顶速度导纳曲线。图9和图10中曲线的规律与图6（桩径1．0 m）有一定的区别。图6由于桩径较大，桩芯土对桩的作用力也相对较大，因此有桩芯土（有桩周土）时曲线的振荡幅值要比无桩芯土（有桩周土）时的明显小很多。而图9和图10桩径较小，因此有桩芯土时的曲线和无桩芯土时的曲线差别不大，图10中两条曲线基本重合，说明桩芯土对桩基本没有作用力。以上分析表明，桩径越小，桩芯土对桩的作用力越小，桩径足够小时，桩芯土对桩的作用力基本可以忽略。

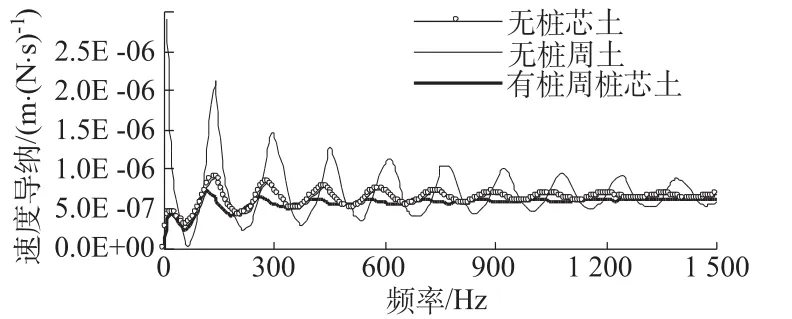
图9 桩径0．6 m管桩土体存在与否对桩顶速度导纳的影响Fig．9 The effect of existence of the soil on velocityadmittance on top of the pile with 0．6m diameter

4 结论

本文将经典的平面应变解推广应用到管桩，丰富了桩基动力学的理论，得到的结论具有一定的工程意义。主要结论如下：

（1）速度导纳曲线和复动刚度曲线来回振荡，每隔一定的频率达到峰值。频率增加，振荡幅值减小，高频时接近一水平直线。土体剪切模量越大，因此振荡幅值越小。

（2）土体阻尼系数越大，土对桩的作用力也越大，速度导纳曲线振荡幅值越小。

（3）桩周土对桩壁的摩阻力要比桩芯土大。桩径越小，桩芯土对桩的作用力越小，桩径足够小时，桩芯土对桩的作用力基本可以忽略。

［1］刘汉龙，费康，马晓辉，等．振动沉模大直径现浇薄壁管桩技术及其应用（Ⅰ）开发研制与设计［J］．岩土力学，2003，24（2）：164-168．

［2］刘汉龙，郝小员，费康，等．振动沉模大直径现浇薄壁管桩技术及其应用（Ⅱ）工程应用与现场试验［J］．岩土力学，2003，24（3）：372-375．

［3］杨寿松，刘汉龙，周云东，等．薄壁管桩在高速公路软基处理中的应用［J］．岩土工程学报，2004，26（6）：750-755．

［4］栾茂田，孔德森．单桩竖向动力阻抗计算方法及其影响因素分析［J］．振动工程学报，2004，17（4）：500-505．

［5］NOVAK M．Dynamic Stiffness and Damping of Piles［J］．Canada Geotechnical Journal，1974，（11）：574-598．

［6］NOVAK M．Vertical Vibration of Floating Piles［J］．Journal of the Engineering Mechanics Division，ASCE，1977，103（EM1）：153-168．

［7］NOVAK M，ABOUL-ELLA F．Impedance Function of Pilesin Layered Media［J］．Journal of the Engineering Mechanics Division，ASCE，1978，104（EM3）：643-661．

［8］NOVAK M，NOGAMI T，ABOUL-ELLA F．Dynamics Soil Reactions for Plane Strain Case［J］．Journal of the Engineering Mechanics Division，ASCE，1978，104（EM4）：953-959．

（编辑：曾小汉）

Study on Vertical Vibration Characteristics of Pipe Piles in Viscoelastic Soil

DING Xuan-ming1，2，CHEN Lei2
（1．Key Laboratory of Geotechnical Mechanics and Engineering of the Ministry of Water Resources，Yangtze River Scientific Research Institute，Wuhan 430010，China；2．Geotechnical Research Institute，Hohai University，Nanjing 210098，China）

On the basis of classical plane strain case，the analytical solution on dynamic response of pipe pile in frequency domain was derived．The influences of soil shear modulus，damping coefficient，inner soil and diameter on vibration characteristics were studied．Numerical results indicated as follows：The oscillating amplitude of velocity admittance curve and dynamic complex stiffness curve is reduced with the increase of soil shear modulus and damping coefficient．The frictional resistance of outer soil is larger than that of the inner soil．The resistance of inner soil is reduced with the decrease of pile diameter．

pipe pile；viscoelastic soil；dynamic stiffness；velocity admittance；dynamic response

TU472．3

A

1001-5485（2009）03-0032-04

2008-03-18

丁选明（1980-），男，湖南宁乡人，博士，主要从事桩基动力学方面的研究，（电话）13813953213（电子信箱）dxming＠hhu．edu．cn。