在数学训练中促使学生顿悟的策略

黄九林

顿悟是指突然觉察到问题的解决办法，它是通过学习者重新组织或重新建构有关事物的形式而实现的。顿悟既可以避免多余的尝试错误，又能促进知识的迁移运用。在数学教学过程中，重视学生思维顿悟的训练，对提高教学效率有着重要的意义，它既是促使训练到位：提高学生数学素质的必要操作规程，也是构成课堂教学过程不可缺少的环节。

一、追本溯源——在倒摄处促其顿悟

很多学生在解题时，往往根据例题的解法照葫芦画瓢，对解题的思路和方法知其然，而不知其所以然

因此，教师不能只满足于学生解答出一个正确结果，而应当启发学生反思解题的思路，倒摄答案形成的过程，获得思维的顿悟。

例如：“立新化肥厂全年计划生产化肥1500吨，实际上半年每月生产化肥147.6吨，剩下的要4个月完成，平均每个月生产化肥多少吨?”学生解题后，教师指着综合算式：(1500-147.6×6)÷4追问：“你是怎样分析这道题的数量关系的?”

这关键的一问，可以启发学生反思，把解题的思维过程暴露出来。然后继续追问：(1)147.6×6求出什么?(2)1500-147.6×6求出什么?(3)整个算式求出什么?通过这样有层次的追问，能使学生进一步反思算理，掌握应用题的结构和解题思路。

二、小题大做——在细微处促其顿悟

教材中有些细微处是十分丰富的思维素材，教师要善于“小题大做”，在“细微”处促其思维顿悟，达到训练的目的。

如教学“三角形面积公式”的推导过程时，我针对教材所述“两个完全一样的三角形可以拼成一个平行四边形”

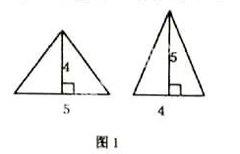
启发学生思考：能否将“两个完全一样”换成“两个面积相等”，为什么?有一部分同学认为“可以”，理由是“两个完全一样”的三角形面积是相等的，而另一部分学生则说：“不可以”，因为“面积相等”的两个三角形，不一定是“完全一样”的，而两个不完全一样的三角形是不可能拼成一个平行四边形的。如下图1：

这两个三角形虽然面积相等，但无法拼成一个平行四边形。我又进一步追问：能否换成“两个等底等高”的三角形呢?学生经过思考，都认为不能，理由是“两个等底等高”的三角形不一定是“完全一样”的三角形。如下图2中ABC和DBC虽然等底等高，但不能拼成一个平行四边形。

在教材的细微处引导学生反思，成就了学生思维顿悟的良好契机，正是在顿悟的过程中，学生的分析能力和应变能力得到了有效的训练。

三、水到渠成——在铺垫处促其顿悟

有些应用题的数量关系比较复杂，学生很难找到解题的突破口，这就需要教师设计必要的铺垫，以减缓思维坡度，促其思维顿悟，让学生顺利从未知过渡到已知。

如，有这样一道题：“为了鼓励节约用电，某市电力公司规定了以下电费计算方法：每月用电不超过100千瓦时，按每千瓦时0.52元收费；每月用电超过100千瓦时，超过部分按每千瓦时0.6元收费。小明家10月份付电费64.6元。用电多少千瓦时?”教学时

可设计以下一系列问题作为铺垫：

如果小明家用电正好是100千瓦时，应付电费多少元?[0.52×100=52(元)]

2、小明家实际超出电费多少元?[64.6-52=12.6(元)]

3、这说明小明家用电已超过多少千瓦时?[100千瓦时]

4、超出部分每千瓦时0.6元，多少千瓦时才是12.6元呢?[12.6+0.6=21(千瓦时)]

5、小明家一共用电多少千瓦时?[100+21=121(千瓦时)]

由于教师的设问由浅入深，一步一步推进，促进了学生对解题思路的顿悟。

四、各抒己见——在补白处促其顿悟

艺术家的创作手法都讲究“留白”，让人们发挥想象去填补。在教学过程中，如果教师能够设计一些填充题，激发学生的想象来填补这些空白，实质上也就是充分展示了学生对这类问题的顿悟过程。

如在复习分数应用题时，可在巩固练习中设计补充条件的题目。如：在下面的横线上，补充一句带有分率的话，使它成为一道完整的分数应用题(至少补充3种不同的形式)。

五(1)班男生有30人，______，女生有多少人?这道题横线上的填法有：女生是男生的2/3；男生是女生的3/2；男生比女生多1/2；女生比男生少1/3；男生占全班的3/5；女生占全班的三；女生比男生的5/6少5人；比女生的3/4多15人……

通过这样的“补白”，进一步强化了学生对“分数应用题的结构”和“单位1”表现形式的顿悟，训练了学生自觉联想和快速转化的能力。

五、亡羊补牢——在救失处促其顿悟

教师在为学生匡谬救失时，要重视展现思维过程，以便从深层次上作出诊断和矫治。在解题过程中，学生的思维偏差往往带有很强的主观性，又具有普遍性，抓住这些失误和偏差进行剖析，不仅能补救误差。而且能够促使学生进行深层次的思维顿悟。

例如：“抄一份稿件，甲单独抄要1/2小时完成，乙单独抄要1/3小时完成。现两人合抄，多少小时完成?”大部分学生的解法是：1/2x+1/3x=1或1÷(1/2+1/3)，学生出错的原因是受“工作效率”表现形式的干扰，误认为1/2和1/3分别是甲和乙的工作效率。针对出错原因，可引导学生思考“1/2表示什么?1/3表示什么?甲和乙的工作效率各应怎么求?”以此让学生重新审题，明白自己的错误所在，即把“分数形式的工作时间”误认为是工作效率了。

六、举一反三——在变式处促其顿悟

对教材中的重点和难点，必须加大训练力度。因此教师要适当插入一些变式训练，使学生在突破重难点的思维过程得到顿悟。

如在教学“三角形内角和”这部分知识时，为了讲清“三角形内角和是180度”的道理，可引导学生运用多种方法加以证明：(1)度量法：用量角器把三个角度的数量出来，然后相加和是180度；(2)剪拼法：把一个任意三角形纸片的三个角剪下来，然后拼到一起，刚好拼成一个平角，所以三角形内角和是180度；(3)推算法；将一个长方形(或正方形)沿对角线剪开，得到两个完全一样的三角形，因为长方形的四个角者90度，内角和是360度，所以每个三角形的内角和是360+2=180度。

七、能言善辩——在讨论处促其顿悟

当学生解题出现多个答案时，教师不要急于断言对或错，而要引导学生进行讨论、交流，这样把学生肤浅、模糊的认识变得清楚深刻。让学生在比较中对各种答案进行辨析，对各种算法进行分类、提炼，从而达到对这些知识的深层次的顿悟。

例如：“一张靶纸共三圈，投中内圈得10环，投中中圈得8环，投中外圈得6环，小华投中两次可能得到多少环?”学生的回答出现了两种答案：第一种是“5种可能”，第二种是“6种可能”。此时教师不急于评价，引导学生讨论。认为5种可能的学生在讨论时说，我们是从得分的高低来列出各种可能的，小华投中两次，最低可得12环(6+6)，最高可得20环(10+10)，中间还可得14环(8+6)、16环(8+8、10+6)和18环(10+8)，所以是5种可能。而另一部分学生说，我们是按照投中的可能性来列举的：外圈和外圈(6+6)，外圈和中圈(6+8)，外圈和内圈(6+lO)，中圈和中圈(8+8)，中圈和内圈(8+10)，内圈和内圈(10+10)，所以是六种可能。经过一番辩论，最后错误的一方找出了问题的症结：我们错误的原因是把得分的几种可能和命中的几种可能混淆起来了，而其中命中“中圈和中圈、内圈和外圈”的得分数都是16，我们却把它们作为两种不同的得分来算，所以产生了错误。

八、借题发挥——在延伸处促其顿悟

学生在解题过程中常出现这样的现象：题目做完了，但思维过程还没完，教师若能抓住这种机会，在延伸处促其思维顿悟，也是很有训练价值的。

如，有这样一道题：

0.3×0.3=

0.33×0.33=

0.333×0.333=

0.3333×0.3333=

0.33333×0.33333=

第一个算式的结果是0.09，第二个算式的结果是0.1089，其他各式自上而下在0(小数部分)的左边依次多个1，而右边依次多个8，教学这道题时，我首先引导学生观察前三道式子相互之间有什么关系，通过计算得数有什么规律。然后引导学生根据上面的规律来预测下面两道式子的结果分别是什么。在此基础上，我进一步启发学生思考：如果得数是0.11111108888889，你能推想出算式该是什么吗?这样，学生就能自己归纳出算式：0.3333333×0.3333333。

责任编辑：曹文