巧妙设计问题 提高学生能力

支　华

[关键词]问题；设计；趣味型；创新型；应用型；探索型

[中图分类号]G633.6[文献标识码]A

[文章编号]1004-0463(2009)05(A)-0044-01

设计趣味性问題，培养学生的认知能力

学生是课堂的主体，兴趣是最好的“老师”，教师只有激发了学生的兴趣，才能调动起学生的积极性、主动性，故而，教师要利用学生熟悉的生活情境和感兴趣的事物作为教学活动的切入点，使学生对问题产生极大的兴趣，从而为研究问题、解决问题提供了基础、动力和保证。

如，在教学“数轴”的概念时，笔者设计了一个“一条东西向的笔直公路上出现了车祸，我们该如何报警?”的问题，建立了“如何确定直线上一点的位置”的教学模型，学生依据生活经验，通过讨论、画图，很快地抽象出了“数轴”的概念，并理解了“方向、原点、单位长度是数轴的三要素，缺一不可”，

通过“问题—探索—解决—新问题—再探索—再解决”这些教学环节，不仅体现了学生是学习的主人的理念，还提高了学生的认知能力。

设计创新型问题，培养学生发现问题的能力

学生认识的过程就是学生观念上的平衡状态不断遭到破坏，并不断达到新的平衡状态的过程，因此，教师所设计的问题应引发学生认知上的不平衡，从而让学生清楚地看到自身已有知识的局限性，产生要通过新的学习活动，达到新的、更高的平衡的欲望，

如，教学“负数”时，笔者设计了“知识竞赛”的问题，评分标准是：答对一道题加10分，答错一道题扣10分，不回答得。分，每个代表队的基础分为0分，现有4个代表队回答5道题，让学生与同伴进行讨论：每个代表队最高成绩是多少分?最低成绩是多少分?这样在讨论的过程中，学生发现有可能某一代表队答对的题目数量少于答错的题目数量，就需要从基础分里扣分，从而自然地引，出负数的概念，这样设置问题，激发了学生新的需要与储备知识缺乏之间的冲突，从而培养了学生的学习动机和发现问题的能力。

设计应用型问题，培养学生答疑释难的能力

教学时，教师应设法为学生创设逼真的问题情境，激发学生思考的欲望，让学生体验数学学习与实际生活的联系，体会到用所学知识解释生活现象和实际问题的乐趣。

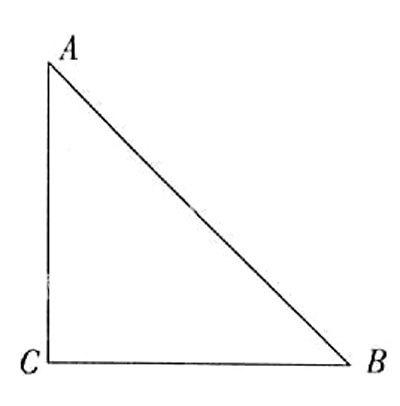
如，在教学“平行线等分线段定理”时，笔者设计了这样一道实际问题：如右图，有直角三角形的菜地ACB分给张、王、李三家，C是三家合用的肥料仓库，AB是水渠，分配条件是：三户分得的菜地面积相等，每户必有一部分菜地紧靠水渠，请你用尺规在图中作出各家菜地的分界线，对于该问题学生只要根据同底等高的三角形面积相等的原理，就能把找相等的底的问题转化为如何对线段AB进行三等分的问题，而这又恰恰是本节课所要研究的中心问题，这样既激发了学生求知的欲望，又把数学知识如何为生活服务直接展示给学生，从而提高了学生解决实际问题的能力。

设计探索型问题，培养学生动手操作的能力

数学知识并非是纯理论性的，有时必须通过具体的实验进行观察、讨论、交流、归纳、猜想、分析和整理，才能提出数学问题，形成数学概念，获得数学结论。

如，在教学“过三点的圆”时，可引导学生动手，让学生在探索的过程中领悟知识，教师可依次安排这样几个问题，让学生通过动手画图探索得出结论，

探索1：过一点的圆，①在平面内有一点O，过点O能否作一个圆?能作几个?②如何确定过点O的圆的圆心?

探索2：过两点的圓，在平面内有两点A、B，你能作出过丸、B两点的圆吗?能作出几个?可让基础较好的学生回答：作圆的关键是什么?要作过A、B两点的圓，圆心到A、B两点的距离有什么关系?什么样的点到线段AB的距离相等?以此为学生探索问题提供思路，

探索3：过三点的圆，分析三点的位置，让学生讨论：过同一直线上的三点能作圆吗7能作几个?不在同一直线上的三点能作圆吗?能作几个?为了强调必须是不在同一直线上的三点才能作圆，用反证法证“过同一直线上的三点不能作圓”，并且由学生自己讲解，在以上整个探索的过程中，要注意让学生自己动手、动脑，最终得出正确的结论。

设计问题的方法还有很多，如，设计类比型问题，培养学生类比、归纳的能力；设计悬念型问题，引导学生积极、主动地学习，总之，问题设计是教师必须重视的研究课题，但不管哪一种问题的设计，必须具有导向性和针对性。