一类两种群均有收获率的HollingII类生物捕食系统的定性分析

何德明,窦霁红,何万生

(1.天水师范学院数学与统计学院,甘肃天水 741000;2.西北大学数学系,陕西西安 710069)

一类两种群均有收获率的HollingII类生物捕食系统的定性分析

何德明1,窦霁红2,何万生1

(1.天水师范学院数学与统计学院,甘肃天水 741000;2.西北大学数学系,陕西西安 710069)

对一类两种群均有收获率的具HollingII类功能反应的食饵-捕食系统作定性分析,利用常微分方程定性,稳定性及分支理论,得到此类生物捕食系统平衡点的性态和极限环的存在,不存在的条件及开发研究的结论,补充和完善了前人的结果.

细焦点;极限环;存在性

1 引言

对于具有常数收获率(或者无收获率)和功能反应的食饵-捕食两种群模型的研究较多[13],但对于两种群均有非常数收获率的研究相对较少.本文将研究食饵种群具有非线性密度制约而捕食种群和食饵种群同时具有非常数收获率和HollingII类功能反应的食饵-捕食两种群模型

上述方程中E是对两种群捕捞强度,q1,q2分别表示对两种群的收获率.

基于系统的生态意义,以下讨论仅在¯G={(x,y)|x≥0,y≥0}中进行.

2 化简模型

3 平衡点及其性态

4 极限环的不存在性

5 极限环的存在性

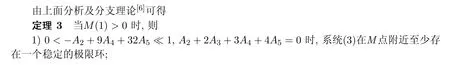
2)0＜−A2+9A4+32A5≪1,A2+2A3+3A4+4A5＜0时,系统(3)在M点附近至少存在两个极限环.

证明当A2+2A3+3A4+4A5=0时,−A2+9A4+32A5=0,则M为二阶稳定的细焦点,而−A2+9A4+32A5＞0时,则M为一阶不稳定的细焦点,稳定性发生反转,在点M的领域中跳出一个稳定的极限环,所以结论1)成立.而当−A2+9A4+32A5＜0时,点M又变为稳定的粗焦点,稳定性发生反转,在点M的领域中跳出第二个极限环,所以结论2)成立.

6 极限环存在与否时,收获率所应满足的条件

极限环对应着生态系统的周期运动,它的存在与否对人们的生产生活具有重要意义.若系统存在极限环,则食饵与捕食者可以达到振荡平衡状态;而不存在极限环,就有可能食饵或者捕食者走向灭绝,这是我们所不希望看到的.下面研究对食饵的收获率q1与捕食者收获率q2在满足什么条件时,系统(3)就没有极限环或者存在极限环.

6.1 极限环不存在

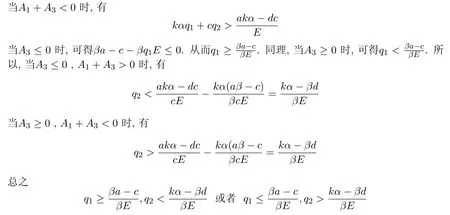
系统(3)是没有极限环的,即当对食饵的收获率q1与捕食者收获率q2满足以上条件时,系统(3)是没有极限环的,从而食饵与捕食者达不到振荡平衡状态.

6.2 极限环存在

现在讨论如何控制对食饵的收获率q1与捕食者收获率q2,使得系统(3)至少存在一个稳定的极限环.以下都是假设在定理3的条件1)成立下讨论.

由A2+2A3+3A4+4A5=0可得−A2=2A3+3A4+4A5.将此项代入−A2+9A4+32A5后可得

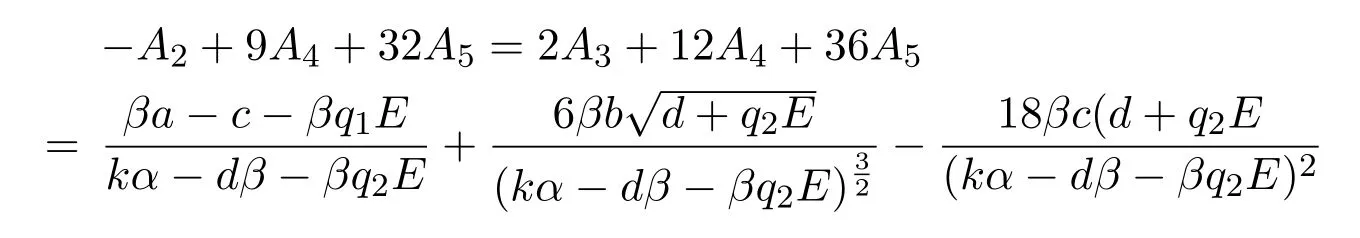
当q2保持不变,q1增大时,由−A2+9A4+32A5的表达式可知,−A2+9A4+32A5逐渐减小,又因为q1−→+∞时,−A2+9A4+32A5−→−∞,所以−A2+9A4+32A5可充分接近0.所以此时在对捕食者的收获率q2保持不变,增大对食饵的收获率q1时,可使系统(3)至少存在一个稳定的极限环,从而食饵与捕食者逐渐达到振荡平衡状态.

[1]刘宣亮.具有收获率和第二类功能性反应的捕食系统可以至少存在两个极限环[J].生物数学学报,1994,9(5):192-199.

[2]聂益民.一类食饵种群具有收获率的HollingII类功能反应生态系统的定性分析[J].陕西师范大学学报, 2001,29(1):2-5．

[3]刘美娟,沈伯骞.捕食者种群具有密度制约的一类厌食系统[J].纯粹数学与应用数学,1999,15(2):7-13.

[4]蔡燧林,张平光.方程的中心焦点判定[J].应用数学学报,1993,16(1):107-113.

[5]叶彦谦.极限环论[M].上海:上海科学技术出版社,1984.

[6]张锦炎.常微分方程几何理论与分支问题[M].北京:北京大学出版社,1987.

A qualitative analysis of a kind of food-predator systemes with HollingII functional resonse and harvesting rates

HE De-ming1,DOU Ji-hong2,HE Wan-sheng1

(1.School of Mathematics and Statistics Institute,Tianshui Normal University,Tianshui741000,China; 2.Department of Mathematics,Northwest University,Xi’an710069,China)

For a class of two kinds of groups have harvested the rate of functional response with HollingII Prey-predator system for qualitative analysis,using ordinary differential equations characterization,stability and bifurcation theory,to be such a biological predator-prey system behavior of the equilibrium point and limit cycle The existence of non-existent conditions and the conclusions of research and development to complement and improve the results of their predecessors.

weak focus,limit,existence

O175

A

1008-5513(2009)04-0752-08

2008-06-10.

甘肃省教育厅科研项目(0608-04),天水师范学院中青年教师科研资助项目(TSA0932).

何德明(1974-),硕士,研究方向：常微分方程定性与稳定性理论.

2000MSC:34C05