Modeling and Kinetic Study on Absorption of CO2 by Aqueous Solutions of N-methyldiethanolamine in a Modified Wetted Wall Column*

Qian Zhi (钱智) and Guo Kai (郭锴)



Modeling and Kinetic Study on Absorption of CO2by Aqueous Solutions of-methyldiethanolamine in a Modified Wetted Wall Column*

Qian Zhi (钱智) and Guo Kai (郭锴)**

Research Center of the Ministry of Education for High Gravity Engineering and Technology, Beijing University of Chemical Technology, Beijing 100029, China

To get more accurate kinetic data of the absorption of CO2into aqueous solution of-methyldiethanolamine, a wetted wall column was modified to more uniformly distribute the liquid on the column surface and gas in the absorbing chamber and change the length of the column. The average liquid film thickness and the liquid-phase mass transfer coefficient were measured, and a correlation for the Sherwood number, Reynolds number and Schmidt number was obtained for the modified wetted wall column. The equilibrium concentrations in chemical reactions were calculated with a minor absolute error for calculating the rate constant more accurately. A mathematical model for the CO2absorption was established based on the diffusional mass transfer accompanied with parallel reversible reactions, and the partial differential equation was solved by Laplace transform. An analytical expression for the concentration of carbon dioxide as a function of time and penetration depth in liquid film and the average interphase mass transfer rate was obtained. This model was also used to calculate the rate constant for a second-order reaction, which was in good agreement with reported data.

absorption, carbon dioxide,-methyldiethanolamine, kinetics, mass transfer

1 Introduction

The removal of carbon dioxide (CO2) and hydrogen sulphide (H2S) from natural and refinery gases is frequently accomplished by using aqueous alkanolamine solutions. Among the alkanolamines,-methyldiethanolamine (MDEA) is widely used as an absorption solvent for acid gases because of its higher H2S selectivity, larger absorption capacity, lower regeneration energy, less hot-degradation and littler corrosion. Since the rate of reaction of MDEA with H2S is instantaneous and the rate of reaction of this alkanolamine with CO2is finite, the selectivity of H2S is controlled by the rate of reaction of the amines with CO2[1]. Gas treatment using alkanolamines has been practiced in industry for over a half century, but it is only recently that substantial progress has been made to understand the processes.

Many studies have been performed on the kinetics of the reaction of CO2with aqueous MDEA solutions [1-9]. However, there are still some discrepancies in the literature on the interpretation of the kinetic data. Some of the discrepancies may come from the differences in the absorbers used, reaction mechanism or the model for absorption process.

The purpose of this study is to present an improved approach for calculating the kinetic data more accurately. A modified wetted-wall column is developed and used to determine the liquid film thickness, liquid-phase mass transfer coefficient and absorption rate. The reaction is assumed as a fast reversible reaction of CO2and OH－in parallel with another rapid pseudo-first-order reversible reaction between CO2and MDEA. A rigorous dynamic-state model is adopted. The mathematical model is solved for the concentration of carbon dioxide as a function of time and penetration depth in liquid film, and then a kinetic equation for this reactive absorption is to be obtained. The dichotomy is employed to solve the equilibrium equations for calculating the equilibrium concentration more accurately.

2 Modified wetted wall column and experiments

2.1 The modified wetted wall column

The distribution of liquid and gas plays an important role in gas-liquid reaction. In this work, a wetted wall column is modified to improve the distribution of liquid and gas. The apparatus is similar to the wetted wall units used in many previous studies on CO2-alkanolamine kinetics, such as those in literature [8, 10-12]. In this work, the conventional design is modified as follows.

a) Instead of entering into the absorption chamberdirectly, the gas flows through an annular porous metaltray with aperture of 20mm at the bottom of the column. The tray produces a pressure difference because of the resistance at the gas inlet, which is helpful to distribute the gas more uniformly in the absorption chamber.

b) Instead of passing a conventional liquid distributor, the liquid is distributed by overflowing on a vertically polished absorption column to avoid channeling and crossing streams, so that the liquid is distributed uniformly.

c) The absorption column is located in the center of two homocentric glass tubes and the water circulates between the tubes to keep the absorption temperature constant. The liquid distribution on the absorption column can be easily observed through the transparent glass.

d) The absorption column is fixed over a socket, so that the length of the column can be adjusted to meet the requirements of the experiment.

Figure 1 depicts the main features of the modified wetted wall column. The column consists of a stainless steel tube inserted by a solid cylinder, forming a uniform annular gap of 1 mm. The outer surface of the tube is 108 mm in height and 25 mm in diameter. The tube is fixed on a socket, so that the column height can be varied between 20 and 200 mm.

Figure 1 The modified wetted wall column 1—absorption column (SS 316); 2—porous metal tray (SS 316); 3—inner cylinder (Pyrex glass); 4—out cylinder(Pyrex glass); 5—threaded rod (carbon steel); 6—top flange (SS 316); 7—bottom flange (SS 316); 8—resistance socket (SS 316); 9—steadier (SS 316)

The gas-liquid contact region is enclosed by a 59 mm ID Pyrex glass tube, which is separated from the circulating water with the same temperature as absorption chamber. The outermost region of the column accommodates the circulating bath of water in an 84 mm OD Pyrex glass annulus. The glass permits the observation of liquid film during the experiment, which should be distributed uniformly and no surface rippling occurs. Two stainless steel flanges, the upper one in 16 mm thickness and 150 mm diameter and the bottom one in 58 mm thickness and 150 mm diameter, and Teflon O-rings provide the seal on both ends of the absorption chamber. The top flange is pressed on the glass cylinders by means of four equally spaced bolts with 14 mm diameter attached to the bottom flange.

The solution passes through the annular gap inside of the column, and overflows on the outer surface of the column (see Fig. 1). The liquid flows as a uniform liquid film on the surface and is collected by the annular draining tunnel at the bottom of the column. The liquid level in the draining tunnel is maintained by controlling the discharge velocity. The gas enters the absorption chamber through an annular porous metal tray with aperture of 20mm, and contacts the liquid counter-currently.

2.2 Experimental procedure

As shown in Fig. 2, the MDEA solution was from the overhead tank, through the rotameter and into a coil submerged in a thermostat. After heated, the chemical solvent entered the absorption column. Having contacted with the gas stream, the solvent was sampled for analysis and then discharged to a liquid saver for recovery at the bottom of the column. The CO2loading of the amine solution was determined by standard titration and conversion methods.

The gas from the cylinder passed the gas rotameter through a surge flask to ensure a stable gas flow. Then the gas was saturated with water by bubbling through the water in the heating tank. After absorption, the gas flowed up to the gas outlet and its flow rate was measured by a soap-film meter. The absorption rate of CO2was determined from the product of the liquid flow rate and the difference in CO2flow rate at the inlet and outlet.

All experiments were carried out under atmospheric pressure and with pure CO2. The temperature was maintained constant to within±0.2K. The MDEA was a commercial product from Jiangsu province, China, with a purity of 99.2% (by mass). The aqueous solutions of MDEA were prepared by distilled-deionized water and the concentration of MDEA was determined by titration with HCl.

Figure 2 Experimental setup

3 THEORY

3.1 Equilibrium reaction of CO2 in aqueous MDEA solutions

When CO2is absorbed into an aqueous solution of MDEA (R3N), several equilibrium reactions occur in the solution, which are as follows:

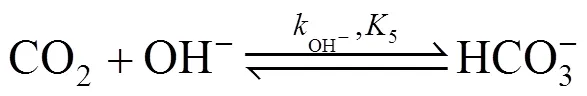
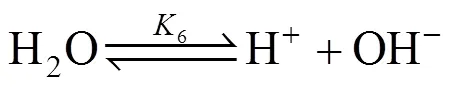
MDEA is easily protonized and the corresponding reaction in the solution is expressed by Eq. (2).

3.2 Reaction mechanism

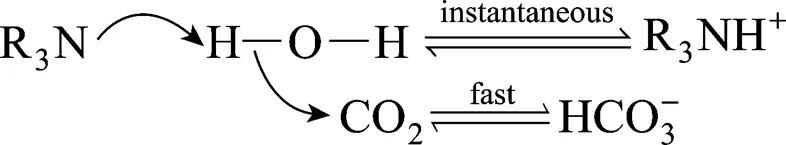
Among the reactions, Eq. (5) is the rate-limiting step, which is independent of and in parallel with the main reaction that follows the zwitterion mechanism,

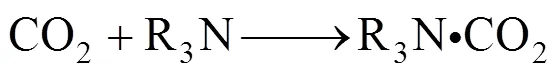
Combining Eqs. (8) and (9), we have Eq. (1).

3.3 Modeling of CO2 absorption in aqueous MDEA solutions

Among the six reactions (1)-(6), reactions (1), (3) and (5) have influence on the absorption of carbon dioxide. However, it is well known that the rate of reaction (3) is very slow and may usually be neglected.

For the absorption of CO2in MDEA aqueous solutions, the overall reaction rate of CO2can be expressed in term of reversible reactions and we have the generally accepted expression:

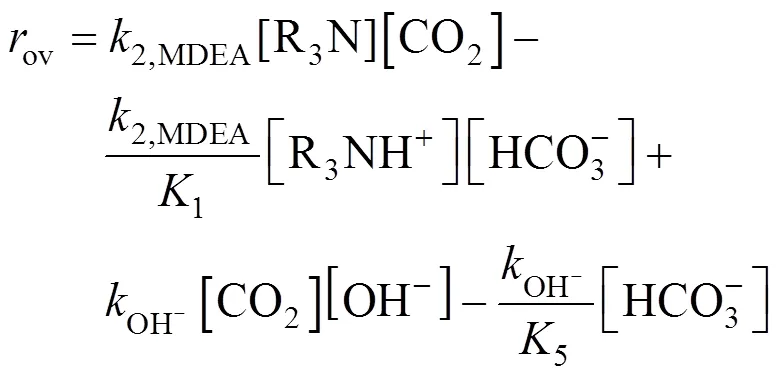
The reaction rate for a reverse reaction can be evaluated by considering the equilibrium condition and the net forward rate of reaction can be deduced from Eq. (10).

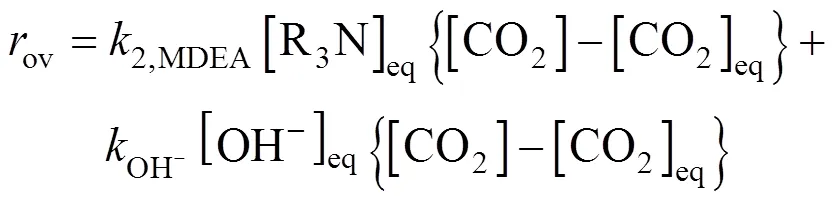
The overall reaction rate constantovhas the following expression

The apparent reaction rate constantappis defined as

The partial differential equation describing the diffusion of CO2into a liquid film accompanied by a pseudo-first-order reversible chemical reaction is

The solution to Eq. (16) is

Using Laplace inverse transform with shifting theorem and replacing the variables to Eq. (17), we obtain an analytical expression for the concentration distribution of carbon dioxide as a function of time and penetration depth in liquid film.

where erfc() is the excess error function. The interphase mass transfer rate is calculated from the first Fick law.

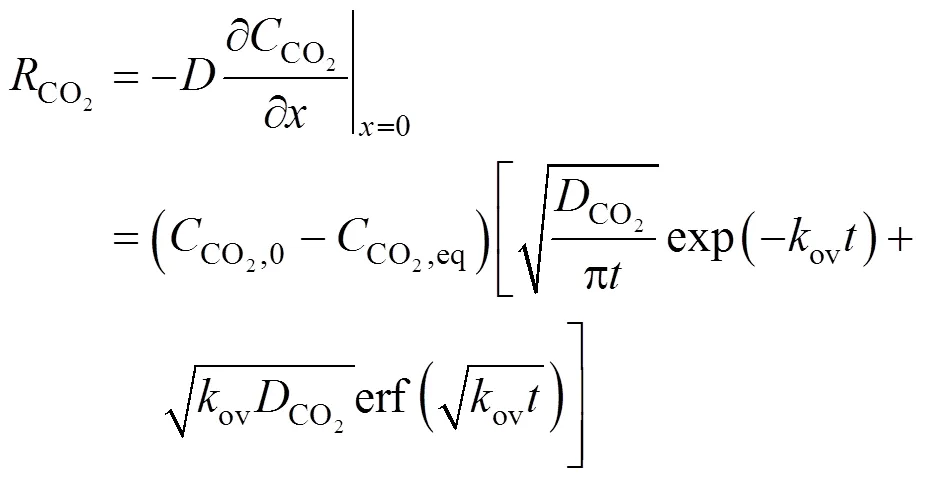
where erf() is the error function. For the smooth liquid film with constant contact time on the wetted wall column, we can define the Higbie age distribution function of mass transfer in the liquid film as

wherecis the contact time. It is well known from the hydrodynamics for wetted wall columns that

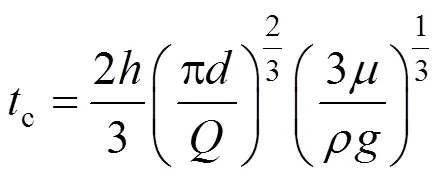
With Eqs. (19) and (20), we have the expression for the average interphase mass transfer rate

To obtain the value ofov, we have to solve Eq. (22) using dichotomy, in which the parameters are acquired from experimental data, physical and chemical properties, and the solution of equilibrium equations.

3.4 Equilibrium model for bulk liquid

In order to solve Eqs. (11), (12), (13) and (22), the equilibrium concentrations of all chemical species, namely, the bulk concentrations, are needed, which can be obtained from the initial concentration of MDEA, the CO2loading of the aqueous MDEA solution and the assumption that all reactions are at equilibrium.

The overall balance for MDEA is

The charge balance is

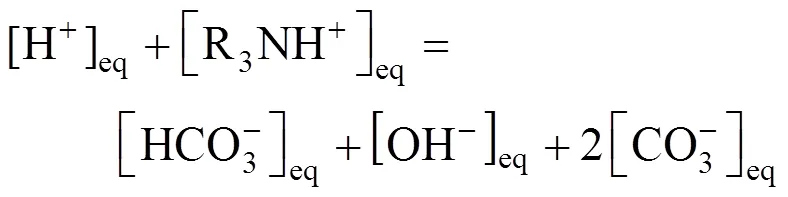
In the reaction scheme (2)-(6), four equilibrium constants,2,3,4and6, are independent. The other can be obtained by an appropriate combination of these independent equilibrium constants. The equilibrium constants of reaction (2)-(4) and (6) are as follows,

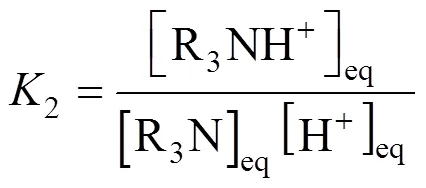
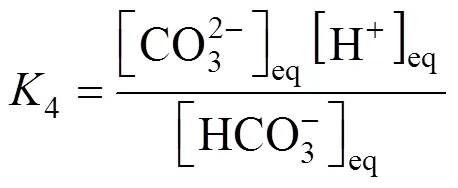
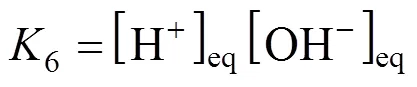
For convenience, the concentrations of chemical species are renamed as follows:

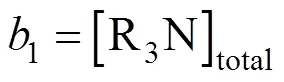
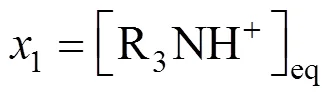
An implicit function for7was obtained by solving Eqs. (23)-(29),

3.5 Properties

In order to interpret the kinetic model and obtain the reaction rate constants, the densities and viscosities of the MDEA solution, Henry’s constants and diffusion coefficient of CO2in the aqueous MDEA solution are needed. These properties are well known and have been determined [6, 15-19], as presented in Table 1.

Table 1 Physical properties of CO2/MDEA system

Table 2 Equilibrium data calculated using dichotomy

4 Results and discussion

All the experiments were conducted in the mass concentration range from 10% to 30% MDEA without the initial CO2loading, at 300 (room temperature), 303, 308 and 313 K under atmospheric pressure.

4.1 Liquid film thickness on column surface

Overflowing is an effective way to distribute the liquid uniformly on the surface of column. Furthermore, as shown in Fig. 3, the column surface was polished to avoid channeling and crossing streams.

Figure 3 Absorbing column without (left) and with (right) liquid film

With the correlation for experimental data, the average liquid film thickness is calculated by

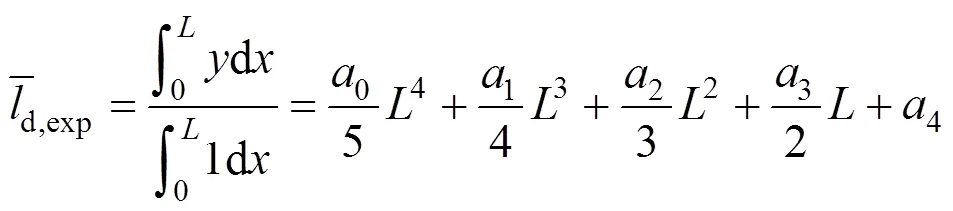
In addition, the average liquid film thickness can be calculated theoretically as follows.

The values of the average film thickness calculated by Eqs. (32) and (33) are listed in Table 3, with an average relative deviation of 4.6%. The results indicate that the MDEA solution is uniformly distributed on the column surface and these values can be used for further correlation. Moreover, the interfacial area can be calculated with the mean liquid film thickness and the kinetic data can be obtained more accurately.

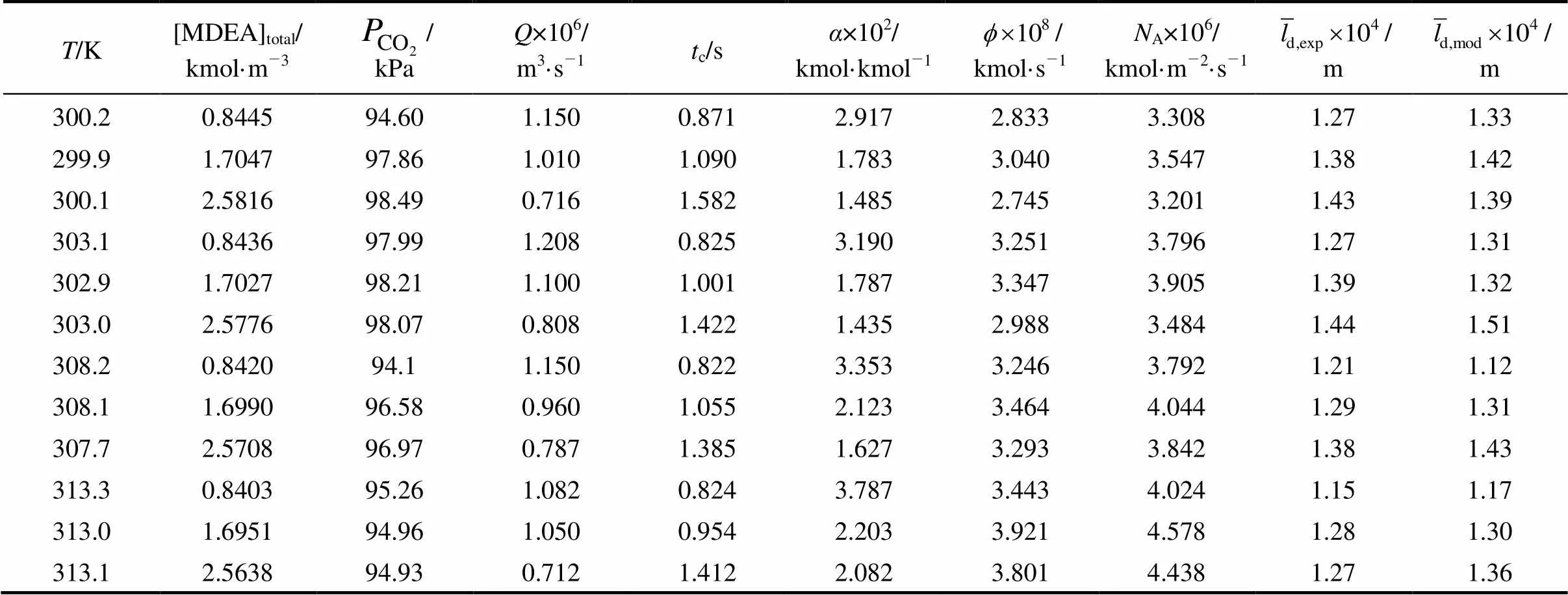
Table 3 Experimental data for the absorption of CO2 in initially unloaded aqueous solutions of MDEA

Table 4 The reaction rate constants and liquid film mass transfer coefficient

4.2 Liquid film mass transfer coefficient

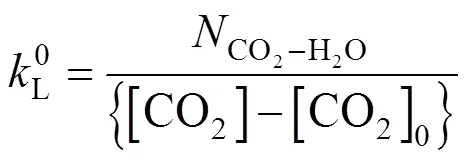
where the subscript 0 indicates condition in the bulk.

Figure 4 Comparison of liquid-phase mass transfer coefficient between calculated and experimental data

4.3 CO2 absorption in aqueous MDEA solutions

Figure 5 Concentration profile of CO2as a function of time and penetration depth in liquid film for absorption of CO2in 10% MDEA solution at 300 K

A comparison of the second-order rate constant2,MDEAfrom this study with the literature values is shown in Fig. 6, indicating that the apparatus and model developed in this work can be used to obtain2,MDEA. The temperature dependence of the rate constants is fitted by the Arrhenius equation

whereis in K, and2,MDEAis in m3·kmol－1·s－1. The activation energy determined from Eq. (36) is 43.15 kJ·mol－1, which can be compared with the reported values of 71.5 kJ·mol－1[2], 42.4 kJ·mol－1[1], 42.7 kJ·mol－1[3], 48.0 kJ·mol－1[4], 47.9 kJ·mol－1[5], 38.07 kJ·mol－1[6], 45.4 kJ·mol－1[7], 44.9 kJ·mol－1[8], and 48.2 kJ·mol－1[9].

5 Conclusions

A mathematical model based on the equilibrium of fast reversible reactions is developed. The calculated kinetic parameters are in good agreement with literature values, so that the model is satisfactory to represent CO2absorption rates. The modified experimental apparatus and the mathematical method provide a useful template to our further studies on the absorption with fast reactions.

NOMENCLATURE

diffusivity of a gas in liquid, m2·s－1

gravitational constant, m·s－2

solubility of gas in solution, kPa·m3·kmol－1

height of absorbing column measured from the top, m

equilibrium constant

appapparent reaction rate constant, s－1

ovoverall pseudo first order reaction rate constant, s－1

2,MDEAsecond-order reaction rate constant, m3·kmol－1·s－1

total length of absorbing column, m

dliquid film thickness, m

volumetric flow rate of liquid, m3·s－1

radius of tube, m

reaction rate, kmol·m－3·s－1

LSherwood number

temperature, K

ccontact time, s

mliquid flow rate, kg·m－1

loading of CO2in amine, kmol·kmol－1

viscosity, Pa·s

density, kg·m－3

Superscripts

0 pure carbon dioxide-water system

Subscripts

eq equilibrium state

exp experimental value

L liquid phase

mod model calculation value

1 Versteeg, G.F., van Swaaij, W.P.M., “On the kinetics between CO2and alkanolamines both in aqueous and non-aqueous solutions-II. Tertiary amines”,..., 43 (3), 587-591 (1988).

2 Haimour, N., Bidarian, A., Sandall, O.C., “Kinetics of the reaction between carbon dioxide and methyldiethanolamine”,..., 42 (6), 1393-1398 (1987).

3 Tomcej, R., Otto, F., “Absorption of CO2and N2O into aqueous solutions of methyldiethanolamine”,., 35 (5), 861-864 (1989).

4 Littel, R.J., van Swaaij, W.P.M., Versteeg, G.F., “Kinetics of carbon dioxide with tertiary amines in aqueous solution”,., 36 (11), 1633-1640 (1990).

5 Rangwala, H.A., Morrell, B.R., Mather, A.E., Otto, F.D., “Absorption of CO2into aqueous tertiary amine/MEA solutions”,...., 70 (3), 482-490 (1992).

6 Rinker, E.B., Ashour, S.S., Sandall, O.C., “Kinetics and modeling of carbon dioxide absorption into aqueous solutions of-methyldiethanolamine”,..., 50 (5), 755-768 (1995).

7 Pani, F., Gaunand, A., Cadours, R., Bouallou, C., Richon, D., “Kinetics of absorption of CO2in concentrated aqueous methyldiethanolamine solutions in the range 296 K to 343 K”,..., 42 (2), 353-359 (1997).

8 Ko, J.J., Li, M.H., “Kinetics of absorption of carbon dioxide into solutions of-methyldiethanolamine+water”,..., 55, 4139-4147 (2000).

9 Jamal, A., Meisen, A., Lim, C.J., “Kinetics of carbon dioxide absorption and desorption in aqueous alkanolamine solutions using a novel hemispherical contactor—II. Experimental results and parameter estimation”,..., 61, 6590-6603 (2006).

10 Blanc, C., Demarais, G., “Reaction rate of CO2with diethanolamine”,..., 24, 43-52 (1984).

11 Saha, A.K., Bandyopadhyay, S.S., Biswas A.K., “Kinetics of absorption of CO2into aqueous solutions of 2-amino-2-methyl-1-propanol”,..., 50 (22), 3587-3598 (1995).

12 Mandal, B., Bandyopadhyay, S.S., “Simultaneous absorption of CO2and H2S into aqueous blends of-methyldiethanolamine and diethanolamine”,..., 40, 6076-6084 (2006).

13 Donaldson, T.L., Nguyen, Y.N., “Carbon dioxide reaction kinetics and transport in aqueous amine membranes”,...., 19, 260-266 (1980).

14 Yu, W.C., Astarita, G., Savage, D.W., “Kinetics of carbon dioxide absorption in solutions of methyldiethanolamine”,..., 40, 1585-1590 (1985).

15 Haimour, N., Sandall, O.C., “Absorption of carbon dioxide into aqueous methyldiethanolamine”,..., 39 (12), 1791-1796 (1984).

16 Versteeg, G.F., van Swaaij, W.P.M., “Solubility and diffusivity of acid gases (CO2, N2O) in aqueous alkanolamine solutions”,..., 33 (1), 29-34 (1988).

17 Al-Ghawas, H.A., Hagewiesche, D.P., Ruiz-Ibanez, G., Sandall, O.C., “Physicochemical properties important for carbon dioxide absorption in aqueous methyldiethanolamine”,..., 34 (4), 385-391 (1989).

18 Xu, S., Otto, F.D., Mather, A.E., “Physical properties of aqueous AMP solutions”,..., 36 (1), 71-75 (1991).

19 Saha, A.K., Bandyopadhyay, S.S. and Biswas, A.K., “Solubility and diffusivity of N2O and CO2in aqueous solutions of 2-amino-2- methyl-1-propanol”,..., 38 (1), 78-82 (1993).

20 Zhang, X., Zhang, C.F., Liu, Y., “Kinetics of absorption of CO2into aqueous solution of MDEA blended with DEA”,...., 41, 1135-1141 (2002).

2008-12-10,

2009-04-17.

China Petroleum & Chemical Corporation (105044).

** To whom correspondence should be addressed. E-mail: guok@mail.buct.edu.cn