An Unsteady Heterogeneous Mass Transfer Model for Gas Absorption Enhanced by Dispersed Third Phase Droplets*

SHEN Shuhua (沈树华), MA Youguang (马友光), LU Sumin (卢素敏) and ZHU Chunying (朱春英)



An Unsteady Heterogeneous Mass Transfer Model for Gas Absorption Enhanced by Dispersed Third Phase Droplets*

SHEN Shuhua (沈树华), MA Youguang (马友光)**, LU Sumin (卢素敏) and ZHU Chunying (朱春英)

School of Chemical Engineering and Technology, State Key Laboratory of Chemical Engineering, Tianjin University, Tianjin 300072, China

A model for one-dimensional unsteady heterogeneous mass transfer was developed based on Danckwerts’ surface renewal theory in order to describe the mass transfer enhancement of absorption process for a slightly soluble gas in a gas-liquid-liquid system. The model accounts for the mass transfer resistance within the dispersed phase and the effect of emulsion viscosity on mass transfer. An analytical solution for enhancement factor was obtained by Laplace domain transformation. The absorption rates of carbon dioxide in the dodecane-in-water and castor oil-in-water systems were measured in a thermostatic reactor, and the enhancement factors were calculated at different volume fractions of dispersed phase and stirrer speeds. The model predictions agree well with the experimental data.

enhancement factor, mass transfer, absorption, gas-liquid-liquid

1 INTRODUCTION

Mass transfer in gas-liquid-liquid system is of increasing interest due to its widely application in bioprocess industry and homogeneous catalysis systems [1]. Experiments have shown that the gas-liquid mass transfer rate can be enhanced by adding a dispersed liquid phase in which gas is more soluble than in the continuous phase [2-5]. The mechanism of the enhancement was mostly explained by the “shuttle effect” [6, 7], in which the dispersed droplets were supposed to transfer an additional amount of gas to the liquid bulk through the adsorption in the gas-liquid diffusion layer and desorption in the bulk, consequently, resulting in an enhanced concentration gradient of the gas solute near the interface.

Many theoretical models were developed for describing the effect of the dispersed phase droplets on gas absorption enhancement and could be mainly classified as “stationary” or “instationary” and “pseudo-homogeneous” or “heterogeneous” models, which could be further subdivided as 1-D, 2-D and 3-D models [8-12]. The advantages of the homogeneous models are their numerical simplicity and shorter computation time. Although these models can predict the changing trend of the enhancement factor with operation conditions, such as gas-liquid contact time and relative solubility, some of the assumptions are obviously unreasonable. For example, the mass transfer resistance within the dispersed phase is neglected, this may be suitable for solid particles with high diffusion coefficients, but for droplets, it will bring about marked deviation due to the relatively lower diffusion coefficients. Heterogeneous mass transfer models consider the local geometry of the dispersed phase near the gas-liquid interface, the mass transfer resistance within the dispersed phase., so that it is more rational to describe the gas absorption, especially from 2-D or 3-D perspectives. Unfortunately, the computation is much more complex and it is usually difficult to attain an analytical solution.

In the present wok, the effects of dispersed dodecane and castor oil on carbon dioxide absorption are investigated experimentally. A model for one-dimensional unsteady heterogeneous mass transfer is developed based on Danckwerts’ surface renewal theory by considering the mass transfer resistance within the dispersed phase and the effect of emulsion viscosity. The model is solved analytically by Laplace domain transformation [13].

2 EXPERIMENTAL

The experiments were carried out in a thermostatic reactor [(298.15±0.1)K] for CO2(>99.5% mass fraction) absorption in dodecane-in-water emulsions [consisted of dodecane in water stabilized by 0.4% (volume fraction) Tween 20] and castor oil-in-water emulsions [consisted of castor oil in water stabilized by 3% (volume fraction) Tween 20]. The initial absorption pressure was 2.0265×105Pa. As shown in Fig. 1, two stirrers were located centrally in the gas phase and the liquid phase for mixing uniformity. Four stainless steel baffles were mounted symmetrically to prevent tangential flows and increase the mixing effectiveness. A pressure difference transmitter was connected with the computer for real-time automatic data collection. Before each experiment, the emulsion was degassed by sparging nitrogen and renewed by carbon dioxide; the reactor was washed with acetone then distilled water.

Figure 1 Schematic set-up of the absorption in stainless stirred tank 1—N2inlet valve; 2—CO2inlet valve; 3—balance tank; 4—junction valve; 5—pressure difference transmitter connected with the computer; 6—gas outlet valve

Tween 20, dodecane (viscosity 1.93×10－3Pa·s) and castor oil (viscosity 0.715 Pa·s) were purchased from Tianjin Kermel Chemical Reagent Co., Ltd. For all the emulsion fractions applied, the mean droplets size (p) of dodecane and castor oil are 4×10－6m (1.0×10－6-1.0×10－5m) and 1.7×10－5m (1.0×10－6-1.0×10－4m), respectively, measured by Mastersizer S (Malvern Instruments Ltd, UK). The viscosities of dodecane- in-water and castor oil-in-water emulsions were measured by the DV-III Ultra Programmable Rheometer (Brookfield Engineering Laboratories, Inc., USA). As shown in Figs. 2 and 3, the relative viscosity of emulsion to pure water can be expressed as a function of the volume fraction of dispersed phase as follows.

Dodecane-water:

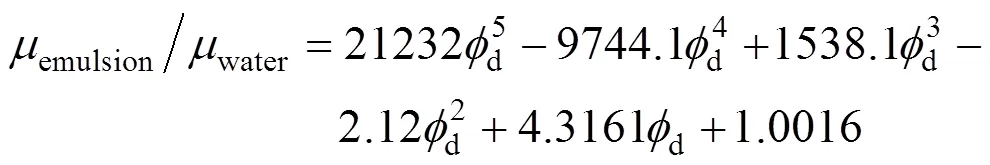
Castor oil-water:

Figure 2 Effect of dodecane volume fraction on relative viscosity of emulsion to pure water▲ experimental data; —— fitting curve

The relative diffusion coefficients of carbon dioxide in dodecane and castor oil to pure water are 1.28 and 0.0058 respectively by Wilke-Chang Equation [14]. The distribution coefficient of carbon dioxide in dodecane and pure water was 1.93 calculated by the data in Ref. [15]. Lacking of the solubility of carbon dioxide in castor oil in the literature, the distribution coefficient of carbon dioxide in castor oil and pure water was measured as 1.73.

Figure 3 Effect of castor oil volume fraction on relative viscosity of emulsion to pure water▲ experimental data; —— fitting curve

3 THEORETICAL MODEL

3.1 Assumptions

As shown in Fig.4, we make following assumptions for modeling of gas absorption enhanced by dispersed phase droplets.

(1) The gas-liquid interface in the reactor is planar in the range of stirrer speeds applied.

(2) The dispersed phase droplets are small so that they are accommodated in the mass transfer region and are cubic ones with identical volumes [10].

(3) There is no contact between the gas and the dispersed phase.

(4) The thickness of the continuous phase layer near the gas-liquid interface (1) isp/4 [13, 16].

(5) The distribution of the dispersed droplets near the gas-liquid interface is the same as that in the bulk phase [11].

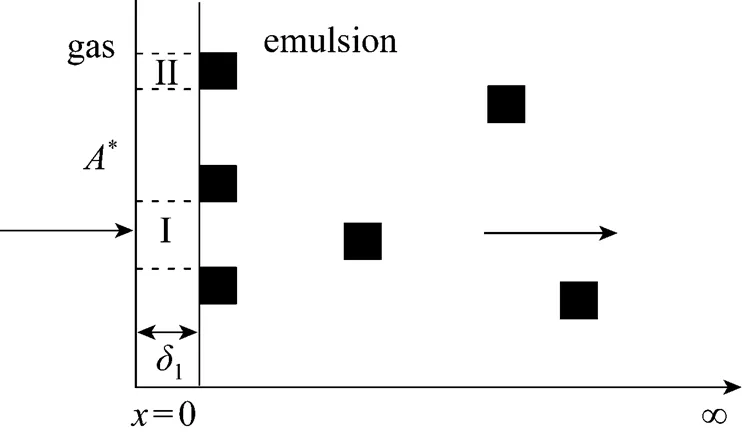
Figure 4 Sketch of mass transfer in a surface element

(6) The effect of the droplets adhering to the gas-liquid interface on mass transfer rate is dominating, and the effect of droplets next to them is negligible.

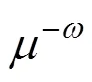
3.2 Governing equations and solutions

For the convenience of calculation, the continuous phase close to the gas-liquid interface is divided into two regions: without droplets adhering (region I) and with droplets adhering (region II), as shown in Fig. 4.

For the continuous phase in region I, the differential mass balance equation is

The initial and boundary conditions are:

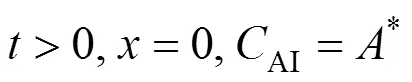
where

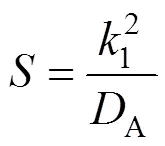
For the continuous phase in region II, the differential mass balance equation is

with the following conditions:

For the dispersed droplets adhering to the gas-liquid interface, the differential mass balance equation is

The initial and boundary conditions are:

Equations (11) and (12), transformed into the Laplace domain (), yield the following solution

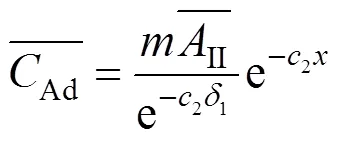
where

With Eqs. (10) and (13), Eq.(15) gives:

For the continuous phase near the gas-liquid interface,the overall solute concentrationOcan be fitted as:

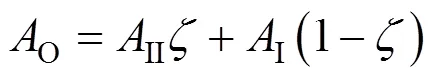
where

andis the volume fraction of the droplets near the gas- liquid interface. Based on assumption (5),is given as:

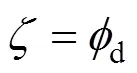
For the continuous phase near the gas-liquid interface, the overall differential mass balance equation is

with the following conditions:

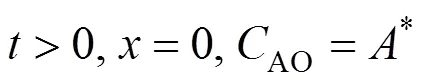
With the surface renewal theory [13], the absorption rate with the dispersed phase,emulsion, can be described as

The absorption rate in pure waterwateris

3.3 Enhancement factor

The enhancement factor based on “shuttle effect” is defined as

Substitution of Eqs. (16), (19), (23), (24) and (25) into Eq. (26) gives

where

To our knowledge, the influence of emulsion viscosity on mass transfer was seldom considered in the literature. Evidently, the emulsion viscosity affects the hydrodynamic behavior of the system, increasing the gas-liquid contact time and decreasing the diffusion coefficient [17, 18]. According to assumption (7), the relative mass transfer coefficient of the emulsion system to the pure water can be described as

Combining Eqs. (27) and (29), we obtain the overall enhancement factor

wherelis calculated according to Ref. [19].

4 RESULTS AND DISCUSSION

The models proposed in the literature are mostly solved numerically and usually contain many unknown parameters, so that the precise and rapid prediction of enhancement factors is considerably difficult. It is always desirable to have an analytical solution for both theoretical study and practical applications.

In this work, the model proposed was solved analytically by Laplace domain transformation, and especially, the mass transfer resistance within the dispersed phase and the effect of emulsion viscosity on mass transfer were taken into account. Only one parameterneeds to be determined for calculating the enhancement factor.

4.1 Effect of dispersed phase on gas absorption

Table 1 Model parameter ω at different stirrer speeds

4.2 Effect of emulsion viscosity on enhancement factor

The comparison of predicted values of enhancement factor between the two models shows that the model taking into account the influence of emulsion viscosity on mass transfer is more accurate, as shown in Figs. 5 and 6. The effect of emulsion viscosity on enhancement factor is significant and should not be neglected. However,decreases as the stirring intensity increases, so that its influence on enhancement factor decreases accordingly. It could be ascribed to the collision of droplets to the boundary layer in higher agitation intensity, resulting in higher surface renewal frequency, hence, the negative effect of emulsion viscosity on mass transfer becomes inconspicuous even negligible.

Based on the discussion above, the enhancement of gas absorption with the dispersed phase is due to the enhanced solute concentration gradient near the interface. In addition, the effect of emulsion viscosity on mass transfer coefficient should be considered for better prediction of the enhancement factors.

5 CONCLUSIONS

(1) A model for one-dimensional unsteady heterogeneous mass transfer was developed considering the mass transfer resistance within the dispersed phase and the effect of emulsion viscosity. An analytical solution for the enhancement factor was obtained by Laplace domain transformation.

NOMENCLATURE

solute concentration in the continuous phase, mol·m－3

*solute concentration at the gas-liquid interface, mol·m－3

Asolute concentration, mol·m－3

diffusion coefficient, m2·s－1

rrelative diffusion coefficient of solute in dispersed phase to pure water

pmean droplets size, m

enhancement factor

absorption rate of gas, mol·m－2·s－1

lmass transfer coefficient, m·s－1

distribution coefficient of solute in dispersed phase and pure water

stirrer speed, s－1

surface renewal frequency, s－1

1thickness of continuous phase close to the gas-liquid interface, m

volume fraction of dispersed phase near the gas-liquid interface

viscosity, Pa·s

influence factor of viscosity on mass transfer coefficient

Superscripts

￣ Laplace transformation

Subscripts

b bulk phase

d dispersed phase

emulsion emulsion system

O overall

OE overall enhancement factor

SE enhancement factor based on “shuttle effect”

water water system

I continuous phase in region I

II continuous phase in region II

1 Dumont, E., Delmas, H., “Mass transfer enhancement of gas absorption in oil-in-water systems: A review”,..., 42 (6), 419-438 (2003).

2 Bruining, W.J., Joosten, G.E.H., Beenackers, A.A.C.M., Hofman, H., “Enhancement of gas-liquid mass transfer by a dispersed second liquid phase”,..., 41 (7), 1873-1877 (1986).

3 Littel, R.J., Versteeg, G.F.A., van Swaaij, W.P.M., “Physical absorption of CO2and propene into toluene/water emulsions”,., 40 (10), 1629-1638 (1994).

4 van Ede, C.J., van Houten, R., Beenackers, A.A.C.M., “Enhancement of gas to water mass transfer rates by a dispersed organic phase”,..., 50 (18), 2911-2922 (1995).

5 Junker, B.H., Hatton, T.A., Wang, D.I.C., “Oxygen transfer enhancement in aqueous/perfluorocarbon fermention systems: I. Experimental abservation”,.., 35 (6), 578-585 (1990).

6 Kars, R.L., Best, R.J., Drinkenburg, A.A.H., “The sorption of propane in slurries of active carbon in water”,..., 17 (3), 201-210 (1979).

7 Alper, E., Wichtendahl, B., Deckwer, W.D., “Gas absorption mechanism in catalytic slurry reactors”,..., 35 (1/2), 217-222 (1980).

8 Holstvoogd, R.D., van Swaaij, W.P.M., “The influence of adsorption capacity on enhanced gas absorption in activated carbon slurries”,..., 45 (1), 151-162 (1990).

9 Karve, S., Juvekar, V.A., “Gas absorption into slurries containing fine catalyst particles”,..., 45 (3), 587-594 (1990).

10 Nagy, E., “Three-phase mass transfer: One-dimensional heterogeneous model”,..., 50 (5), 827-836 (1995).

11 Lin, C., Zhou, M., Xu, C.J., “Axisymmetrical two-dimensional heterogeneous mass transfer model for the absorption gas into liquid-liquid dispersions”,..., 54 (3), 389-399 (1999).

12 Brilman, D.W.F., Goldschmidt, M.J.V., Versteeg, G.F., van Swaaij, W.P.M., “Heterogeneous mass transfer models for gas absorption in multiphase systems”,..., 55 (15), 2793-2812 (2000).

13 Demmink, J.F., Mehra, A., Beenackers, A.A.C.M., “Gas absorption in the presence of particles showing interfacial affinity: case of the fine sulfur precipitates”,..., 53 (16), 2885-2902 (1998).

14 Wilke, C.R., Chang, P., “Correlation of diffusion coefficients in dilute solutions”,., 1 (2), 264-270 (1955).

15 Walter, H., Edgar, B.W., Philip, S., “Solubility of propane and carbon dioxide in heptane, dodecane, and hexadecane”,...., 17 (1), 59-61 (1972).

16 Vinke, H., Hamersma, P.J., Fortuin, J.M.H., “Enhancement of the gas-absorption rate in agitated slurry reactors by gas-adsorbing particlesadhering to the gas bubbles”,..., 48 (12), 2197-2210 (1993).

17 Zhang, J.M., Xu, C.J., Zhou, M., “The mechanism model of gas-liquid mass transfer enhancement by fine catalyst particles”,..., 120 (3), 149-156 (2006).

18 Zhang, G.D., Cai, W.F., Xu, C.J., Zhou, M., “A general enhancement factor model of the physical absorption of gases in multiphase systems”,..., 61 (2), 558-568 (2006).

19 Lekhal, A., Chaudhari, R.V., Wilhelm, A.M., Delmas, H., “Gas-liquid mass transfer in gas-lqiuid-liquid dispersions”,..., 52 (21/22), 4069-4077 (1997).

20 Eckenfelder, W.W., Barnhart, E.L., “The effect of organic substances on the transfer of oxygen from air bubble in water”,., 7 (4), 631-634 (1961).

2008-11-12,

2009-03-11.

the National Natural Science Foundation of China (20176036).

** To whom correspondence should be addressed. E-mail: ygma@tju.edu.cn