Measurement and Correlation of Solid-Liquid Equilibria of Phenyl Salicylate with C4 Alcohols
WEI Dongwei (魏东炜)*, PEI Yanhong (裴艳红), ZHANG Chao (张超) and YAN Feng (闫峰)
Measurement and Correlation of Solid-Liquid Equilibria of Phenyl Salicylate with C4Alcohols
WEI Dongwei (魏东炜)*, PEI Yanhong (裴艳红), ZHANG Chao (张超) and YAN Feng (闫峰)
Tianjin Research and Development Center for Petrochemical Technology, Tianjin University, Tianjin 300072, China
In an equilibrium vessel, the solid-liquid equilibria (SLE) for three binary mixtures of phenyl salicylate with 1-butanol, 2-butanol, and 2-methyl-1-propanol, respectively, have been measured from 283.15 K to the melting temperature of the solute using a method in which an excess amount of solute was equilibrated with the alcohol solution. The liquid concentrations of the investigated phenyl salicylate in the saturated solution were analyzed by UV spectrometry. Activity coefficients for phenyl salicylate have been calculated by means of the Wilson, NRTL, and UNIQUAC equations and with them were correlated solubility data that were compared with the experimental ones. The best correlation of the solubility data has been obtained by the Wilson equation by which the average root-mean-square deviation of temperature for the three systems is 1.03 K.
phenyl salicylate, alcohol, solid-liquid equilibrium, activity coefficient, correlation
1 INTRODUCTION
The chemical structure of phenyl salicylate (C13H10O3), also known as salol or phenyl 2-hydroxybenzoate, involved in this study is shown in Fig. 1.
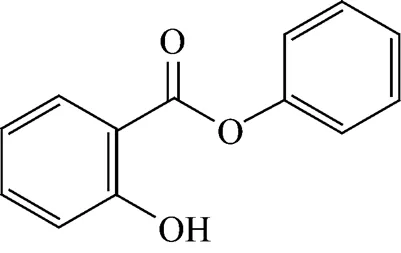
Figure 1 Structure of the phenyl salicylate molecule
Phenyl salicylate, which commonly appears as a white powder with aromatic aroma, has been extensively used in the manufacture of plastics and suntan oils and medicinally as an analgesic or an antipyretic or a coating for pills in which the medicine is intended for controlled release [1, 2]. In industry, phenyl salicylate is crystallized from solution as a final step [3-6]. Hence, crystallization is a key step in many respects, and it determines the yield and quality of the target product. To determine proper solvents and to design an optimized production process, it is necessary to know the solubility of phenyl salicylate in different solvents.
Limited data is available on the solubility and temperature dependence of the solubility of phenyl salicylate. The aim of this article is to report the examination of solid-liquid equilibria (SLE) in binary mixtures of phenyl salicylate with C4alcohols, that is, 1-butanol, 2-butanol, and 2-methyl-1-propanol, from 283.15 K to the melting temperature of phenyl salicylate.
2 EXPERIMENTAL
2.1 Materials
1-Butanol, 2-butanol, and 2-methyl-1-propanol were purchased from Tianjin Kewei Chemical Reagent Co. All above solvents were refluxed over freshly activated CaO for 2 h and then fractionally distilled. Liquids were stored over freshly activated molecular sieves of type 4A. Analysis, using the Karl-Fischer technique, showed that the water content in each of the solvents was less than 0.02% (by mass). The purities of the solvents were determined in our laboratory by gas chromatography, for 1-butanol, 99.98% (by mass), for 2-butanol, 99.95% (by mass), and for 2-methyl-1-propanol, 99.93% (by mass). Phenyl salicylate, obtained from Hangzhou Chiral Medicine Chemicals Co., was purified by recrystallization from ethanol solution two times, followed by sublimation at 310 K under reduced pressure. The obtained sample was kept in a desiccator with dry silica gel. The sample was repurified by sublimation every half a month to use as fresh a sample as possible. The purity of the sample was determined to be 0.9995 in the mole fraction by a differential scanning calorimeter (Mettler DSC30).
2.2 Procedure
The solid-liquid equilibria (SLE) in binary mixtures of phenyl salicylate with alcohols were measured by a static analytical method that was described in our previous work [7], and the brief explanation of this method is given here. The experimental saturated solutions were prepared by excess solute, phenyl salicylate, in glass vessels containing the solvent. Solubilities were determined by equilibrating the solute with solvent in a water jacketed vessel with magnetic stirring in constant temperature water bath (±0.05 K) for at least 3 days, followed by a 6 h settling time. The actual temperature in the glass vessel was monitored using a mercury thermometer with an uncertainty of 0.05 K. The fluid between the internal and external glass tube can be exchanged by pressing or relaxing the gas-bag at the top of glass tube. Portions of phenyl salicylate saturated solutions were transferred by syringe from internal glass tube to volumetric flasks to determine the amounts of samples diluted quantitatively with solvent mixtures using a spectrophotometer (SHIMADZU UV-160A). Syringes (10 ml) and needles were preheated when necessary to prevent nucleation inside the syringes during sampling. The mole fractions of the dilute solutions were determined from absorbanceconcentration calibration curves derived from measured absorbance of solutions of known concentrations.

3 RESULTS AND DISCUSSION
3.1 Experimental results
Table 1 lists the direct experimental results of the SLE, temperature1, the mole fraction of the phenyl salicylate and1, and the experimental activity coefficients in the saturated solution for the investigated liquidus curves. The mole fraction,1, is reported to represent an average of three measurements with reproducibility better than 97%.


Table 1 Experimental solid-liquid equilibrium temperatures, T for {phenyl salicylate (x1)+alcohol(1x1)} systems; γ1, experimental activity coefficient of solute
3.2 Data regression analysis
The solubility of a solid (1) in a liquid can be calculated by Ref. [17]:
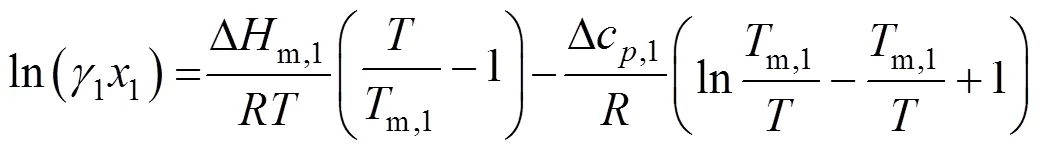
where1is the solubility and1the solute activity coefficient, which needs to be determined. From a model,m,1, Δm,1, and Δc,1, the melting temperature, the molar enthalpy of fusion, and the molar capacity of the solute, respectively.
In this study, three methods are used to derive the solute activity coefficient1from the Wilson, NRTL, and UNIQUAC equations. The exact mathematical forms of the equations for binary systems are presented as follows. All characteristic data are given in Table 2 for the components involved in this study.

Table 2 Characteristic data of pure materials
① Our experimental data. Themvalue has also been determined by Paladi. [8] to 315.15 K, and from Refs. [9] and [2] to 316.15 K, and 314.15-316.15 K, respectively;② Our experimental data determined by differential scanning calorimetry [10]. The Δmvalue has also been determined by Hanaya. [11] to 19.16 kJ·mol-1with a melting temperature of 314.97 K, by Gatta. [12] to 19.18 kJ·mol-1at melting temperature of 314.94 K, by Richert. [13] to 19.35 kJ·mol-1at melting temperature of 315.0 K, and from the database [14] to 19.00 kJ·mol-1with a melting temperature range of 314.15 to 316.15 K;③Ref. [11], at the melting temperature 314.97 K;④ Calculated from Ref. [9], density 1.2614 g·cm-3at 30°C;⑤Ref. [15];⑥ Calculated from UNIFAC tables [16].
Wilson equation [18] The activity coefficient of this equation is given by
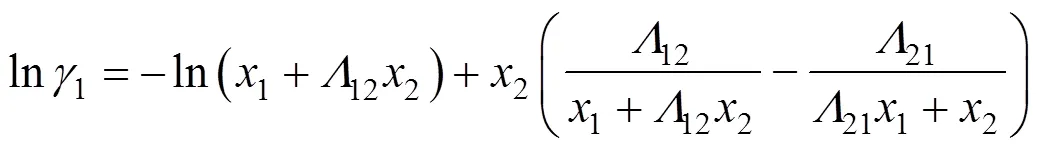
where



NRTL equation [19] The activity coefficient of this equation is given by

where

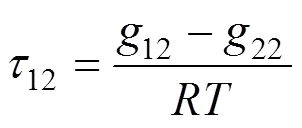

UNIQUAC equation [20] The activity coefficient of this equation is given by

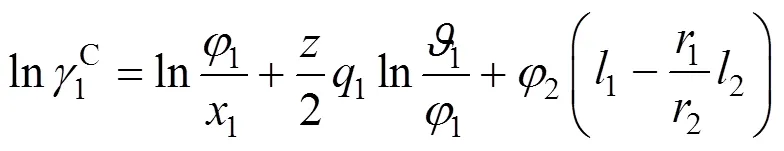

where


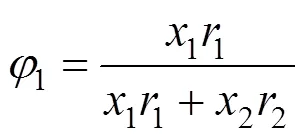
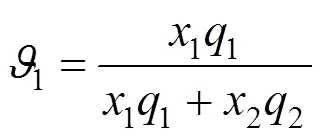

The parameters of the three equations were evaluated by minimizing the following objective function,obj, between the calculated and experimentally determined temperature:

where the summation is over allth data point. The root-mean-square deviation of temperature {(defined by Eq. (15)} was used as a measure of the goodness of the solubility correlation.

whereis the number of experimental points, and 2 the number of adjustable parameters.

4 CONCLUSIONS


Table 3 Correlation of the solubility data of {phenyl salicylate (1) + alcohol (2)} by means of the Wilson, NRTL, and UNIQUAC equations: values of parameters and measures of deviations
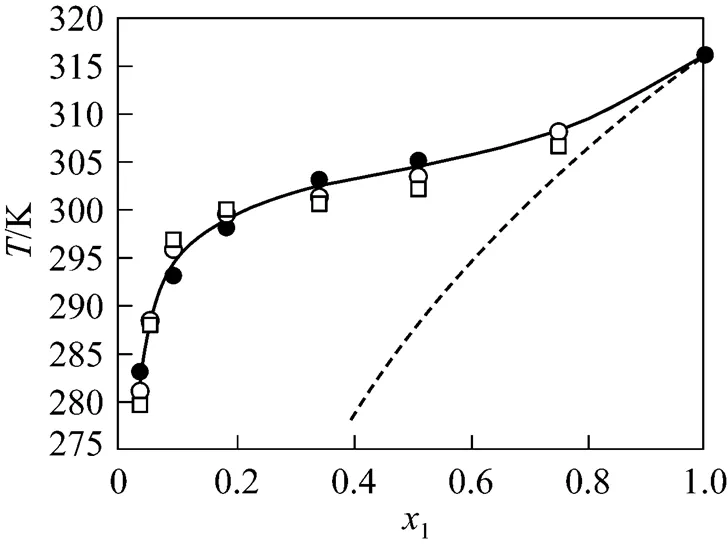
Figure 2 Solubility of phenyl salicylate in 1-butanol
● experimental data;○ calculated by the NRTL equation;
□ calculated by the UNIQUAC equation; solid line is from correlation by the Wilson equation; dotted line designates ideal solubility

Figure 3 Solubility of phenyl salicylate in 2-butanol
● experimental data; ○ calculated by the NRTL equation;
□ calculated by the UNIQUAC equation; solid line is from correlation by the Wilson equation; dotted line designates ideal solubility

Figure 4 Solubility of phenyl salicylate in 2-methyl-1- propanol
● experimental data; ○ calculated by the NRTL equation;
□ calculated by the UNIQUAC equation; solid line is from correlation by the Wilson equation; dotted line designates ideal solubility
NOMENCLATURE
Δpdifference between the heat capacities of the solute in the solid, J·mol-1·k-1
Δmenthalpy of fusion at temperaturem, J·mol-1
number of experimental data
area parameter
volume parameter
temperature, K
mnormal melting temperature, K


molar volume, cm3·mol-1
mole fraction in the solution

12nonrandomness parameter
activity coefficient
standard deviation
Superscripts
C combinatorial
cal calculated value
R residual
Subscripts
1 solute (phenyl salicylate)
2 solvent
1 The Columbia Encyclopedia, 6th edition, Columbia University Press, New York (2007).
2 O’Neil, M.J., “The Merck index: an encyclopedia of chemicals, drugs, and biologicals”, 14th edition, Merck Research Laboratories, Whitehouse Station, N.J. (2006).
3 Kuriakose, G. Nagaraju, N., “Selective synthesis of phenyl salicylate (salol) by esterification reaction over solid acid catalysts”,...-., 223, 155-159 (2004).
4 Shamshuddin, S.Z.M., Nagaraju, N., “Transesterification: salol synthesis over solid acids”,.., 7, 593-599 (2006).
5 Mills, L.E., “Method of making salol and other aryl esters”, US Pat., 1606171 (1926).
6 Dvornikoff, M.N., “Manufacture of salol”, US Pat., 2007013 (1935).
7 Wei, D., Jiang, H., Jing, X., Yuan, J., “Measurement and correlation of solubilities of 4-hydroxybenzaldehyde and its bromo-derivatives in chloroform”,.... (), 55, 1192-1195 (2004). (in Chinese)
8 Paladi, F.G., Gamurari, V.J., Oguni, M., “Effect of annealing in glass-transition region on anomalous generation and extinction of crystal nuclei at very low temperatures in o-benzylphenol and salol”,..., 1, 64-68 (2002).
9 Lide, D.R., CRC Handbook of Chemistry and Physics: A Ready-reference Book of Chemical and Physical Data, 86th edition., Taylor & Francis, London (2005).
10 Jin, K., Wei, D., Li, H., “Solid-liquid equilibria of the isomers of tetramethyl benzene”,.., 62-69 (1991). (in Chinese)
11 Hanaya, M., Hikima, T., Hatase, M., Oguni, M., “Low-temperature adiabatic calorimetry of salol and benzophenone and microscopic observation of their crystallization: finding of homogeneous-nucleation- based crystallization”,.., 34, 1173-1193 (2002).
12 Gatta, G.D., Richardson, M.J., Sarge, S.M., Stølen, S., “Standards, calibration, and guidelines in microcalorimetry Part 2. Calibration standards for differential scanning calorimetry (IUPAC Technical Report)”,.., 78, 1455-1476 (2006).
13 Richert, R., Angell, C.A., “Dynamics of glass-forming liquids. V. On the link between molecular dynamics and configurational entropy”,..., 108, 9016 (1998).
14 The Chemical Database of the University of Akron, http://ull.chemistry.uakron.edu/erd/ chemicals/8001/8324.html (2008).
15 Gmehling, J., Onken, U., Arlt, W., Vapor-Liquid Equilibrium Data Collection. Pt. 2b, Organic Hydrocxy Compounds: Alcohols and Phenols, DECHEMA, Frankfurt (1978).
16 Fredenslund, A., Gmehling, G., Rasmussen, P., Vapor-Liquid Equilibria Using UNIFAC, Elsevier, Amsterdam (1977).
17 Prausnitz, J.M., Lichtenthaler, R.N., Gomes de Azevedo, E., Molecular Themodynamics of Fluid-phase Equilibria, 3rd edition, Prentice-Hall PTR, Englewood Cliffs (1999).
18 Wilson, G.M., “Vapour-liquid equilibrium XI: A new expression for the excess free energy of mixing”,...., 86, 127-130 (1964).
19 Renon, H., Prausnitz, J.M., “Local compositions in thermodynamic excess functions for liquid mixtures”,., 14, 135-144 (1968).
20 Abrams, D.S., Prausnitz, J.M., “Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems”,., 21, 116-128 (1975).
2008-09-04,
2008-11-03.
* To whom correspondence should be addressed. E-mail: weidwei@tju.edu.cn
 Chinese Journal of Chemical Engineering2009年1期
Chinese Journal of Chemical Engineering2009年1期
- Chinese Journal of Chemical Engineering的其它文章
- Modeling and Optimization for Scheduling of Chemical Batch Processes*
- Simulation of Droplet-gas Flow in the Effervescent Atomization Spray with an Impinging Plate*
- Numerical Investigation of Constructal Distributors with Different Configurations*
- The Kinetics of the Esterification of Free Fatty Acids in Waste Cooking Oil Using Fe2(SO4)3/C Catalyst
- Multiple Model Soft Sensor Based on Affinity Propagation, Gaussian Process and Bayesian Committee Machine*
- Steam Reforming of Dimethyl Ether over Coupled Catalysts of CuO-ZnO-Al2O3-ZrO2 and Solid-acid Catalyst*
