Multiple Model Soft Sensor Based on Affinity Propagation, Gaussian Process and Bayesian Committee Machine*

LI Xiuliang (李修亮), SU Hongye (苏宏业)** and CHU Jian (褚健)



Multiple Model Soft Sensor Based on Affinity Propagation, Gaussian Process and Bayesian Committee Machine*

LI Xiuliang (李修亮), SU Hongye (苏宏业)** and CHU Jian (褚健)

National Key Laboratory of Industrial Control Technology, Institute of Cyber-Systems and Control, Zhejiang University, Hangzhou 310027, China

Presented is a multiple model soft sensing method based on Affinity Propagation (AP), Gaussian process (GP) and Bayesian committee machine (BCM). AP clustering arithmetic is used to cluster training samples according to their operating points. Then, the sub-models are estimated by Gaussian Process Regression (GPR). Finally, in order to get a global probabilistic prediction, Bayesian committee machine is used to combine the outputs of the sub-estimators. The proposed method has been applied to predict the light naphtha end point in hydrocracker fractionators. Practical applications indicate that it is useful for the online prediction of quality monitoring in chemical processes.

multiple model, soft sensor, affinity propagation, Gaussian process, Bayesian committee machine

1 INTRODUCTION

Soft sensors are prerequisite to the immeasurable quality indicator monitoring and control in chemical processes. The operating variables are held at the set point nearby when chemical process operating is at normal production state. Occasionally, the production needs switch work mode (or named operating point). In such case, the historical samples are clustered around different operating points. The usual approach in order to get a clear description of the production process character is to collect historical samples as many as possible. But samples near different work modes display dissimilar properties in disturbance range and nonlinear properties. So the single mode1 for complex system does not work any longer, because it caused lower estimation precision and over-fitting problems [1].

To overcome the aforementioned difficulties, multiple model (MM) has been advocated by some researches for complex processes. Multiple model involves several submodels and its global output is generated with the weighted sum of submodels outputs.

Figure 1 Framework of multiple model soft sensor

However, the following drawback has appeared in practice. (1) The samples can not be effectively clustered to reflect the different work models. One of the main reason is that the second variables have the same weight factors in clustering model. The other reason is that the number of the sub-clusters is usually fixed by priori and the model can not track the movement of work points. (2) The combining method based on fuzzy membership in FCM is not suitable in practice, because the weight factor should be based on the degree of prediction confidence. (3) The output is not a probabilistic distribution prediction. Currently, the sub-estimators are modeled by point estimation technique, such as TS, ANN and SVR, so we can not assess the confidence and distribution of the prediction.

In this article, a multiple model soft sensor method is proposed. Like traditional MM soft sensor, it also consists of three distinct steps. In the first step, with affinity propagation (AP) clustering method [8], the training samples are clustered in according to the different work modes. In the second step, sub-models are estimated with Gaussian process regression [9, 10] which provides a probabilistic non-parametric modeling approach. And in the final step, Bayesian committee machine is used to combine the estimators of sub-models and generate the global probabilistic distribution prediction.

2 AFFINITY PROPAGATION

Clustering based on a measure of similarity is a crucial problem which appears throughout scientific data analysis. Recently, a powerful algorithm called affinity propagation (AP) based on message passing technique was published in Science by Frey and Dueck [8]. Affinity propagation has fast processing speed and can avoid many of the poor solutions which caused by unlucky initializations and hard decisions.

2.1 Principle and algorithm of affinity propagation

Affinity propagation is based on similarities(,) (or×similarity matrixfordata points) between pairs of data points, and simultaneously considers all the data points as potential cluster centers (called exemplars). To find appropriate exemplars, AP accumulates evidence “responsibility”(,) from data pointfor how well-suited pointis to serve as the exemplar for point, and accumulates evidence “availability”(,) from candidate exemplar pointfor how appropriate it would be for pointto choose pointas a final cluster center. Based on evidence accumulation, AP searches for clusters through an iterative process until a high-quality set of exemplars and corresponding clusters emerges. The algorithm is as follows:

(1) Input:,,

(3) Responsibility updates:

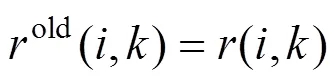
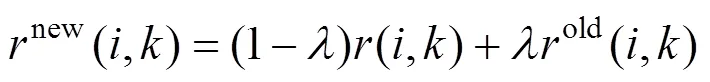
(4) Availability updates:

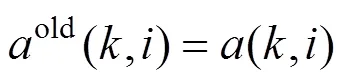
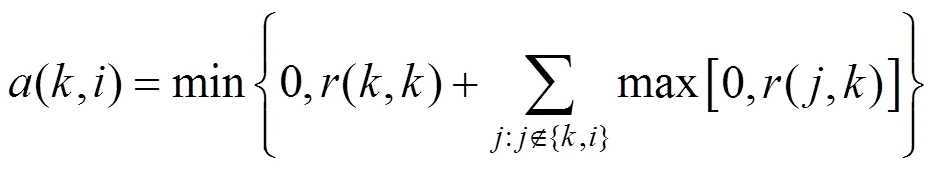
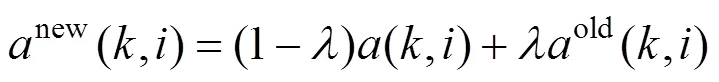
(5) Iterative from step 3 and step 4 until a high- quality set of exemplars and corresponding clusters emerges. Then go to step 6.

(6) Making assignments:

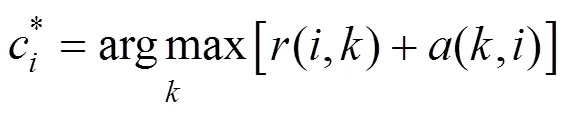
2.2 Parameter of affinity propagation

There are three important parameters in AP:,,.

Before the similarityis calculated, the datamust be normalized with Eq. (9) to overcome the dimension effect of different second variables.

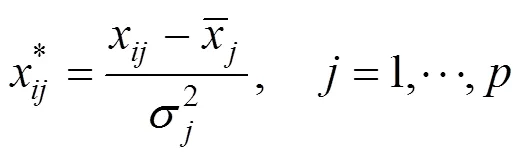
As the goal of soft sensor is to minimized squared error, each similarity(,) is set to a negative squared error (Euclidean distance):

wis the weight factor of second variables. It can be estimated according to the important degree of second variables to work modes by technologist and adjust in practice.

The preferences(its initial value is negative) is used in diagonal of similarity matrixand indicates the preference that data pointshould be chosen as a cluster center, it influences the number of clusters. And usually a good choice is to set all the() to the median of(exclude its diagonal). However this choice can not lead to an optimal clustering solution in the new multiple model soft sensor method, so we set

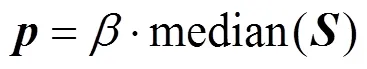
can be adjusted in according to special applications.

3 GAUSSIAN PROCESS REGRESSION

Gaussian process (GP) is a flexible, probabilistic and non-parametric model [8, 9]. From function view, GP is a collection of random variables which have a joint multivariate Gaussian distribution [9]. Gaussian process has a property that examination of a larger set of variables does not change the distribution of the smaller one [9]. So through the clustering method and GPR, we can implement the incremental learning and get probabilistic prediction. With the presented MM soft sensor, we can gain knowledge of the different work modes with the assumptions of the dissimilar propertyprior in disturbance range and nonlinear character.

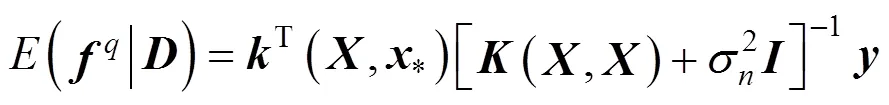
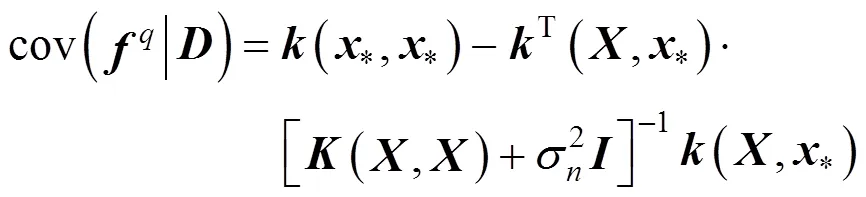
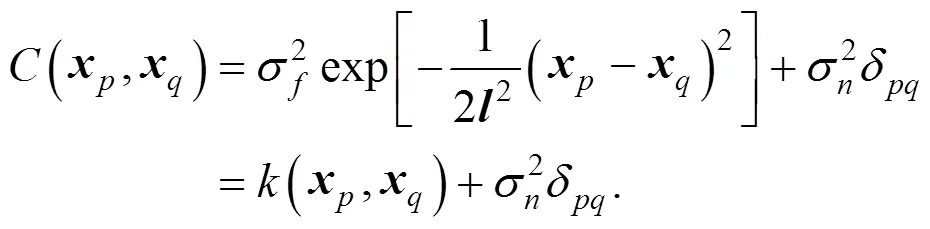
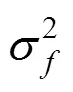
4 BAYESIAN COMMITTEE MACHINE

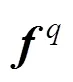
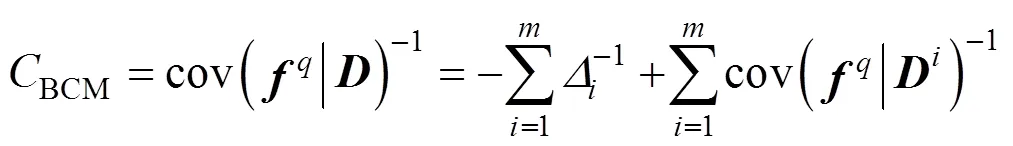
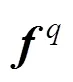
5 PERFORMANCE EVALUATION INDICATOR

Generally, we use root mean square error [RMSE, Eq. (18)] as the indicator to evaluate the error of model. But they are impacted by the dimension value of the output, so they are not suitable to estimate the tracking precision between the prediction and the measurement value.

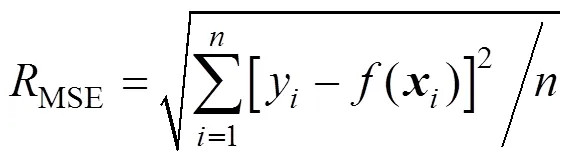
In order to overcome the effect of dimension, we introduce a new indicators to evaluate tracking precision: relative variance tracking precision [13] (RVTP) Eq. (19).

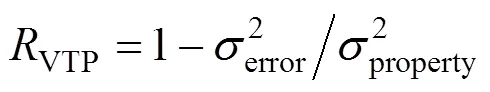
6 CASE STUDIES

6.1 Simulation and analysis

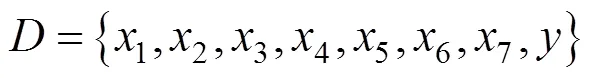
In AP+GP+BCM method, the AP clustering weight factor in Eq. (10) is set to [1.59, 1.52, 0.98, 0.33, 0.63, 0.78, 0.31] and weight factorin Eq. (11) is set to 65.

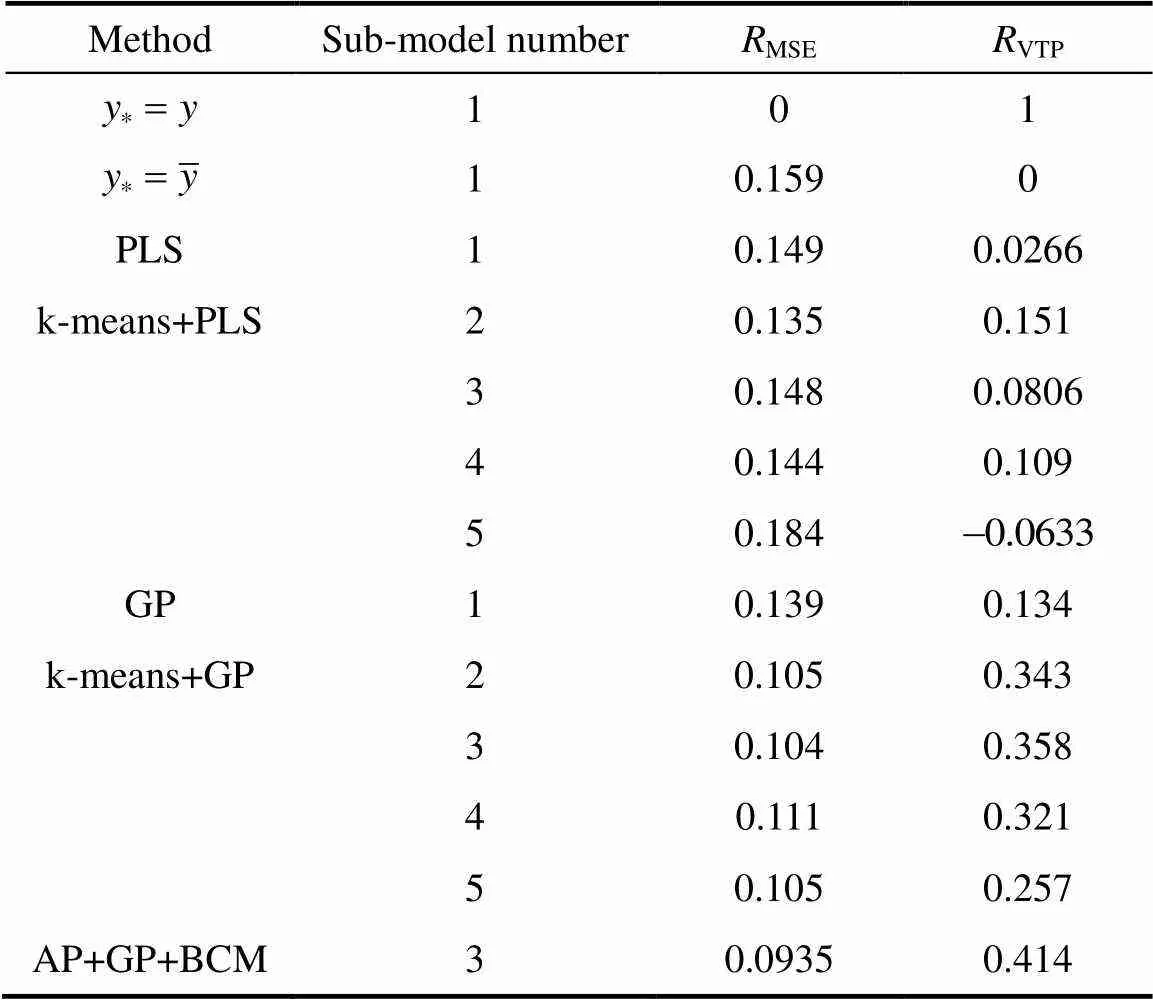
Table 1 Simulation result

Partial least squares (PLS) and k-means PLS method are observed. They have lower accuracy than those of nonlinear models, implying that nonlinear methods are better than linear one for debutanizer column.

Noting the k-means method, most of them have better performance than the global model. It means that multi-model methods outperform single global model. The performance of k-means methods are determined by the number of clusters which is set a priori.

See the AP+GP+BCM method proposed in this article. It gives a Gaussian distribution prediction and shows the best performance. The clustering distance weighted factor is determined by their relativity to the work modes and the number of sub-models is determined automatically.

6.2 Application and results

In hydrocracker fractionators process, the immeasurable quality indicator is the light naphtha end point (95% distillation range) and should be strictly monitored and controlled. The end point can be offered by artificial laboratory per eight hours. Its prediction is one of the most difficult tasks in industrial process field. We apply the proposed MM soft sensor to estimate it.

According to mechanism analysis and experience in practice, we choose ten second variables: feed temperature, feed flow rate, temperature of the fractionator top, reflux ratio of the fractionator top, temperature of the reflux jar on the fractionator top, temperature of cutpoint of heavy naphtha, temperature of cut point of diesel,temperature of the middle reflux, flow rate of the middle reflux and temperature of the fractionator bottom. The output variable is the end point of light naphtha.

Data collected in plant database is generally corrupted by the presence of outliers and noise, and the data inconsistent with the majority of recorded data can greatly affect the performance of data driven soft sensor design. Here, we used three steps to prepare the data for soft sensor. First, the strategy of 3edit rule [14] is used to detect outliers. In 3edit rule, the normalized distancedis computed:

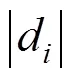
The application result can be seen in Fig. 2. With the multiple model soft sensor based on AP, GPR and BCM, we obtain not only the prediction value but also the prediction variance with confidence. In other words, we get a Gaussian distribution prediction with confidence. The result shows that the multi-model soft sensor method has a good tracking precision performance and can guide production better.

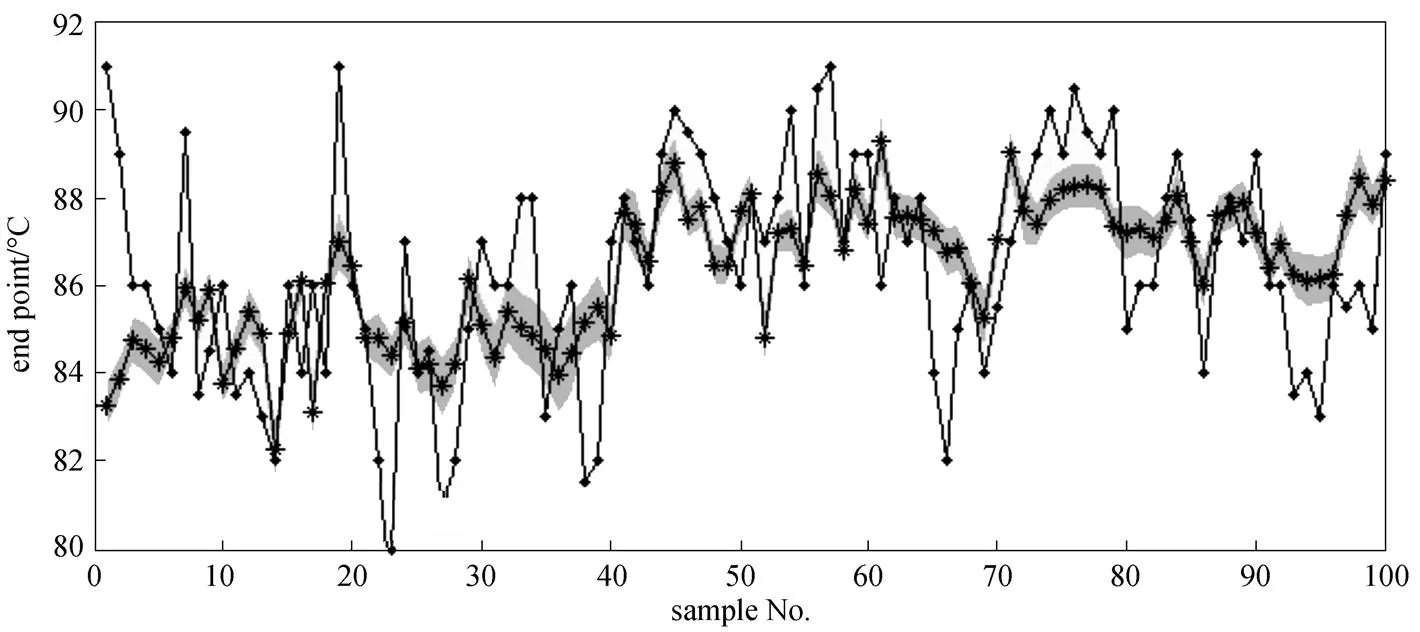
Figure 2 Applications result of multiple model soft sensor based on AP+GP+BCM

7 CONCLUSIONS

In this article, a multiple model soft sensor algorithm is proposed. The algorithm is comprised of three steps. First, AP clustering arithmetic is used to cluster the training samples according to different work modes. Second, GPR is used to build a nonlinear model for each sub cluster and gives Gaussian distribution predictions. Third, the Gaussian predictions are combined by Bayesian committee machine. The simulation results show that it is superior to the soft sensor based on sliding window or traditional multiple model soft sensor.

1 Liu, J.L., “On-line soft sensor for polyethylene process with multiple production grades”,, 15, 769-778 (2007).

2 Feng, R., Zhang, Y.Z., Song, C.L., Shao, H.H., “A multiple model approach to modeling based on fuzzy support vector machines”,, 8 (2), 137-141 (2003).

3 Zhang, Y., Li, N., Huang, D., “Soft sensor of polyester reaction based on multiple neural network model”,(), 31 (2), 208-211 (2005).

4 Gui, W.H., Li, Y.G., Yang, C.H., Chen, Z.S., “Distributed SVM based on improved clustering algorithm and its application”,, 19 (8), 852-856 (2004).

5 Du, W.L., Qian, F., Liu, M.D., Zhang, K., “4-CBA soft sensor based on fuzzy CMAC neural networks”,...., 13 (3), 437-440 (2005).

6 Zhang, Y., Su, H.Y., Liu, R.L., Chu, J., “Fuzzy support vector regression model of 4-CBA concentration for industrial PTA oxidation process”,...., 13 (5), 642-648 (2005).

7 Wang, J.L., Yu, T., Jin, C.Y., “On-line estimation of biomass in fermentation process using support vector machine”,...., 14 (3), 383-388 (2006).

8 Frey, J., Dueck, D., “Clustering by passing messages between data points”,, 315 (5814), 972-976 (2007).

9 Rasmussen, C.E., Williams, C.K.I., Gaussian Process for Machine Learning, MIT Press, USA, 8-31(2006).

10 Likar, B., Kocijian, J., “Predictive control of a gas-liquid separation plant based on Gaussian process model”,..., 31, 142-152 (2007).

11 Tresp, V., “A Bayesian committee machine”,, 12, 2719-2741 (2000).

12 Tresp, V., “The generalization Bayesian committee machine”, In: Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, NY, USA, 130-139 (2000).

13 King, M.J., “How to lose money with inferential properties”,, 83 (10), 47-52 (2004).

14 Fortuna, L., Graziani, S., Rizzo, A., Xibilia, M.G., Soft Sensors for Monitoring and Control of Industrial Processes, Springer Verlag, London (2006).

15 http://www.springer.com/engineering/robotics/book/978-1-84628-479-3

16 Schladt, M., Hu, B., “Soft sensors based on nonlinear steady-state data reconciliation in the process industry”,, 46, 1107-1115 (2007).

2007-08-12,

2008-10-14.

the National High Technology Research and Development Program of China (2006AA040309) and National Basic Research Program of China (2007CB714000).

** To whom correspondence should be addressed. E-mail: hysu@iipc.zju.edu.cn