基于SMA阻尼器的长拉索系统振动控制研究*

刘爱荣，禹奇才，袁向荣，谢盛奋

(广州大学土木工程学院，广东 广州 510006)

长拉索是索支撑体系结构的重要受力构件，但由于其柔度大、质量小和阻尼低等特点，在风、雨、地震、车辆等荷载作用下极易发生振动，激烈的振动会引起拉索的疲劳损伤破坏、拉索之间的碰撞破坏，从而导致拉索失效[1-4]。因此，对长拉索的振动必须加以控制。

长拉索自身的阻尼过小是产生大幅振动的一个重要原因，在拉索上合理安装耗能阻尼器是控制其大幅振动的有效手段之一。目前，利用粘弹性材料、粘滞流体等材料开发的阻尼器与拉索复合在一起组成阻尼器—拉索减振系统，取得了明显的减振效果，已被应用于工程结构中。然而，此类阻尼器在工程中应用尚需克服诸如疲劳、老化、力学性能退化及流体阻尼器可能存在的渗漏现象等问题[5-8]。因此，开发优质材料阻尼器对控制长拉索振动具有非常重要的意义。

近年来，智能材料的发展引起了人们高度重视，形状记忆合金(SMA)是近年来开发出来的一种新型智能材料，它不仅具有很高的机敏度和驱动力，而且在高温下的超弹性及低温下的形状记忆效应都具有高阻尼的特性，并且具有抗疲劳性好、耐腐蚀强、可恢复变形大及性能稳定等优点，避免了其它材料阻尼器的一些缺陷，运用到拉索的振动控制上，可以抑制索的大幅振动，确保拉索系统的耐久性，从而增加了索支撑结构的安全可靠性[9-12]。关于拉索系统或阻尼器-拉索系统的非线性振动问题已经有学者进行了大量研究，但关于拉压型SMA阻尼器-长拉索复合系统的非线性振动问题的理论与试验研究目前还比较少见。

1 SMA 拉压型阻尼器的设计

本文设计的拉压型SMA阻尼器由超弹性形状记忆合金丝、拉杆、螺钉、夹片、上盖、下盖、外筒、活塞、固定杆等部件组成，设计简图如图1示，实物相片如图2示。其中，SMA丝为西安赛特特种金属有限公司生产的等原子比NiTi合金丝，其直径为1.00 mm，有效长度35 cm，化学成分为Ni55.86%、Ti43.64和V0.5%(原子分数)，由于NiTi合金丝不能承受压力，所以SMA-阻尼器在工作之前，需对NiTi合金丝进行张拉，使其产生一定的预应变。

SMA-阻尼器拉杆的一端与活塞固定连接，另一端穿过上盖预留中心孔与螺钉、夹片连接。为了固定SMA丝，在阻尼器圆形活塞、上盖与下盖的外边缘处均匀设置了8个NiTi合金丝孔，每一丝孔固定两根SMA丝，SMA丝由螺钉固定在丝孔周围，活塞与上盖和下盖通过NiTi合金丝被连接在一起。为了方便观测活塞的定位与SMA的张拉作用，在外筒的中间位置对称开设两个观察孔，如图1、2所示。

图1 SMA-阻尼器结构示意图

拉压型SMA-阻尼器的基本工作原理是：当拉杆受拉(压)时，带动了活塞的移动，使得锚固在下盖处的NiTi合金丝受拉(压)，而锚固在上盖处的NiTi合金丝受压(拉)，形成拉力差，与拉杆的拉(压)力抵消。NiTi合金丝在被反复拉压过程中(由于NiTi合金丝有一定的预应变，事实上是不会受压的)，由于NiTi合金丝的超弹性性能，高阻尼性能得到了充分的发挥，使得力与位移间形成了饱满的滞回环，从而达到了耗能的作用。

图 2 SMA-阻尼器照片

2 SMA 拉压型阻尼器的特征参数

为了进一步了解SMA阻尼器的特性，特定义了以下基本特征参数：①等效割线刚度KS；②单位循环消耗能量WC；③等效阻尼比ξa；④阻尼系数Cv:

,,

(1)

上式中WC为单位循环耗能量，即在单次循环中由阻尼力与位移围成的面积；Fmax为单次加卸载循环中的最大输出力；Fmin为单次加卸载循环中的最小输出力；Umax为单次加卸载循环中的最大位移；Umin为单次加卸载循环中的最小位移；U为滞回环的位移幅值；ω为加载频率。

为了获得SMA-阻尼器初始应变、最大位移行程与WC、KS和ξa间的关系，特进行了以下试验。试验是在室温(24～25℃)，即加载温度大于NiTi合金奥氏体相变完成温度(8℃)，NiTi合金完全处于超弹性状态下进行的，阻尼器的加载速率为36 mm/min。试验分为两个大工况：1)位移行程幅值为7mm(相当于SMA丝长度的2%)下，NiTi合金丝的预应变值分别为2%、2.5%、3%、3.5%、4%、4.5%、5%；2)NiTi合金丝的预应变为3.5%，位移行程幅值为1.75、3.5、5.25、7和8.75。

从表1可以看出，SMA阻尼器在预应变相同的情况下，随着阻尼器位移行程的增大，阻尼器的等效刚度逐渐减小，而单位耗能量则逐渐增加，等效阻尼比在小位移情况下，随着位移的增大也逐渐增大，但当位移值达到5.25 mm(相当于丝长的1.5%)后，等效阻尼比基本保持不变。

表1 不同位移幅值和预应变下SMA阻尼器特征参数

表1亦说明，SMA阻尼器在最大位移行程一定的情况下，随着阻尼器预应变的增大，阻尼器的等效刚度逐渐变小，而阻尼器的耗能与等效阻尼比则逐渐增加，当预应变大于3.5%后，阻尼器的单位耗能量基本不变。所以综合等效刚度、耗能量和等效阻尼比的变化规律，施加于SMA阻尼器的预应变以3.5%为宜。

3 SMA阻尼器-拉索系统振动微分方程

设y0(x)为在重力荷载作用下的平衡状态下的拉索曲线的方程表达式，y(x,t)为拉索振动时的运动曲线方程表达式，在距拉索端x0处安装SMA阻尼器。

在外荷载激励下，SMA阻尼器-拉索系统的动能T、弹性应变能U分别为[8]，

在正规药店购买杜仲粉和甘草，过20目筛，根据1∶10的比例加入90-100℃的水保持恒温30min，浸提次数为两次，用8层纱布过滤去渣，滤液在60℃烘箱中浓缩至粘稠状，放入真空冷冻干燥器，冷冻至完全干燥，在4℃冰箱中贮存备用。

(2)

(3)

(4)

上式中，l为拉索计算跨径；A为拉索的面积；g为重力加速度。

设激励荷载对拉索系统做的总虚功为：

δW=δWSMA+δWC+δWP

(5)

δWSMA、δWC和δWP分别为SMA阻尼器、拉索系统阻尼力和外力做的虚功，其中[1]，

(6)

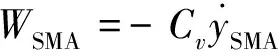
(7)

采用分离变量法，可将y(x,t)用模态坐标表示为：

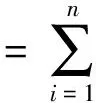
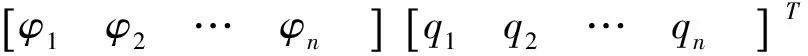
(8)

则，

φi(xC)·qi(t)=

(9)

上式中，φi(x)为拉索振动位移的形函数向量；qi(t)为拉索的广义位移坐标向量。

(10)

根据Hamilton原理，由式(5)，并对式(2)、(3)取变分，得

(11)

(12)

其中，

φiφjdx

(13)

(14)

(15)

(16)

4 SMA阻尼器对长拉索振动的影响

为了验证SMA阻尼器对长拉索振动控制效果，以某斜拉桥长拉索的缩尺模型为例，在距拉索固定端0.08 L或0.16 L(L为拉索长度)处垂直拉索安装一SMA阻尼器，如图3。索的初始张拉力为800 N，在拉索的跨中处施加1.0 cm的初始位移激励。

图3 SMA阻尼器-拉索试验系统

通过试验测试得出拉索在未安装SMA阻尼器时的模态阻尼比为1.54%，而在0.16 L处安装阻尼器后为5.11%。图4(a)和5(a)分别为拉索系统未安装SMA-阻尼器(无控)的加速度和位移响应时程；图4(b)和5(b)分别为拉索系统在0.16 L处安装了SMA-阻尼器(有控)的加速度和位移响应时程。从图4和图5可以看出，安装了SMA阻尼器后拉索跨中处的位移和加速度响应的幅值均有减小，且位移和加速度的衰减速度大幅度提高，说明本文所设计的SMA-阻尼器的耗能能力强，对长拉索的振动有较好的控制效果。

图4 拉索有控和无控时加速度时程反应

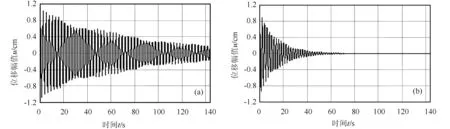
图5 拉索无控和有控时位移时程反应

图6给出了当SMA阻尼器位于0.08 L处时长拉索加速度时程的试验值和理论计算值，二者基本吻合，表明上述理论推导是正确的。

5 结 论

通过以上研究，可得出以下结论：

图6 拉索加速度时程响应的试验值和理论值的比较

(1)本文所设计的SMA阻尼器具有高阻尼性能，对拉索结构具有明显的耗能与减震效果，可以有效减少拉索的振动位移以及加速度幅值，并且大幅度提高了振动衰减速度。

(2)在位移行程一定的情况下，随着阻尼器预应变的增大，阻尼器的等效刚度逐渐减小，而阻尼器的耗能与等效阻尼比则逐渐增加，当预应变大于3.5%后，阻尼器的单位耗能量基本不变。所以综合等效刚度、耗能量和等效阻尼比的变化规律，施加于SMA阻尼器的预应变以3.5%为宜。

(3)SMA阻尼器在预应变相同的情况下，随着阻尼器位移行程的增大，阻尼器的等效刚度逐渐变小，而单位耗能量则逐渐增加，等效阻尼比在小位移情况下，随着位移的增大也逐渐增大，但当位移值达到一定量值后，等效阻尼比基本保持不变。

(4)SMA阻尼器-拉索系统的加速度时程响应的试验与理论值基本吻合，说明本文理论推导是正确的。

参考文献：

[1] 谢盛奋．长拉索的振动分析及应用形状记忆合金进行减振控制试验研究[D]．广州大学硕士学位论文，2008.

XIE S F. Experimental study on long cable vibration analysis and application of shape memory alloy to reduce vibration control [D]. Master Dissertation of Guangzhou University,2008.

[2] YAMAGUCI H H, NAGAHAWATTAL H D. Damping effects of cable ties in cable-stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995,54:35-43.

[3] HIKAMI Y, SHIRAISHI N. Rain-wind induced vibration of cables in cable stayed bridges[J].Journal of Bridge Engineering, 1998,29:409-418.

[4] YAMAGUCHI H，Alauddin M. Control of cable vibrations using secondary cable with special reference to nonlinearity and interaction[J]. Engineering Structures,2003,25:801-816.

[5] XU Y L, YU Z. Vibration of inclined sag cables with oil dampers in cable-stayed bridges[J].Journal of Bridge Engineering, 1998,3(4):194-203.

[6] 胡建华，王修勇，陈政清，等.斜拉桥拉索磁流变阻尼器减振技术的参数优化研究[J].土木工程学报，2006，39(3)：91-97.

HU J H,WANG X Y,CHEN Z Q,et al.Parametric optimization formitigatign cable vibration by using MR dampers on cable-stayed bridges[J]. China Civil Engineering Journal,2006,39(3):91-97.

[7] 王修勇，陈政清，何旭辉，等.斜拉桥拉索风雨振控制的智能阻尼技术[J].振动与冲击，2002，21(3):26-30.

WANG X Y,CHEN Z Q, HE X H, et al. Control of wind-rain-Induced vibration of staty cables on cable-stayed bridge using smarted damping[J].Journal of Vibration and Shock,2002,21(3):26-30.

[8] 王修勇. 斜拉桥拉索振动控制新技术研究[D].长沙：湖南大学博士学位论文,2002.

WANG X Y. Study of new techniques for suppressing cables vibration on the cable-stayed bridges[D]. Doctor Dissertation of Hunan University 2002.

[9] MAURO D, DONATELLO C, ROBERT M. Implementation and testing of passive control devices based on shape memory alloys[J].Earthquake Engineering Structural Dynamics, 2000，29(2)：945-968.

[10] VHAN Y L, LI Q S, LI A Q, et al. Structural vibration control by shape memory alloy damper[J].Earthquake Engineering & Structural Dynamics, 2003，32：483-494.

[11] 李惠，刘敏，欧进萍．斜拉索-形状记忆合金耗能减振系统动力特性和模态分析[J]．振动工程学报，2005，18(1)：64-69.

LI H, LIU M, OU J P. Dynamic properties and modal response analysis of stay cable attached with SMA damper[J]. Journal of Vibration Engineering, 2005,18(1):64-69.

[12] 王社良，苏三庆，沈亚鹏.形状记忆合金拉索被动控制结构地震响应分析[J].土木工程学报,2000,33(1):56-62.

WANG S L, SU S Q, SHEN Y P. Seismic response analysis for passive structural control with shape memory alloy tendons[J].China Civil Engineering Journal, 2000,33(1):56-62.