“探索直角三角形全等的条件”课例设计

翟　芸　刘　勇

一、设计理念

思维导图作为一种思维工具，在我国的应用还处于起步阶段。此教学课例以创造性思维的六要素结构理论为指导，教师利用多媒体创设问题情境，激发学生想象，引导学生思考，让学生利用思维导图探索直角三角形全等的条件，给学生充分发挥的自由空间，从而有效地培养了学生的发散思维、直觉思维、形象思维、逻辑思维、辩证思维，进而促使其创造性思维得到充分发展。

二、教学内容

此教学课例选取山东省教育出版社2005年出版的初中一年级《数学》教科书下册中“探索直角三角形全等的条件”为教学内容。

三、教学目标

知识目标：掌握已知斜边、直角边画直角三角形的画图方法；掌握斜边、直角边公理（HL）。

能力目标：通过尺规作图使学生得到技能的训练；培养学生分析、比较等数学思维方法；通过逻辑思维、发散思维、直觉思维、形象思维、辩证思维等的培养来开发学生的创造性思维。

情感目标：培养学生学习数学的兴趣；培养学生用科学的方法去探索数学真相、数学规律的态度与情感。

四、教学重点、难点

教学重点：探求斜边、直角边公理的过程以及在此过程中学生创造性思维的培养。

教学难点：以具体的情景环境为切入点，引导学生探究式学习的过程，以及如何引导学生对各知识点之间的内在联系进行反思，以便构建完整知识体系。

五、教学准备

学生具备知识：能熟练应用Word 2003制作思维导图，并基本掌握三角形全等的概念、判定条件、性质等知识。

教学环境与资源：已安装电子教室软件的多媒体教室，教师机能对每台电脑进行控制，每台电脑均安装Word 2003。用Flash制作一个舞台背景课件。

实物：黑板、直尺、三角板、圆规、铅笔、白纸等。

六、教学过程

（一）创设问题情境

教师通过多媒体课件向学生展示一个舞台背景。舞台背景的形状是由两个直角三角形组成，每个三角形都有一条直角边被花盆遮住。

多媒体课件展示问题一：如果想知道这两个直角三角形是否全等，该怎么办？

师：每个三角形都有一条直角边被花盆遮住，无法测量。请同学们利用自己所学的知识，想一想如何判断这两个直角三角形是否全等。

设计意图：利用多媒体创设问题情景，能更好地激发学生的学习兴趣，有利于教学活动的进一步发展。

（二）利用思维导图探求解决问题的途径

教师让学生每4人组成一个学习小组。小组内成员展开讨论。根据讨论的结果，画出自己解决问题的思维导图，限时10分钟。学生们积极地展开讨论，当他们听说要用思维导图画出自己的想法时，都很感兴趣。

教师巡视学生的作图情况，并选取典型答案通过电子教室给予讲解。下面是两位同学的思维导图，从此思维导图中，我们可以清晰地看出他们求解问题答案的思维过程。

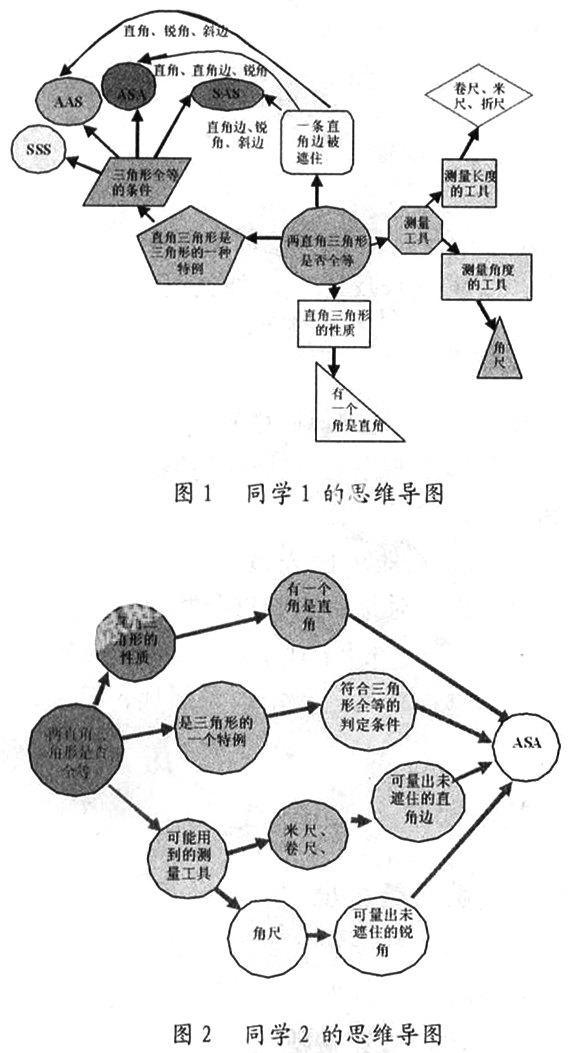
（三）问题继续深入

师：如果不能用角尺来测量角的度数，只能用卷尺测量未遮住的直角边和斜边的长度，能确定两个直角三角形全等吗？

学生以小组为单位展开讨论，再修改自己的思维导图，限时5分钟。在此环节中，有的学生显得无从下手。他们认为，只有两个边无法判断两个三角形是否全等（此类学生忘记直角三角形有一个直角的本质属性）。有的学生想到了直角（这样很好），由他们的思维导图得出了边边角SSA定理，这与前面学习的三角形全等判定条件不符，他们开始怀疑。下面是同学1修改后的思维导图。

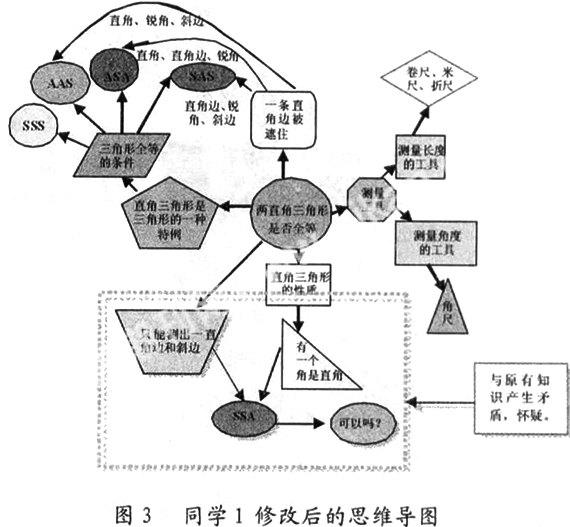
设计意图：此环节中，学生产生了质疑，与已有知识产生冲突，思维处于矛盾状态，需要教师的正确引导。虽然质疑并不是每次都对问题有创新性的见解,或将疑问进行创造性解决，但它仍不失为最有可能打开创造性之门的钥匙。教会学生自己质疑,是培养学生学习能力、激发创新思维的重要手段之一。

（四）教师适时引导，得出结论

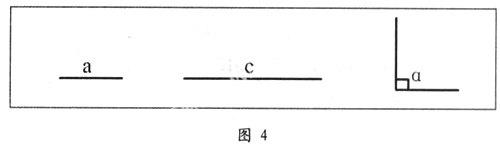
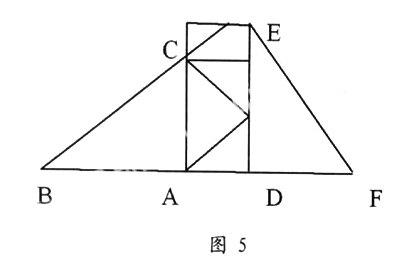
多媒体课件展示问题二：已知线段a,c（a

教师在黑板上边演示边讲解此题。学生在白纸上作图。

师：△ABC就是所求作的三角形吗？剪下这个三角形，和其他同学所作的三角形进行比较，看它们能重合吗？

同学们通过比较发现自己剪下的三角形与其他同学得到的三角形能完全重合（忽略误差）。由此得出判断直角三角形全等的另一重要判定定理：斜边和一条直角边对应相等的两个直角三角形全等，简写成“斜边、直角边”或“HL”定理。

设计意图：通过尺规作图不但使学生得到技能的训练，而且能加深对知识的理解与掌握。

（五）练习中巩固

多媒体课件展示问题三：如图5，有两个长度相同的滑梯(BC=FE)，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系？

学生得出结论：在RT△ABC和RT△DEF中，两斜边BC=EF,两直角边AC=DF,可由HL定理得到两三角形全等，故∠ABC和∠DFE互余。

设计意图：通过练习，让学生加深对HL定理的理解，并能够熟练应用。

（六）反思各知识点的内在联系，构建完整知识体系

师：你能够用几种方法说明两个直角三角形全等？

生：直角三角形是三角形的一种，判断三角形全等条件的定理也适合直角三角形全等条件的判断。那么，除了边边边定理、角边角定理、角角边定理、边角边定理可以判断直角三角形全等以外，还可以用HL定理来判断。

七、教学反思

我们从上面案例的设计与实施过程中可以看出，思维导图在开发学生创造性思维方面具有优势。思维导图的运用不仅使学生的创造性思维得到充分的开发，并且唤起一些对数学不太感兴趣的学生对数学学习的热情。

参考文献

[1]翟芸.信息技术环境下中学生创造性思维培养策略研究[D].南京师范大学学位评定委员会，2006.

[2]何克抗.论语文教育中的创造性思维培养[J].中国教育和科研计算机网.

（作者单位：山东烟台南山学院）