潜射导弹发射装置发射时的结构动力学分析
李兵尚 丁浩杰 姚 勇 冀海燕
1海军潜艇学院,山东青岛266071 2中国人民解放军91515部队,海南 三亚572016
潜射导弹发射装置发射时的结构动力学分析
李兵尚1丁浩杰1姚 勇2冀海燕1
1海军潜艇学院,山东青岛266071 2中国人民解放军91515部队,海南 三亚572016
导弹水下发射产生巨大的反冲击力,引发潜艇本体以及发射装置的强烈振动,对发射装置的结构强度、筒内导弹的安全和下一枚导弹的发射产生不可忽视的影响。基于结构动力学基本理论和有限元法,分析了系统发射时的振动特点、问题难点和外载荷情况。对潜射导弹发射装置结构动力学模型进行有限元计算做了理论分析和方法步骤的探讨,基本解决了系统建立思路问题。
潜射导弹发射装置;结构动力学;有限元法
1 引言
导弹的水下发射产生巨大的反冲击力,作用在潜艇固壳上,引起潜艇振动,特别是发射装置中发射筒的振动,对发射装置的结构强度以及其它筒内导弹的安全产生很大影响。连射时,当前的振动状态对下一发导弹的内弹道飞行产生初始扰动。水下发射时引发潜艇振动的影响因素极其复杂,对它的分析计算和控制是潜射导弹发射动力学的重要研究内容[1-4]。准确地对潜射导弹发射装置进行结构动力学分析,建立系统总体布局的结构参数与振动特性之间的定量关系,是设计系统振动频率分布的前提,可达到优化动态性能的目的。因此,对潜射导弹发射装置发射时的结构动力学特征进行分析具有十分重要的意义[5-8]。
对潜射导弹发射装置进行结构动力学研究,发射时产生的振动叠加问题以及由于发射时引起的发射装置质量分布等结构参数不对称而产生的振动耦合问题是研究的难点。本文分析了发射时发射装置的振动特点、问题难点和研究方法,探讨外载荷的特点以及如何通过载荷步施加载荷。对潜射导弹发射装置结构动力学模型进行有限元计算做了理论分析和方法步骤的探讨。
2 问题描述
对于潜射导弹发射装置,如图1所示,当水下发射导弹时,产生百吨秒以上的冲量作用在潜艇上,系统产生剧烈振动响应。这种振动有一个响应过程,属于有阻尼的衰减振动,连续发射时,该振动响应过程并未结束,这时第2枚开始发射。显然,第1枚导弹发射引起的系统振动会对第2枚导弹的内弹道飞行产生初始扰动,直接影响第2枚导弹的出筒姿态。
而第1、2枚导弹产生的系统振动响应,又会叠加到后续导弹的发射中去。当导弹连续发射时,这种叠加情况会一直连续下去。并且随着导弹数量的减少以及发射后海水涌入发射筒中使整个发射装置的质量分布等参数变得非对称分布,从而引起系统的振动耦合问题。

图1 连发时潜射导弹武器系统的结构动力学响应描述
3 问题难点
3.1 难点分析
发射动力学已有较长的历史,结构动力学研究作为潜射导弹发射装置的重要特征成为发射动力学的主要研究内容之一。综合当前研究状况,主要有3个重要问题需要解决:
1)潜射导弹发射装置作为多体系统,系统建模时含有刚体和弹性体,这增加了系统建模的复杂性,从而使系统固有振动特性的计算困难大大增加;
2)潜射导弹发射装置的载体是潜艇,潜艇处于一定深度的海水中,发射时,潜艇固壳与海水之间存在流固耦合问题,这给发射装置的建模环境增加了难度。
3)潜射导弹发射装置具有连续发射导弹的特点,此时系统的模型是变化的,外载荷不断地施加于系统模型上,这两点给系统的结构动力学分析带来很大困难[9,10]。
解决上述问题面临的主要困难有:
1)用通常的力学方法在对潜射导弹发射装置进行结构动力学分析时,模型难于建立,计算工作量大大增加,并且复杂的建模使后续的计算容易出现病态问题,需要不断修正模型,改进计算方法;
2)在研究手段上,经典的模态方法难以对此类系统的结构动力学响应问题进行精确分析。潜射导弹发射装置模型同时含有刚体单元和弹性体单元,系统特征值问题非自共轭,系统特征向量不具有通常意义下的正交性,从而给研究手段和方法提出了新的课题。
3.2 研究方法
潜射导弹发射装置属于复杂的多体系统,对其进行结构动力学分析,往往是多种研究方法的综合应用。常用的研究方法主要有模态分析法、有限元法和结构模态综合法。目前,国内在解决多体系统结构动力学问题时发展了一种新方法——多体系统传递矩阵法:建立好多体系统各元件的传递矩阵,将各元件的力学特性用矩阵表示,拼装传递矩阵中相对应元件的传递矩阵得到系统的总传递矩阵,结合边界条件得到系统的特征方程,对其进行求解即可得到系统的固有振动特性。它具有计算规模小、矩阵阶次低以及有效避免计算 “病态”等特点。其次,有限元法是当前国内外日益完善和成熟的有效方法,本文着重探讨基于有限元法的潜射导弹发射装置结构动力学模型的建立。
4 理论分析
应用有限元法对潜射导弹发射装置结构动力学模型进行振动响应分析,首先对潜射导弹发射装置三维实体模型进行结构离散,构造各单元的动能函数T(e)、势能函数W(e)和耗散能函数R(e),然后集合各单元的T(e)、W(e)和R(e)形成系统的T、W和R,即:

其中,M(e)为单元的质量矩阵,M(e)=K(e)为单元的刚度矩阵,K(e)=单元的阻尼矩阵,C(e)=;Q(e)为单元的载荷向量,M为系统的质量矩阵,K为系统的刚度矩阵,C为系统的阻尼矩阵,Q为系统的载荷向量,Δ为系统各节点的位移向量。
将式(2)代入Lagrange方程:
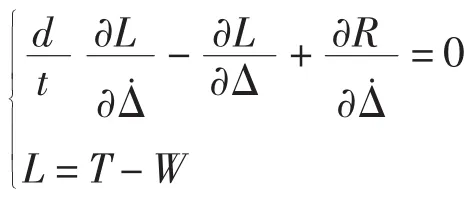
整理后,得到潜射导弹发射装置结构动力学模型运动方程的有限元形式:

解上述系统运动方程即可得到结构各节点的位移响应、速度响应、加速度响应,通过转换矩阵,可进一步求解结构各节点的动应变和动应力等。有限元求解可以通过大型工程软件来实现,利用软件的瞬态动力学分析模块确定结构在静载荷、瞬态载荷和简谐载荷的随意组合作用下的振动叠加动力响应情况,包括随时间变化的位移、应变和应力等情况。采用有限元软件分析方法,潜射导弹发射装置的结构动力学响应仿真按照模型建立、求解、仿真结果分析的步骤进行。
5 模型建立
5.1 建立潜射导弹发射装置的CSG模型
潜射导弹发射装置结构动力学仿真中,为了得到精度较高的有限元模型,达到较高的仿真度,要求发射装置的实体几何模型精度较高,所以宜采用CSG实体几何建模方法建立该多体系统的实体模型。CSG是在CAD/CAM和计算机图形处理等领域中广泛应用的一种建模方法。从图形学的角度看,潜射导弹发射装置模型最终分解成若干个简单模型的逻辑运算集合。模型的几何关系被表示为模型之间的逻辑运算,模型易于表示,提高了计算机处理模型的能力。所建发射装置CSG模型没有几何尺寸的限制,可以很好地表示模型的细节。模型的另外一个优点是易于控制,只要对部分模型的属性(位置、方向)做适当的调整,而不用重构整个模型就可以得到新的发射装置CSG模型,所以模型可扩展性好。在发射装置CSG建模过程中,应注意以下几点:
1)模型的几何因素简化符合结构动力学理论规则,所简化的因素是对潜射导弹武器系统的结构动力学特性影响较小的因素;
2)模型的形状函数易于描述,确立关键点,便于后续的有限元网格划分;
3)模型应尽可能地包含与系统有关的结构动力学信息,便于在仿真实验中探讨系统结构动力学响应的普遍性规律。
5.2 模型的有限元网格划分
按照网格总体上对称均匀、实体中两线无尖锐夹角以及划分精度满足工程需要等原则,对潜射导弹发射装置CSG模型进行有限元网格划分,建立该系统的有限元模型。同时必须给模型赋予相应的材料参数,如密度等,使模型具有现实物体的属性和特征。
6 模型求解
6.1 外载荷分析
发射过程中 (导弹受发射工质气体作用至弹尾离开发射筒口),忽略发射时横向流等外因素对潜艇及发射装置的影响[9],作用在潜射导弹发射装置模型上的外载荷主要有:掉导弹重力、工质(发射工质气体)冲击力、摩擦力(适配器与筒壁)、筒口压力场负荷、“水锤”冲击力。详细分析如下:
1)掉导弹重力。导弹开始滑离前,系统重力保持为常数,质心在发射装置中的位置不变;滑离瞬间,发射装置立即去掉一发导弹重力,质心也相应发生改变。
2)工质冲击力。滑离瞬间,工质气体压力p1作用于发射筒底部区域;随着导弹滑离,p1作用面积扩大,逐渐扩至整个发射筒内壁;至弹尾离开发射筒口,p1最终减少为零。
3)摩擦力。导弹开始滑离瞬间,适配器(设3圈)与筒壁摩擦力f为静摩擦力,力值最大;然后f变为滑动摩擦力,力值减小;随着导弹滑离,各圈适配器相继脱离发射筒,f逐渐减小;至弹尾离开发射筒口,f变为零。
4)筒口压力场负荷。在弹尾离开筒口瞬间,具有一定压力的工质气体从筒口溢出,在海水中形成气泡,气泡内的能量从气泡表面以压力波形式辐射出去,因而在发射筒口附近形成一个压力场。实验证明:此压力场正负间的压力脉动,作用在筒口外相关部件的负荷相当可观。筒口压力场负荷的研究相当复杂,可通过实验来测得此压力场的分布变化规律。
5)“水锤”冲击力。弹尾离开发射筒口瞬间,舷外海水涌入发射筒,由于发射筒内外压力差和水重力的综合作用,涌入发射筒的海水形似 “水锤”冲向发射筒底,此冲击力相当大。发射筒底部“水锤”压力实验曲线如图2所示。实验证明,“水锤”压力的第一峰值大于发射工质气体的压力峰值,对发射装置结构强度产生不可忽略的影响。

图2 发射筒底部“水锤”压力实验曲线
6.2 外载荷的施加
以上5种外载荷均为时变载荷,可通过载荷步按时间历程施加于发射装置上,以第1枚导弹发射时外载荷施加情况为例进行说明(见表1)。

表1 第1枚导弹发射时有限元软件中载荷步的设定
从上面的载荷分析中,不难看出对潜射导弹发射装置结构动力学模型进行加载,如何将载荷对时间的关系划分成为合适的载荷步是一个关键问题,图3是载荷/时间的关系曲线。在曲线上的每个“拐角”都应作为一个载荷步,第一个载荷步通常用来建立初始条件,然后指定后继的瞬态载荷及加载步选项。对于每一个载荷步,都要指定载荷值和时间值,同时还要定义载荷的类型,如载荷是按阶跃还是斜坡方式施加以及是否使用自动时间步长等。所有的初始条件都施加后,即可进入有限元求解程序,对潜射导弹发射装置模型的结构动力学响应进行求解。
6.3 仿真结果分析
潜射导弹发射装置模型的仿真结果被保存在有限元软件的结构分析结果文件中。以ANSYS工程软件为例,计算结果被保存在文件Jobname.RST中,通过软件的POST26和POST1 2个功能模块调用Jobname.RST文件,绘出节点的应力云图和位移云图,也可以直接读取求解结果中节点在三维空间中位移、应力以及应变的数据库文件。其中模块POST26用于观察模型中指定点处呈现为时间函数的结果,模块POST1用于观察在给定时间整个模型的结构动力学响应状态。通过对潜射导弹发射装置模型的仿真结果的分析,总结系统振动的特点和规律,找出系统结构强度最薄弱的环节,为系统设计提供理论依据。
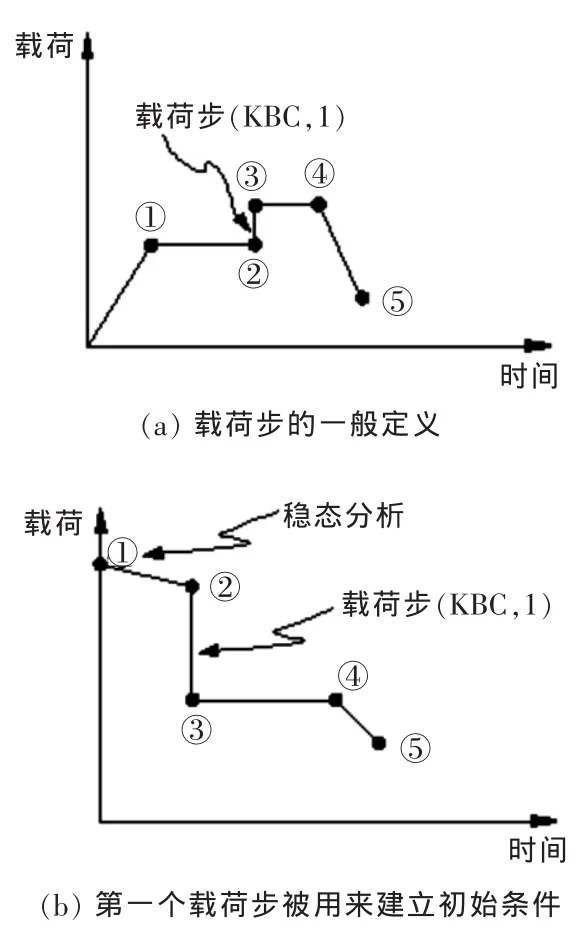
图3 载荷/时间的关系曲线
7 结论
潜射导弹发射装置为复杂的多体系统,为了不断提高该武器的作战效能和发射精度,需要进行探索性的理论研究和发射试验。本文对该问题的研究方法做了探索性的工作,分析了国内外在解决此类问题时的研究现状和研究方法以及发射时模型所受的激励因素。但这只是潜射导弹发射装置建模的框架和难点,一些问题还进行了简化处理,需要在后续的具体研发工作中去进一步地完善。
[1] 刘志勇,颜开,王宝寿.潜射导弹尾空泡从生成到拉断过程的数值模拟[J].船舶力学,2005,9(1):43-50.
[2] 淡丹辉,孙利民.结构动力有限元分析的阻尼建模及评价[J].振动与冲击,2007,26(2):121-123,137.
[3] LI BS,XU XQ.Coupled vibration analysis of multiple launch rocket system by finite element method[C].Proceedings of enhancement and promotion of computational method in Enyineering and science X,Aug,21-23,2006,Sanya,China,Springer Berlin Heidelberg,2007.
[4] 余伟炜,高炳军,陈洪军,等.ANSYS在机械与化工装备中的应用[M].北京:中国水利水电出版社,2006.
[5] 倪火才.潜地弹道导弹发射装置构造[M].哈尔滨:哈尔滨工程大学出版社,1998.
[6] 倪火才.潜射导弹水下垂直发射时的 “水锤”压力研究[J].舰船科学技术,2000,22(5):46-49.
[7] 曹嘉怡,鲁传敬,李杰,等.潜射导弹水下垂直自抛发射过程研究[J].水动力学研究与进展,2006,21(6):752-759.
[8] 程载斌,刘玉标,刘兆,等.导弹水下潜射过程的流体-固体耦合仿真[J].兵工学报,2008,29(2):178-183.
[9] 赵世平,蔡体敏.横向流对潜艇垂直发射导弹的影响[J].船舶力学,2006,10(4):33-37.
[10] 刘曜,张永,胡德斌,等.潜射导弹运载器的水弹道控制及近水面航行的稳定性分析 [J].弹箭与制导学报,2005,25(4):190-197.
Structure Dynamic Analysis on SLS When Launching
Li Bing-shang1Ding Hao-jie1Yao Yong2Ji Hai-yan1
1 Naval Submarine Academy,Qingdao 266071,China 2 Unit 91515 of PLA,Sanya 572016,China
When launching,the great power brings on acute vibration to both the submarine and the Submarine Launch System (SLS).Then the vibration has great effect on the structure intensity of the SLS,the security of missile and the launching of next missile.Based on Structure Dynamic Theory and Finite Element Method,the vibration character of the launching SLS,the difficulties and the loads are analyzed.The theoretical analysis as well as its approach and steps is also discussed as to finite element calculation of structure dynamic model for submarine missle launch system.The question of how to establish the system has been fundamentally solved.
SLS;structure dynamic analysis;finite element method
O656.3
A
1673-3185(2009)03-45-04
2008-08-04
海军装备预研项目
李兵尚(1979-),男,讲师。研究方向:兵器发射理论与技术。E-mail:667034@163.com

